机器学习-决策树算法（ID3、C4.5和CART）

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。

简介

---

决策树（Decision Tree）是⼀种树形结构，每个节点表示⼀个属性上的判断，每个分⽀代表⼀个判断结果的输出，最后每个叶节点代表⼀种分类结果，本质是⼀颗由多个判断节点组成的树。

类似if-else结构，通过若干判断（决策）来确定分类结果，比如打网球数据集中，包括天气、温度、湿度、风力四个特征，标签是play，表示是否适合打网球，属于二分类问题。

那我们便可以通过如下决策树进行预测是否适合打网球，先判断天气，再判断温度······，树中中间结点表示决策条件，叶子节点表示决策结果。

但是一个显然的问题是，我们应该如何确定判断条件的先后？比如上图中是先判断天气，若天气晴天再判断温度，再判断风力等，如果交换判断条件，将会直接影响分类结果。也就是我们需要定义划分依据，确定当前使用哪个特征值来作为划分依据，有了划分依据便可以构建决策树。划分依据包括ID3算法、C4.5算法和CART算法。

划分依据

ID3算法

---

ID3算法全称Iterative Dichotomiser 3，使用信息增益来作为划分依据，信息增益（information gain）就是划分数据集前后熵（information entropy）的差值。

物理学中，熵用来度量混乱程度。也就是说，熵越大则越乱，熵越小则越有序。我们希望决策条件划分出来的结果尽可能的属于同一类，即结点的“纯度”越来越高。

假设样本集合$D$共有$N$类，$p_k$表示样本集合$D$中第$k$类样本所占比例，$D$的信息熵$H(D)$的定义如下：

$$H(D)=-\sum _{k=1}^N{p}_{k}lo{g}_2{p}_k$$
由于比例$p_k$取值(0,1)，而log函数在(0,1)间为负，添加负号，使熵的值为正。$H(D)$的值越小，则$D$的纯度越高。
比如对于outlook特征值，14天中有5天Sunny、5天Rain、4天Overcast，则$H(outlook)=-(\frac{5}{14}lo{g}_2\frac{5}{14}+\frac{5}{14}lo{g}_2\frac{5}{14}+\frac{4}{14}lo{g}_2\frac{4}{14})=1.58$

特征$A$对数据集$D$的信息增益$G(D,A)$，定义为集合$D$的信息熵$H(D)$与特征$A$给定条件下$D$的信息条件熵$H(D|A)$之差，即：
$$Gain(D,A)=H(D)-H(D|A)=H(D)-\sum _{v=1}^V\frac{|D_v|}{|D|}H(D_v)$$

其中特征$A$有$V$个取值，即用$A$对数据集$D$来划分会产生$V$个分支，用$D_v$表示第$v$个分支中数据集$D$在特征$A$上取到第$v$个值的样本。信息增益表示得知特征X的信息⽽使得类Y的信息熵减少的程度。

比如特征$outlook$取值$sunny$时，5天$sunny$中有2天正例（yes，适合打网球），3天负例，则
$H(outloo{k}_{sunny})=-(\frac{2}{5}lo{g}_2\frac{2}{5}+\frac{3}{5}lo{g}_2\frac{3}{5})=0.97$
同理有：
$H(outloo{k}_{rain})=-(\frac{3}{5}lo{g}_2\frac{3}{5}+\frac{2}{5}lo{g}_2\frac{2}{5})=0.97$
$H(outloo{k}_{overcast})=-(\frac{4}{4}lo{g}_2\frac{4}{4}+\frac{0}{0}lo{g}_2\frac{0}{0})=0$

则特征$outloook$的信息增益$G(D,outllok)=1.58-(\frac{5}{14}\times 0.97+\frac{5}{14}\times 0.97+\frac{4}{14}\times 0)=0.24$

同样的，计算其他特征的信息增益：
$Gain(D,temp)=0.02$
$Gain(D,humidity)=0.15$
$Gain(D,wind)=0.05$
$Gain(D,outllok)$最大，所以选择$outlook$作为决策条件，根据其3个取值，将数据集$D$划分为3个数据集$D_1$、$D_2$、$D_3$，然后分别在新数据集中，计算剩余特征的信息增益，选信息增益最大的作为下一个决策条件，以此类推。当数据集全部属于一个类时，则作为叶节点，不再往下划分。
最终得到决策树如下：

但是ID3有存在缺点，总是偏向于取值更多的特征值。比如若将$day$作为特征值，则$H(day)=-(\frac{1}{14}lo{g}_2\frac{1}{14}\times 14)=3.8$
$H(da{y}_{D1})=H(da{y}_{D2})=...=H(da{y}_{D14})=-(\frac{1}{1}lo{g}_2\frac{1}{1}+\frac{0}{1}lo{g}_2\frac{0}{1})=0$
$Gain(D,day)=3.8$
即$day$的信息增益最大，因为取值多的特征值对应条件熵趋于0，导致信息增益很大，有些情况下，这些特征值并不会提供太大价值。

C4.5算法

---

C4.5算法使用信息增益率作为划分依据，避免了ID3的缺点。增益率定义为：
$$Gain\_ratio(D,A)=\frac{Gain(D,A)}{IV(A)}$$

也就是将信息增益$Gain$除以一个固定值（intrinsic value）$IV$，如果特征值的取值数目越多，则$IV$越大。
$$IV(A)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}$$

比如：
$IV(day)=-(\frac{1}{14}lo{g}_2\frac{1}{14}\times 14)=3.8$
$IV(outlook)=-(\frac{5}{14}lo{g}_2\frac{5}{14}+\frac{5}{14}lo{g}_2\frac{5}{14}+\frac{4}{14}lo{g}_2\frac{4}{14})=1.58$

C4.5算法不是直接选择增益率最大的特征，而是在信息增益超过平均增益的特征中，再筛选增益高的特征。

CART算法

---

CART（classification and regression tree）算法使用基尼指数（Gini Index）作为划分依据。

不再使用熵来定义数据集的纯度，而是使用基尼值来度量数据集纯度：
$$Gini(D)=\sum _{k=1}^N\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^N{p}_k^2$$

仍以打网球数据集$D$为例，14天中有5天不适合打网球，9天适合打网球，则数据集纯度：
$Gini(D)=1-({\frac{5}{14}}^2+{\frac{9}{14}}^2)=0.46$

基尼值反映随机抽取两个样本，其类别不一致的概率。即基尼值越小，数据集纯度越高。定义基尼指数：
$$Gini\_index(D,A)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$

若根据outlook来划分，14天中有5天Sunny（2正3负）、5天Rain（3正2负）、4天Overcast（4正0负），则：
$Gini(D_{sunny})=1-({\frac{2}{5}}^2+{\frac{3}{5}}^2)=0.48$
$Gini(D_{rain})=1-({\frac{3}{5}}^2+{\frac{2}{5}}^2)=0.48$
$Gini(D_{overcast})=1-({\frac{4}{4}}^2+{\frac{0}{4}}^2)=0$
$Gini\_index(D,outlook)=\frac{5}{14}\times 0.48+\frac{5}{14}\times 0.48+\frac{4}{14}\times 0=0.34$

同理，算其他特征的基尼指数：
$Gini\_index(D,temp)=\frac{4}{14}\times 0.5+\frac{6}{14}\times 0.44+\frac{4}{14}\times 0.35=0.431$
$Gini\_index(D,humidity)=\frac{7}{14}\times 0.49+\frac{7}{14}\times 0.24=0.365$
$Gini\_index(D,wind)=\frac{8}{14}\times 0.375+\frac{6}{14}\times 0.5=0.429$

也就是说，选择基尼指数最小的$outlook$特征作为决策条件，然后划分新数据集，往下迭代。

CART全称为分类和回归树，还可以实现回归任务，将基尼指数换成误差平方和，最后预测值与真实值满足一定误差内便可接受。因为一个特征的纯度越高，则方差越小，表示分布集中，即每次选择误差平方和最小的特征作为决策条件即可，照葫芦画瓢，不再赘述。

上述3种算法都是单变量决策，也就是判断条件只有一个（A）。实际上还有多变量决策树，也就是判断条件是多个（A&B），不再选择一个特征，而是一组特征。相应的决策树会更复杂，开销越更大，比如OC1算法，这里不多介绍。

（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

处理连续值

---

打网球数据集中全是离散值，那对于连续值又该如何处理？

比如下表数据集，A和B是两个连续值特征，Y是标签。

A	B	Y
1	2	yes
3	6	no
4.6	8	no
6	4	yes

假定特征$a$在数据集$D$上有$n$个不同取值，排序后记为 { a 1 , a 2 , . . . , a n } \{a^1,a^2,...,a^n\} {a1,a2,...,an}，将每相邻2个取值的均值作为一个分割点$T$：
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } T_a=\{\frac{a^i+a^{i+1}}{2}|1\leq i\leq n-1\} Ta​={2ai+ai+1​∣1≤i≤n−1}

比如对于特征值A来说，排序后得到{1，3，4.6，6}，分割点 T A = { 1 + 3 2 , 3 + 4.6 2 , 4.6 + 6 2 } = { 2 , 3.8 , 5.4 } T_A=\{\frac{1+3}{2},\frac{3+4.6}{2},\frac{4.6+6}{2}\}=\{2,3.8,5.4\} TA​={21+3​,23+4.6​,24.6+6​}={2,3.8,5.4}。

比如对于特征值B来说，排序后得到{2，4，6，8}，分割点 T A = { 2 + 4 2 , 4 + 6 2 , 6 + 8 2 } = { 3 , 5 , 7 } T_A=\{\frac{2+4}{2},\frac{4+6}{2},\frac{6+8}{2}\}=\{3,5,7\} TA​={22+4​,24+6​,26+8​}={3,5,7}。
也就是将连续值离散化，得到上述3个离散值，根据是否小于该值来划分，只有C4.5算法和CART算法可以使用连续值，再选择基尼指数最小的分割点来分割该特征，然后再选择基尼指数小的特征作为划分依据。

比如对应分割点$T_A=2$，特征A分为2个子集 { { 1 } , { 3 , 4.6 , 6 } } \{\{1\},\{3,4.6,6\}\} {{1},{3,4.6,6}}，记为$U_1$和$U_2$，计算基尼指数：
$Gini(D,U_1)=1-({\frac{1}{1}}^2+{\frac{0}{1}}^2)=0$
$Gini(D,U_2)=1-({\frac{1}{3}}^2+{\frac{2}{3}}^2)=0.44$
$Gini\_index(D,T_A=2)=\frac{1}{4}\times 0+\frac{3}{4}\times 0.44=0.33$
类似的，计算其他分割点：
$Gini\_index(D,T_A=3.8)=\frac{2}{4}\times 0.5+\frac{2}{4}\times 0.5=0.5$
$Gini\_index(D,T_A=5.4)=\frac{3}{4}\times 0.44+\frac{1}{4}\times 0=0.33$
故说特征A可以选分割点2或5.4，$Gini\_index(D,A)=Gini\_index(D,T_A=2)=0.33$。

对于特征B：
$Gini\_index(D,T_B=3)=\frac{1}{4}\times 0+\frac{3}{4}\times 0.44=0.33$
$Gini\_index(D,T_B=5)=\frac{2}{4}\times 0+\frac{2}{4}\times 0=0$
$Gini\_index(D,T_B=7)=\frac{3}{4}\times 0.44+\frac{1}{4}\times 0=0.33$
故特征B应选分割点5，$Gini\_index(D,B)=Gini\_index(D,T_B=5)=0$。

然后决策选择特征A还是特征B作为划分依据：
$Gini\_index(D,A)>Gini\_index(D,B)$
故选择特征B作为划分依据。

剪枝

---

剪枝主要是为了解决过拟合的问题，包括预剪枝和后剪枝两种。

• 预剪枝

预剪枝是在划分决策树之前进行剪枝，列举几种方法。

（1）指定结点所包含的最⼩样本数⽬。当结点总样本数⼩于该值时则不再分。
（2）指定树的深度。当树的最⼤深度大于该值时则往下不再划分。
（3）指定叶子节点个数。当叶子节点树大于该值则不再划分。
（4）指定叶子节点所含最小样本数。当叶子节点所含样本小于该值时，则会和兄弟叶子节点一起被剪枝。

往往使用预剪枝更多。

• 后剪枝

后剪枝是在已⽣成的决策树上进⾏剪枝。

得到决策树后，便可以验证精度，然后依次将某些中间结点剪枝掉，再计算精度，若精度提高了则剪枝该结点，反之不剪枝。

应用示例

---

使用sklearn中封装的DecisionTreeClassifier()函数构建决策树，包括主要参数：

• criterion
  划分依据，可取gini（默认）或"entropy"，即CART算法或ID3算法。
• min_samples_split
  结点所包含的最⼩样本数⽬，默认2，即预剪枝方法（1）。
• max_depth
  决策树最⼤深度，即预剪枝方法（2）。
• max_leaf_nodes
  最大叶子节点数，即预剪枝方法（3）。
• min_samples_leaf
  叶⼦节点最少样本数，默认1，即预剪枝方法（4）。
• random_state
  随机数种⼦。

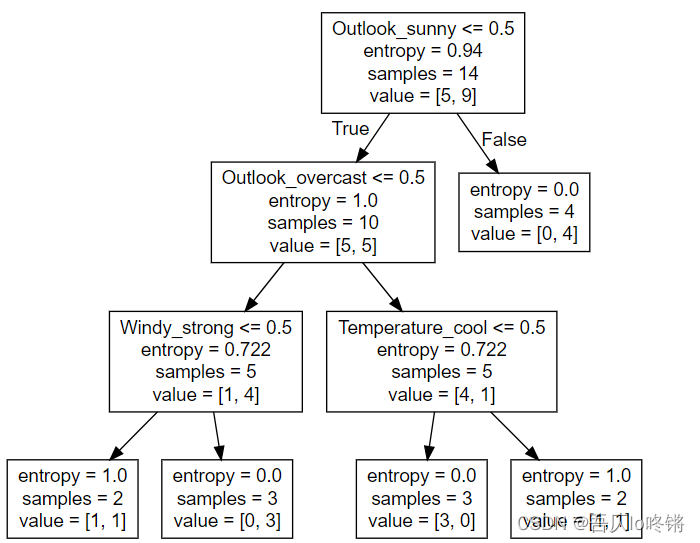
例1. ID3算法
在Kaggle中下载打网球数据集，最后使用在线Graphviz可视化决策树。

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz

# 读数据
data = pd.read_csv('D:\\play_tennis.csv')
x = data[['outlook', 'temp', 'humidity', 'wind']]
y = data['play']
# 数据处理
transfer = DictVectorizer(sparse=False)
x = transfer.fit_transform(x.to_dict(orient="records"))  # 转为onehot
# 创建模型
estimator = DecisionTreeClassifier(criterion="entropy",max_depth=3)  # 使用ID3,最大深度3
estimator.fit(x, y)  # 训练
# 数据太少了，就没有测试和评估
# 可视化，保存为.dot文件
export_graphviz(estimator, out_file="D:\\tennis.dot",
                feature_names=['Outlook_overcast', 'Outlook_rain', 'Outlook_sunny', 'Temperature_cool',
                               'Temperature_hot', 'Temperature_mild', 'Humidity_high', 'Humidity_normal', 'Windy_waek',
                               'Windy_strong'])

例2. CART算法-分类
使用自带鸢尾花数据集，4特征3分类。

from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz

iris = load_iris()  # 读数据集
x = iris.data
y = iris.target
# 划分训练集测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=20221020)
# 创建模型
estimator = DecisionTreeClassifier(max_depth=4, min_samples_split=3)  # 最大深度4，最小样本数3
estimator.fit(x_train, y_train)  # 训练
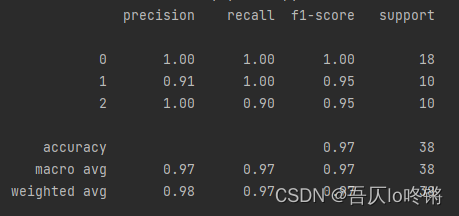
y_pred = estimator.predict(x_test)  # 测试
print(classification_report(y_test, y_pred))  # 评估
# 可视化
export_graphviz(estimator, out_file="D:\\iris.dot",
                feature_names=["sepal length", "sepal width", "petal length", "petal width"])

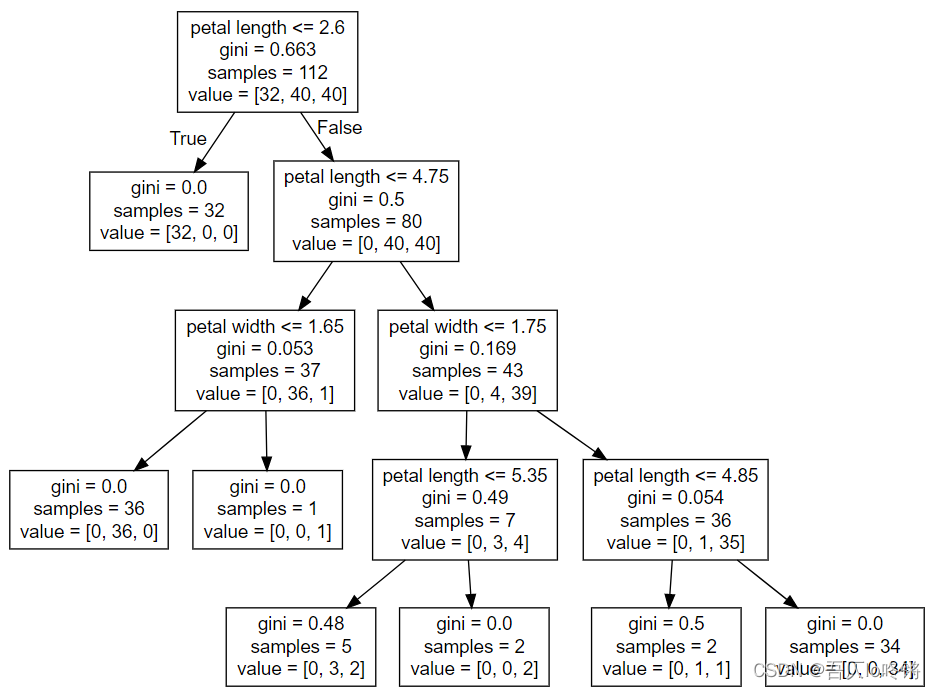
例3. CART算法-回归

import numpy as np
from matplotlib import pyplot as plt
from sklearn.tree import DecisionTreeRegressor,export_graphviz

np.random.seed(20221021)
X = np.linspace(0, 5, 100)  # 生成数据
y = X ** 2 + 5 + np.random.randn(100)
x = X.reshape(-1, 1)
# 创建模型
estimator = DecisionTreeRegressor(max_depth=5, max_leaf_nodes=10)  # 最大深度5，最多叶子10
estimator.fit(x, y)  # 训练
y_pred = estimator.predict(x)  # 测试
# 可视化
export_graphviz(estimator, out_file="D:\\乌七八糟\\refression.dot", feature_names=["x"])
plt.scatter(X, y, color='lightblue')
plt.plot(x, y_pred, color='red')
plt.show()

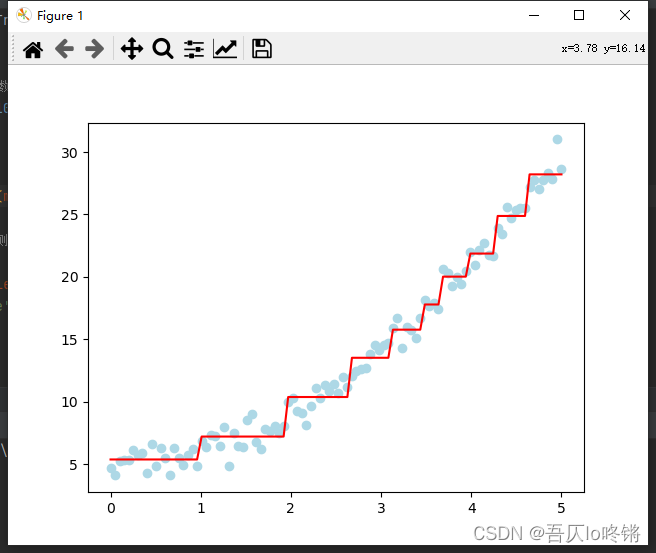
回归效果其实并不好，不是过拟合就是阶梯状。

原创不易，请勿转载（本不富裕的访问量雪上加霜 ）
博主首页：https://wzlodq.blog.csdn.net/
来都来了，不评论两句吗👀
如果文章对你有帮助，记得一键三连❤