同济高等数学第二章之经典错误知识点笔记

1.导数

1.概念

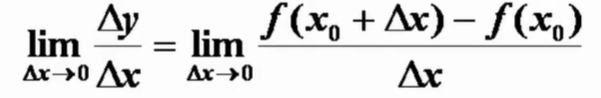
可导是左右导数都存在且相等充分必要条件。

2.微分

定理一：

定理二:
y=f(x)在点x0处可微的充分必要条件是f(x)在点x0处可导。

3.导数与微分的几何意义

切线方程：

法线方程：
法线：法线指平面上垂直于曲线在某点的切线的一条线。

法线*切线=-1

微分：

4.可微，可导，连续之间的关系

连续不一定可微，或可导。例如：|x|。

f(x)可导不能推出f'(x)连续，也不能推出f'(x)的极限存在。
例如：

5.基本初等函数导数格式

6.求导法则

1.有理运算法则

2.复合函数求导法

3.隐函数求导法

4.反函数的导数

前提f(x)处处可导，且f'(x)≠0。

5.参数方程求导

7.高阶导数

注：如果函数f(x)在点x处n阶可导，则在点x的某领域内f(x)必定具有一切低于n阶的导数。

常用的高阶导数公式：