如何简单地理解时间序列分析_时间序列反射率变化代表什么意思-CSDN博客

什么是时间序列？

时间序列也称动态序列，是指将某种现象的指标数值按照时间顺序排列而成的数值序列。大量的社会经济统计指标都是依据年、季度、月、日，甚至实时（秒）统计的，因此，时间序列是某个统计指标（变量）长期变动的数值表现。
时间序列由两个组成要素构成：1、第一个要素是时间要素；2、第二个要素是数值要素。时间序列根据时间和数值性质的不同，可以分为时期时间序列和时点时间序列。例如下方某间食杂店的销售额时间序列，就是时期时间序列，统计的是每一年，在一年时间内该食杂店的销售总额。

又如下方某家制造工厂的动能部门，表格数据表示锅炉的分时温度数据。每隔一个小时，系统自动记录一次锅炉的实时温度。可以发现，这里的温度数据是某个时间点的实时数据，所以该时间序列为时点时间序列。

时间序列可以反映某个现象的发展变化状态。通过对时间序列的分析，可以反映现象发展变化的趋势和规律，再通过对影响时间序列的各种因素进行测定，可以进一步解释现象变化的内在原因，为预测和决策提供可靠的数据支持。

时间序列分解

因为时间序列是某个指标数值长期变化的数值表现，所以时间序列数值变化背后必然蕴含着数值变换的规律性，这些规律性就是时间序列分析的切入点。一般情况下，时间序列的数值变化规律有以下四种：长期变动趋势、季节变动规律、周期变动规律和不规则变动。不同的数值变化规律是由不同影响因素决定的。这些影响因素有长期起作用的因素，也有短期因素；有可以预知和控制的因素，也有未知和不可控制的因素；这些因素相互作用和影响，从而使时间序列的变化趋势呈现不同的特点。根据影响因素对时间序列数值变化趋势的不同影响情况，可以分为四种影响因素：长期趋势影响因素、季节变动影响因素、循环变动影响因素和不规则变动影响因素。

长期趋势

长期趋势指的是统计指标在相当长的一段时间内，受到长期趋势影响因素的影响，表现出持续上升或持续下降的趋势，通常用字母 T 表示。例如，随着国家经济的发展，人均收入将逐渐提升；随着科学技术的发生，劳动生产率也不断提高。

季节变动

季节变动是指由于季节的转变使得指标数值发生周期性变动。由此可见，指标数值的季节变动是以年为周期的，一般以月、季、周为时间单位，不能以年作单位，通常用 S 表示。引起季节变动的因素有自然因素，也有人为因素。例如，蔬菜食品价格，棉衣销售量都会随着季节气温的变化而周期变化；每年的长假（五一、十一、春节）都会引起出行人数的大量增加。

循环变动

循环变动与季节变动的周期不同，循环变动通常以若干年为周期，在曲线图上表现为波浪式的周期变动。这种周期变动的特征变现为增加和减少交替出现。最典型的周期案例就是市场经济的商业周期。

不规则变动

不规则变动是由某些随机因素导致的数值变化，这些因素的作用是不可预知和没有规律性的，因此对数值的变化影响变形为不规则变动。

以上四种变动就是时间序列数值变化的分解结果。有时这些变动会同时出现在一个时间序列里面，有时也可能只出现一种或几种，这是由引起各种变动的影响因素决定的。正是由于变动组合的不确定性，时间序列的数值变化才那么千变万化。四种变动与指标数值最终变动的关系可能是叠加关系，也可能是乘积关系。
叠加模型：如果四种变动之间是相互独立的关系，那么叠加模型可以表示为：

乘积模型：如果四种变动之间存在相互影响关系，那么应该使用乘积模型：

反映在具体的时间序列图上，如果随着时间的推移，序列的季节波动变得越来越大，则反映各种变动之间的关系发生变化，建议使用乘积模型；反之，如果时间序列图的波动保持恒定，则可以直接使用叠加模型。

时间序列分析

时间序列分析分成两种形式：第一种是传统的时间序列分析方法，研究时间序列是否能被分解成上面介绍的四种变动，并解析引起每种变动的影响因素。第二种是时间序列的模型解析法，常用时间序列模型有自回归（AR）模型、滑动平均（MA）模型、自回归滑动平均（ARMA）模型等。

时间序列分解成四种数值变动类型，草堂君在很早之前的文章中已经详细介绍过，大家可以点击下方文章链接回顾：1、长期趋势分析：长期趋势分析；2、季节变动分析：季节变动分析；3、循环变动及不规则变动分析：循环变动和不规则变动；

后面的文章将重点介绍几种常用的时间序列模型：指数平滑模型、自回归（AR）模型、滑动平均（MA）模型、自回归滑动平均（ARMA）模型。文章将介绍这些模型的分析原理以及如何使用 SPSS 进行这些模型的时间序列分析。

因为传统时间序列分析技术（时间序列分解法）的缺陷，所以统计学家开发出更为通用的时间序列分析方法，其中 AR/MA/ARMA/ARIMA 在这个发展过程中扮演了非常重要的角色，直到现在，它们都在实际工作生活中发挥重要作用。这四种分析方法的共同特点都是跳出变动成分的分析角度，从时间序列本身出发，力求得出前期数据与后期数据的量化关系，从而建立前期数据为自变量，后期数据为因变量的模型，达到预测的目的。来个通俗的比喻，大前天的你、前天的你、昨天的你造就了今天的你。

虽然 AR/MA/ARMA/ARIMA 是四种可以独立使用的分析方法，但是它们其实是互补的关系，适用于包含不同变动成分的时间序列。由于这四种分析方法涉及的原理解释起来需要大量篇幅，所以草堂君在这里做通俗介绍。
时间序列的平稳性
通俗介绍四种时间序列分析法之前，需要先回顾前面介绍的一个知识点，平稳时间序列和非平稳时间序列，AR/MA/ARMA 用于分析平稳时间序列，ARIMA 通过差分可以用于处理非平稳时间序列。平稳时间序列和非平稳时间序列如下面两幅图所示：

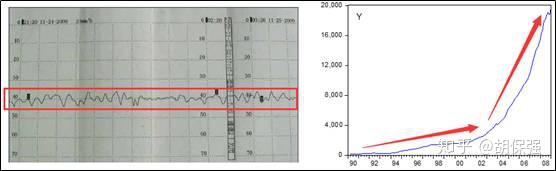
左边的图是工业生产中的温度时间序列，它是围绕一个常数上下波动的，也就是计算时间序列所有数值的平均值，会等于这个常数。工业生产中对液面、压力、温度的控制过程；某地的气温变化过程；某条河流的水位变化过程基本都属于平稳时间序列。
右边的图是中国外汇储备额的时间序列，可以发现这个时间序列是有持续增长的，先慢后快，这是一个非平稳时间序列。在经济领域，例如一个国家的 GDP、进出口额的时间序列基本都是非平稳时间序列。

一般具有长期趋势的时间序列都是非平稳时间序列。根据趋势的不同，可以使用差分将具有长期趋势的时间序列转换成平稳时间序列。例如，线性增长的长期趋势，可以通过一阶差分形成新的平稳的（消除长期趋势）时间序列：

例如，时间序列的数值为线性增长的 (1,2,3,4,5,6,7,8)，经过一阶差分以后，新的时间序列的数值为 (1,1,1,1,1,1,1)，就成为稳定的时间序列了。
根据长期趋势的发展趋势不同，可以进行差分的次数和方法也不相同，一般的规律如下：

一次差分的时间序列数值大体相同，配合直线趋势；
二次差分的时间序列数值大体相同，配合二次曲线
对数的一次差分的时间序列数值大体相同，配合指数曲线
一次差分的环比值大体相同，配合修正指数曲线
对数一次差分的环比值大体相同，配合 Gompertz 曲线
倒数一次差分的环比值大体相同，配合 Logistic 曲线

AR/MA/ARMA 模型

这四种模型的名称都是它们英文全称的缩写。AR 模型称为自回归模型（Auto Regressive model）；MA 模型称为移动平均模型（Moving Average model）；ARMA 称为自回归移动平均模型（Auto Regressive and Moving Average model）；ARIMA 模型称为差分自回归移动平均模型。

AR 模型

如果某个时间序列的任意数值可以表示成下面的回归方程，那么该时间序列服从 p 阶的自回归过程，可以表示为 AR§：

可以发现，AR 模型利用前期数值与后期数值的相关关系（自相关），建立包含前期数值和后期数值的回归方程，达到预测的目的，因此成为自回归过程。这里需要解释白噪声，大家可以将白噪声理解成时间序列数值的随机波动，这些随机波动的总和会等于 0，例如前面统计基础文章中介绍的，某条饼干的自动化生产线，要求每包饼干为 500 克，但是生产出来的饼干产品由于随机因素的影响，不可能精确的等于 500 克，而是会在 500 克上下波动，这些波动的总和将会等于互相抵消等于 0。

MA 模型

如果某个时间序列的任意数值可以表示成下面的回归方程，那么该时间序列服从 q 阶的移动平均过程，可以表示为 MA(q)：

可以发现，某个时间点的指标数值等于白噪声序列的加权和，如果回归方程中，白噪声只有两项，那么该移动平均过程为 2 阶移动平均过程 MA(2)。比较自回归过程和移动平均过程可知，移动平均过程其实可以作为自回归过程的补充，解决自回归方差中白噪声的求解问题，两者的组合就成为自回归移动平均过程，称为 ARMA 模型。

ARMA 模型

自回归移动平均模型由两部分组成：自回归部分和移动平均部分，因此包含两个阶数，可以表示为 ARMA(p,q)，p 是自回归阶数，q 为移动平均阶数，回归方程表示为：

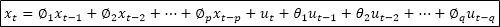
从回归方程可知，自回归移动平均模型综合了 AR 和 MA 两个模型的优势，在 ARMA 模型中，自回归过程负责量化当前数据与前期数据之间的关系，移动平均过程负责解决随机变动项的求解问题，因此，该模型更为有效和常用。

ARIMA 模型

介绍时间序列平稳性时提到过，AR/MA/ARMA 模型适用于平稳时间序列的分析，当时间序列存在上升或下降趋势时，这些模型的分析效果就大打折扣了，这时差分自回归移动平均模型也就应运而生。ARIMA 模型能够用于齐次非平稳时间序列的分析，这里的齐次指的是原本不平稳的时间序列经过 d 次差分后成为平稳时间序列。

在现实生活中，存在很多非平稳的时间序列，它们的均值和方差是随着时间的变化而变化的，幸运的是，统计学家们发现，很多时间序列本身虽然不平稳，但是经过差分（相邻时间点的指标数值相减）之后，形成的新时间序列就变成平稳时间序列了。因此，差分自回归移动平均模型写成 ARIMA(p,d,q)。p 代表自回归阶数；d 代表差分次数；q 代表移动平均阶数。在 spss 软件中，有时输出的 ARIMA 模型包括 6 个参数：ARIMA(p,d,q)(P,D,Q)，这是因为如果时间序列中包含季节变动成分的话，需要首先将季节变动分解出来，然后再分别分析移除季节变动后的时间序列和季节变动本身。这里小写的 p,d,q 描述的是移除季节变动成分后的时间序列；大写的 P,D,Q 描述的是季节变动成分。两个部分是相乘的关系。因此，ARIMA(p,d,q)(P,D,Q) 也被称为复合季节模型。

总结一下

时间序列分析的文章更新到这里，总共介绍了两个时间序列分析的体系：时间序列分解模型体系和 AR/MA/ARMA/ARIMA 模型体系。两者的分析原理是不同的，时间序列分解是力求将时间序列分解成不同的变动成分，分析每种变动成分的规律，然后在综合各种成分的规律用于预测；AR/MA/ARMA/ARIMA 模型体系是从时间序列数值本身的相关关系出发，将移动平均技术、相关分析技术和平稳技术（差分）等纳入模型，力求建立时间序列数值之间的回归方程，从而达到预测的目的。