计算机组成原理——现代计算机的数制、编码和计算

数制

进位计数法

在进位计数法中（以十进制为例），每个数位所用到的数码（0-9）的个数称为基数（10），每个数位记满基数后就向高位进位。

每个数码所表示的数值等于该数码本身乘以一个与它所在数位有关的常数，这个常数称为位权

一个进位数的数值大小就是它的各位数码按权相加：
$$9527=9\times 10^3+5\times 10^2+2\times 10^1+7\times 10^0$$

在计算机系统内部，所有信息都使用二进制进行编码，这样做的原因如下：

• 二进制只有两种状态，使用具有两个稳定状态的物理器件就可以表示二进制数的每一位。
• 二进制的两种状态正好与逻辑值的真和假对应。
• 二进制的编码和运算规则比较简单，使用逻辑门电路就可以实现。

$$9527_{10}=10010100110111_2$$

通常会使用八进制和十六进制方便的表示二进制数：
$$9527_{10}=10010100110111_2=22467_8=2537_{16}$$

不同进制数之间的相互转换

二进制数转换为八进制数和十六进制数

对于一个二进制混合数（既包含整数部分又包含小数部分），在转换时应以小数点为界，整数部分，从小数点开始往左数，将一串二进制分为3位（八进制）一组或四位（十六进制）一组，在数的最左边可根据需要加0补齐；小数部分，从小数点开始往右数，也将一串二进制分为3位（八进制）一组或四位（十六进制）一组，在数的最右边可根据需要加0补齐，最终使总的位数为3或4的整数倍，然后分别用对应的八进制数或十六进制数取代。
$$\begin{gathered} 10010100110111_2 \\ \Downarrow \\ 0010010100110111 \\ \Downarrow \\ 2537_{16} \end{gathered}$$

任意进制数转换为十进制数

将任意进制数的各位数码和它们的权值相乘，再把乘积相加，就得到了一个十进制数，这种方法称为按权展开相加法。
$$\begin{gathered} 2537_{16} \\ \Downarrow \\ 2\times 16^3+5\times 16^2\times 3\times 16^1+7\times 16^0 \\ \Downarrow \\ 9527_{10} \end{gathered}$$

十进制数转换为任意进制数

对十进制数的整数部分采用除基取余法：整数部分除基取余，最先取得的余数为数的最低位，最后取得的余数为数的最高位，商为0时结束；对十进制的小数部分采用乘基取整法，小数部分乘基取整，最先取得的整数为数的最高位，最后取得的整数为数的最低为，乘积为1（或满足精度，因为在计算机中，整数可以连续表示，而小数是离散的）时结束。

编码

真值和机器数

日常生活中，通常使用正负号表示正数和负数，这种带正负符号的数就称为真值。在计算机中，通常将数的符号和数值部分一起编码，将数值的符号数字化，用0表示正号，1表示负号。这种将符号数字化的数称为机器数，机器数所表示的实际值就是真值。在计算机中，根据小数点的位置是否固定将机器数分为定点数和浮点数，并且常使用原码、补码、反码和移码表示法来表示机器数。

机器数的定点表示法

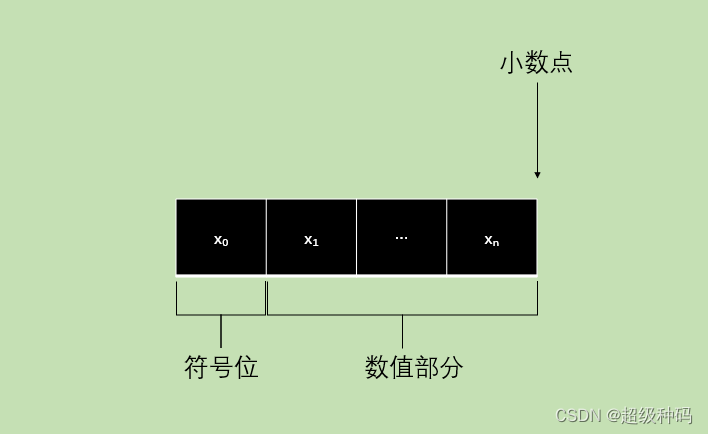
定点小数和定点整数

定点表示法用于表示定点小数和定线整数。

• 定点小数：定点小数是纯小数，约定约定小数点位置在符号位之后、有效数值部分最高位之前。

• 定点整数：定点整数是纯整数，约定小数点位置在有效数值部分最低位之后。

原码表示法

原码表示法：用机器数的最高位表示数的符号，其余各位表示数的绝对值。

• 纯小数的原码定义如下（注：下文在不说明的情况下均以字长为n+1示例）：
  $$[x{]}_{原}=\{\begin{array}{l}x,0\le x<1\\ 1+|x|,-1<x\le 0\end{array}(x为真值)$$
• 纯整数的原码定义如下：
  $$[x{]}_{原}=\{\begin{array}{l}x,0\le x\le 2^n-1\\ 2^n+|x|,-(2^n-1)\le x\le 0\end{array}$$

原码表示法的优点是与真值的相互转换简单；缺点是0的表示不唯一并且符号位不能参与运算。

补码表示法

在介绍补码之前，先了解几个概念和性质：

• 模：模是指一个计量系统的计数范围，本质上是计量系统产生溢出的值，这个值在计量系统中表示不出来，计量系统上只能表示出模的余数。并且，模是不分符号的，不存在有符合和无符号情况下之说。
• 取模：两个整数$a,b$，把计算$a-b\lfloor a÷b\rfloor$的过程称为模运算，记作$amodb$。
• 同余：两个整数$a,b$，若$amodm=bmodm$，则称$a$与$b$对于模$m$同余。记作$a\equiv b(modm)$。
• $a\equiv a(modm)$。
• 若$a\equiv b(modm)，c\equiv d(modm)$，那么 $$\begin{gathered} a+c\equiv b+d(modm) \\ a\times c\equiv b\times d(modm) \end{gathered}$$

在一个具有模的计量系统中，只需要找到负数的一个正数同余数，就可以将所有减法运算转换为加法运算。在计算机中，由于计算机的字长是固定的，所以可以将计算机看作一个模为$2^{n+1}$的计量系统。那么就可以使用同余数进行编码，这就编码方式就称为补码表示法。补码中符号位即代表了数的正确符号，又表示同余数中的一个数位，因此在补码运算中，符号位可以与数值位一起参加运算。纯小数的补码定义如下：

$$[x{]}_{补}=\{\begin{array}{l}x,0\le x＜1\\ 2+x,-1\le x\le 0\end{array}(mod2)$$

纯整数的补码定义如下：

$$[x{]}_{补}=\{\begin{array}{l}x,0\le x\le 2^n-1\\ 2^{n+1}+x,-2^n\le x\le 0\end{array}(mod{2}^{n+1})$$

相较于原码表示法，补码表示法0的表示唯一、加减运算统一采用加法操作实现并且负数的表示范围增加。

反码表示法

反码表示法：正数的反码还是等于原码；负数的反码就是它的原码除符号位外，按位取反。通常使用来由原码求补码或者由补码求原码的过渡码。

• 纯小数的反码定义如下：
  $$[x{]}_{反}=\{\begin{array}{l}x,0\le x<1\\ 2-2^n,-1<x\le 0(mod2-2^n)\end{array}$$
• 纯整数的反码定义如下：
  $$[x{]}_{反}=\{\begin{array}{l}x,0\le x\le 2^n-1\\ 2^{n+1}-1+x,-(2^n-1)\le x\le 0\end{array}$$

移码表示法

移码表示法：在真值上加上一个常数（偏置值），通常这个常数为$2^n$，相当于$x$在数轴上向正方向移动了若干个单位。通常使用移码表示浮点数的阶码，它只能表示整数。
$$[x{]}_{移}=2^n+x,-(2^n-1)\le x\le 2^n-1$$

原码、反码、补码和移码的相互转换

机器数的浮点表示法

浮点数表示法类似于十进制的科学计数法，它以适当的形式将比例因子表示在数据中，让小数点的位置根据需要而浮动。这样，在数位有限的情况下，既扩大了数的表示范围，又保持了数的有效精度。

格式和范围

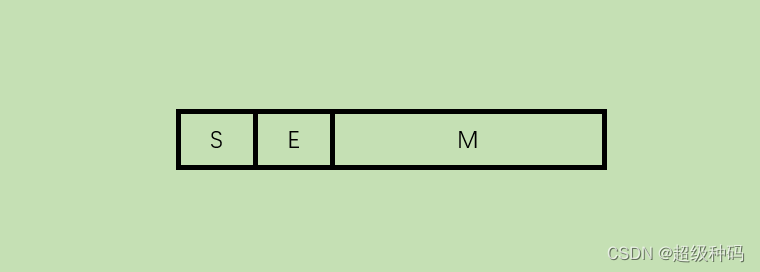
浮点数的格式表示为：
$$N=(-1{)}^S\times M\times R^E$$

其中：

• S取值0或1，用来表示浮点数的符号。
• M是一个二进制定点小数，称为尾数，一般用定点原码小数表示。M的位数反应浮点数的精度。
• E是一个二进制定点整数，称为阶码或指数，用移码表示。E的值反应浮点数的小数点的位置，阶码的位数反应浮点数的表示范围。
• R是基数，可以约数为2、4、16等。

浮点数的范围是关于原点对称的：

上溢：

• 运算结果大于最大正数时称为正上溢。
• 运算结果小于最小负数时称为负上溢。

下溢：

• 运算结果在0和最小正数之间称为正下溢。
• 运算结果在最大负数和0之间称为负下溢。

数据产生上溢，计算机必须中断运算操作，进行溢出处理；数据产生下溢，浮点数值趋于0，计算机将其当作机器数0处理。

浮点数的规格化

尾数的位数决定浮点数的有效数位，有效数位越多，数据的精度越高。为了在浮点数运算过程中尽可能的保留有效数字的位数，使有效数字尽量占满尾数位数，必须在运算过程中对浮点数进行规格化操作。所谓规格化操作，是指通过调整一个非规格化浮点数的尾数和阶码的大小，使非零的浮点数在尾数的最高数位上保证是一个有效值。

• 左规：当运算结果的尾数的最高位置不是有效位，即出现$\pm \mathrm{0.0...0}\times ...\times$的形式时，需要进行左规。左规时，尾数每左移一位、阶码减一（基数为二），直至尾数变成规格化形式为止，左规可能要进行多次。
• 右规：当运算结果的尾数的有效位进到小数点前面时，需要进行右规。将小数点右移一位、阶码加1（基数为2时）。需要右规时，只需要及逆行一次。

IEEE754

IEEE754是一种浮点数的规范，IEEE754规定常用的浮点数格式有短浮点数、长浮点数和临时浮点数：

类型	数符	阶码	尾数数值	总位数	偏置值	最小值	最大值
短浮点数	1	8	23	32	7FH	$2^{-126}$	$2^{127}\times (2-2^{-23})$
长浮点数	1	11	52	64	3FFH	$2^{-1022}$	$2^{1023}\times (2-2^{-52})$
临时浮点数	1	15	64	80	3FFFH

其中短浮点数和长浮点数尾数采用隐藏位策略的原码表示，阶码用移码表示。其中隐藏位策略是指默认尾数的最高位总是一，这就可以不记录这个值从而让尾数多表示一位有效位。IEEE754标准的浮点数，阶码全0或全1时有特定的含义：

值的类型	单精度				双精度
	符号	阶码	尾数	值	符号	阶码	尾数	值
正零	0	0	0	0	0	0	0	0
负零	1	0	0	-0	1	0	0	-0
正无穷大	0	255	0	∞	0	2047	0	∞
负无穷大	1	255	0	-∞	1	2047	0	-∞

定点数和浮点数的区别

现代计算机的编码

现代计算机使用不同的编码表示不同性质的数：

• 整数的表示：
  • 无符号整数：无符号整数的默认符号为正，因此可以看作采用省略符号位的原码表示法表示。
  • 有符号整数：反码表示法表示。
• 小数的表示：浮点表示法。

数据的存储和排列

现代计算机基本上采用字节编址，即每个地址编号对应1字节内存，不同类型的数据占用的字节数不同，而程序中每个数据只给定一个地址，那这个地址是是哪个地址呢？

大小端模式

多字节数据存放在连续的内存中，用最高有效字节（LSB）和最低有效字节（MSB）来表示数据的低位和高位。根据数据字节在内存中存放的顺序不同，可以采取以下两种存储方式：

• 大端模式：按最高有效字节到最低有效字节的顺序存储。
• 小端模式：按最低有效字节到最高有效字节的顺序存储。

边界对齐

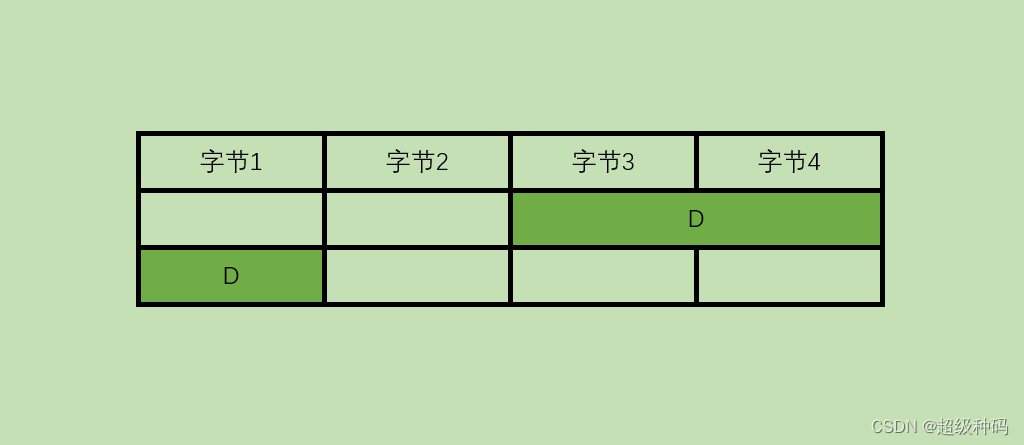
边界对齐是指当存储的数据长度不够半字或字长度时，通过添加空白字节使其满足长度的存储方式。而非边界对齐是指充分利用每一个字节，不留空白的存储方式。假设现有一台32位可按字节、半字和字寻址的计算机，一个长度为3B的数据D，如果数据以边界对齐的方式存放，那么这个数据可以通过一次字寻址就全部取出。

但如果使用非边界对齐的方式存放，恰巧这个数据有1B存储到了第一个字，有2B存储到了第二个字，那么无论采用哪种寻址方式都不能通过一次寻址就把这个数据全部取出。此时需要进行两次寻址，并且对高低字节的位置进行调整、连接之后才能得到想要的数据，从而影响了指令的执行效率。