计算机组成原理——第二章数据的表示和运算（上）

提示：日出有盼，落日有念，心有所期，忙而不茫

---

前言

这里主要是根据王道考研视频所作的第二章，这一章主要探讨两个问题，数据如何再计算机中表示?，运算器如何实现数据的算数，逻辑运算？

---

提示：以下是本篇文章正文内容，下面案例可供参考

2.1.1 进位计数制

在计算机系统内部，所有的信息都是用二进制进行编码的，这样做的原因有以下几点。
1）二进制只有两种状态，使用有两个稳定状态的物理器件就可以表示二进制数的每一位，
制造成本比较低，例如用高低电平或电荷的正负极性都可以很方便地表示0和1.
2）二进制位1和0正好与逻辑值“真”和“假”对应，为计算机实现逻辑运算和程序中的逻辑判断提供了便利条件。
3)二进制的编码和运算规则都很简单，通过逻辑门电路能方便地实现算术运算。
任意进制转化十进制
二进制转化为八进制
三个二进制数正好可以表示八种不同的状态
以小数点开始左右3位为一组，每组转化为对应的八进制符号（高位整数补零，地位小数补零，使得最终总的位数是3 的整数倍）

二进制转化为十六进制
四个二进制数正好可以表示十六种不同的状态
以小数点开始左右4位为一组，每组转化为对应的16进制符号

八进制转化二进制
同样，由八进制数或十六进制数转换成二进制数，只需将每位改为3位或4位二进制数即可（必要时去掉整数最高位或小数最低位的0)。八进制数和十六进制数之间的转换也能方便地实现，十六进数制转换为八进制数（或八进制数转换为十六进制数）时，先将十六进制（八进制）数转换为二进制数，然后由二进制数转换为八进制（十六进制）数较为方便。

注意这里的转化规则，比如小数101表示0.5

十六进制转化为二进制

进制的常见书写方式
二进制以B结尾，八进制以O开头，十六进制以H结尾或者以0x开头，十进制以D结尾

十进制转化为任意进制
注意:在计算机中，小数和整数不一样，整数可以连续表示,但小数是离散的;所以并不是每个十进制小数都可以准确地用二进制表示，例0.3,无论经过多少次乘二取整转换都无法得到精确的结果。但任意一个二进制小数都可以用十进制表示。

方法一
(除基取余法整数部分)：任意一个整数都可以写成整数X(R的一次方，二次方，一直到n-1次方，所以是可以整除的)部分加上余数K0(0~R)部分 ，所以我们除以R之后得到余数K0便是R的零次方上的数值,再用得到的商再除以R得到的便是K1（先取得的余是整数的低位）

（乘基取整法小数部分）：核心思想也是一样想办法把K-1算出来，这里发现乘上一个R便可直观的得到K-1的值 ，得到的结果再乘R得到的便是K-2的值（先取得的整是小数的高位）

方法二（拼凑法）
若是给你的十进制数不是特别大的话，可能使用这些拼拼凑凑的方法可能要快一些，假如要将十进制转化成八进制，完全可以先转化成二进制，然后二进制再三位一组转化为八进制
小结回顾
真值：符合人类习惯的数字
机器数：数字实际存到机器里的形式，正负号需要被“数字化”

2.1.2 BCD码（大纲已删）

BCD:用二进制编码的十进制
8421码
通过上述我们知道要想表示0~9这十个数，必须最少需要4bit,而4bit则可以表示16个值 ，这样也就会有6个冗余，8421码的提出便是为了快速转换，
8421码的相加：若是两个数对应的8421码相加的结果不在映射表中，也就是落到了10~15这个区间这个时候我们再加上6 这样就一定会向高位进一个1，而低位所留下的部分又正好是我们个位所留下的部分

余3码
这是一种无权码，也就是在8421码的基础上加上一个0011得到不同的映射关系，因每个数都多余“3"，
2421码
是一种有权码，我们依然是使用四个二进制位来表示一个十进制位，不过这四个的权值是2421，同样需要注意0 ~ 4第一位都是零，5 ~ 9第一位则一定是1 这也是为了避免同一个值有不同的2421码（如5 0101或1011）

回顾

定点数：小数点的位置固定，浮点数：小数点的位置不固定。

这一小节我们先来看一下定点数的表示

2.1.3 无符号整数的表示和运算

这里主要探讨两个问题，无符号整数，在计算机硬件内，如何表示，无符号整数的加法，减法运算时怎么用硬件实现的
机器字长限定了每一次只能进行几个bit运算，机器字长也限制了通用寄存器只能有多少位（那个x寄存器就是一个通用寄存器，用来存放操作数）
无符号整数
全部二进制位都是数值位，没有符号位，第i位的位权是 2的i-1次方，nbit无符号整数表示的范围0~2的n次方-1 超出则溢出，意味着计算机无法一次处理这么多，可以表示的最小的数全是0，可以表示的最大的数全是1，一般在全部是正数运算且不出现负值结果的场合下，使用无符号整数表示。例如，可用无符号整数进行地址运算，或用它来表示指针。并且通常只有无符号整数而没有无符号小数。
无符号整数的减法运算
被减数不变，减数全部按位取反，末位+1减法变加法，从最低位开始，按位相加，并往最高位进位

知识点回顾

2.1.4 带符号整数的表示和运算(原反补)

首先我们这节主要解决的是带符号整数，在计算机硬件内，如何表示，第二，带符号整数的加法，减法运算是如何用硬件实现的？
同一个带符号整数可以用不同的编码方式表示 ，这便是原码 补码 反码，形式不同但是含义相同，将符号数值化，并将符号位放在有效数字的前面，就组成了带符号整数。虽然原码、补码、反码和移码都可以用来表示带符号整数，但补码表示有其明显的优势:
1）与原码和反码相比，0的补码表示唯一。
2）与原码和移码相比，补码运算规则比较简单，且符号位可以和数值位一起参加运算。
3）与原码和反码相比，补码比原码和反码多表示一个最小负数。
原码表示法
分为符号位和数值位 符号位0正1负 其实也就是之前的表示方式，不过是使用一位来表示正负，其他的依然如之前的表示，这种把符号“数字化”的数称为机器数。常用的有原码、补码和反码表示法。如0,101(这里的逗号“,”仅为区分符号位与数值位）表示+5。注意这里假设的机器字长是n+1，若是未指明机器字长【X】原=1，0010011也可以写成1，10011也就是将符号位之后的两个0去掉。

原码的缺点：符号位不能参与运算，需要设计复杂的硬件电路才能处理，所以聪明的科学家也就想到了用补码来表示真值——符号位可以参与运算（正数的补码可以解释为位权，负数的补码不能解释为位权）
方法 一
正数的原码，反码，补码都是不变的
负数的原码到反码是符号位不变，数值位取反便可得到反码，反码末位+1得到补码
若是让你根据补码来求反码，你可以先求原码再求反码（或者也可以使用除符号位之外全部取反，然后末尾加一，这里使用的方式是第二种，从右往左找到第一个1 这个1左边的所有数值位按位取反便可得到原码）

方法二
从右往左找到第一个1，这个1左边的所有“数值位”按位取反（按照之前我们计算机计算的方法，把所有的数值位按位取反，末位加一个一，若是反码最后一个是一，并且这个一前面也是一，就会导致不断的向前进位，直到前面那个是零才会停止，也就导致从右往左第一个1的右边的值与原码是一致的，所以这也就是为什么我们从右往左找到第一个1，这个1左边的所有数值按位取反便可得到补码）

方法一是计算机处理的方式，我们若是手算的话 推荐第二种
带符号整数加法运算
若是规定机器字长则若是发生进位则会丢弃，
从低位开始，按位相加（符号位参与运算），并往更高位 进位

带符号整数减法运算
A-B=A+(-B),也就是将减数取负值，所以也就有了全部位取反
方法一：首先是全部位按位取反，然后末位加一，与上面负数求补码有所不同（符号位不变，数值位取反）
方法二：与之前类似，从右往左找到第一个1，此1左边的全部取反（之前负数求补码是数值位取反，这里是全部），右边的不变便可得到原码或者补码

这也就能和之前的无符号的减法相联系，减数 全部取反，末位加1，相联系
知识点回顾

2.1.5原反补码的特性对比

注意加红的即可，如若是-64-64 结果保存在原码中则会溢出，若是保存于补码中则不会溢出。

按照之前我们所说的0的原码反码有两种方式表示，0000,0000。1000,0000，取反码就是0000,0000和1111,1111.然后我们取末位加也就是0000,0000,和10000,0000,由于规定了机器字长也就高位舍弃也就是0000,0000.对于特定的多出来的一个编码1000,000是表示-2的7次方，同样在定点小数中也是规定1.0000000 表示的是-1，
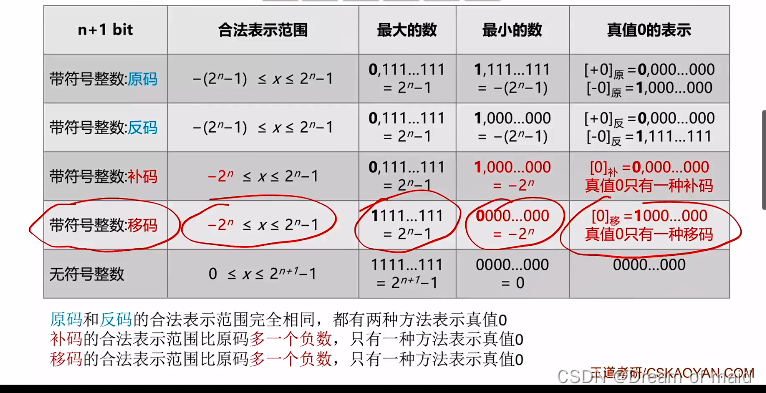
并且注意在确定位数的前提下，反码和补码，移码中最大值加一就是最小值的。

2.1.6 移码

若是偏置值是2的n次方，则移码相当于是补码的基础上将符号位取反，所以移码和补码是一一对应的，表示的范围自然也是一一对应
移码常用来表示浮点数的阶码。它只能表示整数。
移码就是在真值X上加上一个常数（偏置值)，通常这个常数取2的n次方，相当于X在数轴上向正方向偏移了若干单位，这就是“移码”一词的由来。
移码具有以下特点:
1)移码中零的表示唯一，[+0]移=2的n次方+0=[-0]移 =2"-0= 100…0(n个“0")。
2)一个真值的移码和补码仅差一个符号位
3)移码全0时，对应真值的最小值-2的n次方，移码全1时，对应真值的最大值2"-1。
4）移码保持了数据原有的大小顺序，移码大真值就大，移码小真值就小。
原码、补码、反码和移码这4种编码表示的总结如下:
1)原码、补码、反码的符号位相同，正数的机器码相同。
2)原码、反码的表示在数轴上对称，二者都存在+0和-0两个零。
3)补码、移码的表示在数轴上不对称，零的表示唯一，它们比原码、反码多表示一个数。
4)整数的补码、移码的符号位相反，数值位相同
5)负数的反码、补码末位相差1。
6)原码很容易判断大小。而负数的反码、补码很难直接判断大小，可采用如下规则快速判断:对于负数，数值部分越大，绝对值越小，真值越大（更靠近0)，正数自然是数值部分越大，绝对值越大，真值越大。

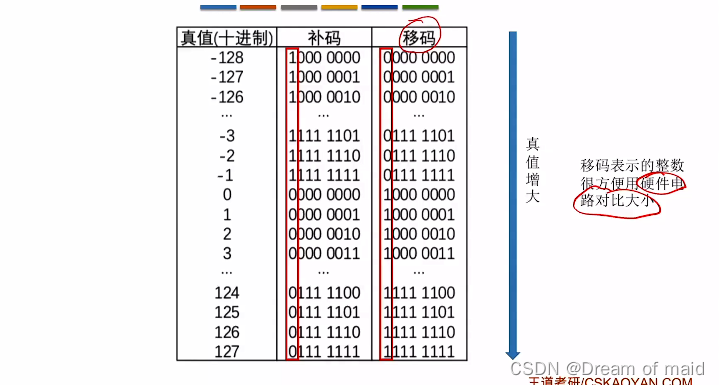
计算机可以很方便的从高位一次一次的进行对比，看哪一个先出现一也就是哪一个真值更大，

2.1.7 定点小数

我们固定小数点隐含在符号位的后面
反码，补码和上面是一样的 这里看一下区别
根据小数点的位置是否固定，在计算机中有两种数据格式:定点表示和浮点表示。在现代计算机中，通常用定点补码整数表示整数，用定点原码小数表示浮点数的尾数部分，用移码表示浮点数的阶码部分，历年统考真题的考点分布也基本落在这个范围内。若是说明了机器字长。注意这里是是要补齐八位的，小数是低位补0，整数是高位补0，
1)定点小数。定点小数是纯小数，约定小数点位置在符号位之后、有效数值部分最高位之前。若数据X的形式为X=x0x1x2x3x4。(其中x0为符号位，x1~x4是数值的有效部分，也称尾数，x1为最高有效位)，如下图左部分
2)定点整数。定点整数是纯整数，约定小数位置在有效数值部分最低位之后。若数据X的形式为X=x0x1x2x3x4(其中x0为符号位，x1~x4是尾数,x4为最低有效位)，如下图右边部分，也就是说定点小数计算真值时是从左往右加，定点整数是从右往左加。

另外一个需要注意的地方就是取值范围以及最小的数，还有真值零的表示

注意原码反码按照原点是对称的，而补码是不对称的，而补码多出来的一个都是最小值

拾遗

1） 没有特殊说明时 可默认BCD码就是8421码，若是所给的超过4位 补0便可，如这里（101001）BCD等于29D,而(101001)2等于29H
2） 2,1,5 的第12题还未领悟