图谱论学习—拉普拉斯矩阵背后的含义

一、为什么学习拉普拉斯矩阵

    早期，很多图神经网络的概念是基于图信号分析或图扩散的，而这些都需要与图谱论相关的知识。并且在图网络深度学习中（graph deep learning）中，拉普拉斯矩阵是很常用的概念，深入理解其物理含义非常有助于加深对GNN模型的理解。博主最近在学习GCN，想要在拉普拉斯矩阵方面有个更加深入的了解，看了不少文献资料与网上的解读，受益匪浅。

二、拉普拉斯矩阵的定义与性质

    对于一个有n个顶点的图G，它的拉普拉斯矩阵(Laplacian Matrix)定义为：$$L=D-A$$    其中，D是图G的度矩阵，A是图G的邻接矩阵。L中的元素可定义为：
$$L_{ij}=\{\begin{array}{ll}d(v_i)& 如果i=j\\ -A_{ij}& 如果i\ne j并且v_i与v_j之间有边\\ 0& 其他\end{array}$$    通常， 我们需要将拉普拉斯矩阵进行归一化。常用的有两种方式。
    (1) 对称归一化的拉普拉斯矩阵(Symmetric Normalized Laplacian Matrix)$$L^{sym}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$$    (2) 随机游走归一化的拉普拉斯矩阵(Random Walk Normalized Laplacian Matrix)$$L^{rw}=D^{-1}L=I-D^{-1}A$$    以下面这个图为例，假设每条边权重为1，得到这个图的邻接矩阵、度矩阵和拉普拉斯矩阵。

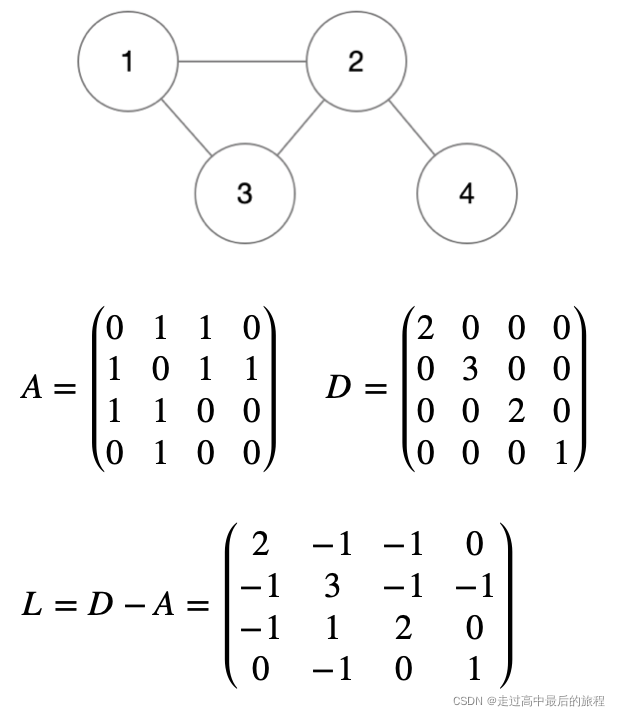
    从这个L矩阵中可以观察到拉普拉斯矩阵的以下几条性质。
    ○ L是对称的
    ○ L是半正定矩阵（每个特征值${\lambda }_i\ge 0$）
    ○ L的每一行每一列的和为0
    ○ L的最小特征值为0。给定一个特征向量$v_0=(1,1,\cdots ,1{)}^T$，根据上一条性质，L的每一行之和为0，所以$L{v}_0=0$

三、拉普拉斯矩阵的推导与意义

3.1 梯度、散度与拉普拉斯算子

    图拉普拉斯矩阵，如果把它看作线性变换的话，它起的作用与分析中的拉普拉斯算子是一样的。我们将在下面详细讨论，这里需要补充一些基础知识：

梯度定义
梯度 “ $\nabla$ ” 是一个矢量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该方向处沿着此梯度方向变化最快，变化率最大（梯度的模）。

    假设一个三元函数$u=f(x,y,z)$在空间区域$G$内具有一阶连续偏导数，点$P(x,y,z)\in G$，则称以下向量表示为点$P$处的梯度：
{ ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z } = ∂ f ∂ x i ⃗ + ∂ f ∂ y j ⃗ + ∂ f ∂ z k ⃗ \{\frac{ {\partial}f}{ {\partial}x},\frac{ {\partial}f}{ {\partial}y},\frac{ {\partial}f}{ {\partial}z}\}=\frac{ {\partial}f}{ {\partial}x}\vec{i}+\frac{ {\partial}f}{ {\partial}y}\vec{j}+\frac{ {\partial}f}{ {\partial}z}\vec{k} { ∂x∂f​,∂y∂f​,∂z∂f​}=∂x∂f​i +∂y∂f​j ​+∂z∂f​k     该式可记为 g r a d f