摘自:腾讯游戏开发精粹(摘录一次加深记忆方便查找, 并未盈利,如有侵权 联系作者删除)
如感兴趣,请购买原书支持 谢谢配合
JPS主体思路:
表现上 JSP算法比A* 快很多, 实际上快到哪里了.我们大概了解一下
A* 会遍历每一个附近的点,然后把符合要求的放到openset列表中,但是 JSP算法 通过一些规则,设置跳点(类似于方向相同,规律相近的点都用跳点表示)的方式,减少需要放入openset列表中的点.减少遍历,减少 需要维护的数据.
所以数据上JPS会比A* 快很多 . 但是 由于 一部分点都用一个点来表示 . 路径表现上 会感觉出寻路出的点 并不是最优路径.
最终, 如果需要实际应用, 寻路出的点列表 需要二次修改, ,经过一些简单的规则,让路径看起来 不那么怪异
**
摘要
**
- 本章介绍跳点搜索(JPS)算法的效率、多线程、内存、路径等优化方法,JPS通过拓展跳点而不是每个邻居来寻路,因为跳点的数目远比邻居少,所以寻路速度远快于A*。
- 本章介绍的效率优化算法用来加速跳点的寻找,或者减少需要拓展的跳点数目。JPS-Bit用位运算加速跳点的寻找,将地图的每个格子编码为1个bit,因此1个int可以存储32个格子。然后利用CPU指令__builtin_clz找到32个格子里的跳点,因此寻找跳点的速度比遍历32个格子快几十倍。JPS-Prune利用剪枝剪掉非必需的“中间跳点”,“中间跳点”在节点拓展中只具有简单的承接作用,不具备拓展价值,剪枝“中间跳点”可以减少需要拓展的跳点数目,从而加速寻路。因为“中间跳点”是路径中沿对角线方向的拐点,找完路径后需要在路径中自行计算“中间跳点”,构成完整路径。JPS-Pre利用预处理提前计算每个格子在上、下、左、右、左上、右上、左下、右下共8个方向的最大step, step为走到最近跳点、阻挡、边界的距离。JPS-Pre无须沿各方向寻找跳点,而是根据预处理的step快速确定跳点,从而加速寻路。
- 三种优化算法可以组合使用,实测中,JPS-Bit、JPS-BitPrune、JPS-BitPre、JPS-BitPrunePre寻路速度分别为A*算法的81倍、110倍、130倍、273倍。另外,将变量声明为thread_local可支持多线程寻路,但每个线程都拥有一个thread_local变量,会导致内存使用量显著增加,需要通过分层、内存池等方法优化内存。JPS寻找的路径在表现上并不是最优的路径,需要通过后处理对路径进行优化。
- JPS算法可以被应用在2D、3D游戏中玩家和NPC的寻路上。2D游戏可以直接应用JPS算法,很多3D游戏也采用2D寻路,因此也可以直接应用该算法。
**
概述
**
-
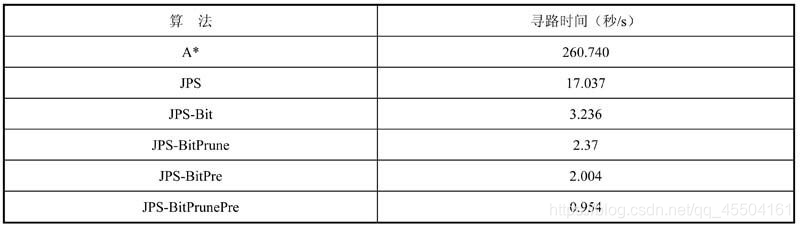
寻路算法在游戏和地图中有多种用途。A*算法已经众所周知,对于其优化也是层出不穷的,然而性能并没有取得突破性进展。本章介绍JPS的效率、多线程、内存、路径等优化算法。在性能实验中设置寻路场景,使得起点和终点差距200个格子,统计寻路10000次的总时间。
-
不同算法的寻路时间如表所示,A*花费260.740s;基础版的JPS花费17.037s;位运算优化的JPS(JPS-Bit)花费3.236s;位运算和剪枝优化的JPS(JPS-BitPrune)花费2.37s;位运算和预处理的JPS(JPS-BitPre)花费2.004s;位运算、剪枝和预处理的JPS(JPS-BitPrunePre)花费0.954s。本章介绍的JPS-Bit和JPS-BitPrune都支持动态阻挡。本章内容解决了绝大部分开源JPS算法存在的潜在Bug:穿越阻挡。
-
实验中,JPS算法的5个版本,平均花费时间分别约为1.7ms、0.32ms、0.23ms、0.2ms、0.095ms,寻路速度分别约为A*算法的15倍、81倍、110倍、130倍、273倍。在2012—2014年举办的三届(目前为止只有三届)基于Grid网格的寻路比赛(The Grid-Based Path Planning Competition, GPPC)中,JPS已经被证明是基于无权重格子,在没有预处理的情况下寻路最快的算法。
-
接下来将介绍JPS的效率、多线程、内存、路径等优化算法。
**
JPS算法
**
1. 算法介绍
JPS(Jump Point Search,跳点搜索)算法是2011年提出的基于Grid网格的寻路算法[1]。JPS算法在保留A算法框架的同时,优化了A算法寻找后继节点的操作。如图9.1所示为A和JPS算法的流程对比,不同于A算法中直接获取当前节点的所有非关闭的可达邻居节点来进行拓展的策略,JPS算法根据当前节点的方向、基于搜索跳点的策略来扩展后继节点,遵循“两个定义、三个规则”(两个定义确定强迫邻居、跳点,三个规则确定节点)的拓展策略。

2. A*算法和JPS算法流程对比
- 2.1 A算法流程, A算法流程如下。
(1)将起点start加入开启节点集合openset中。
(2)重复以下工作:
① 当openset为空时,则结束程序,此时没有路径。
② 寻找openset中F值最小的节点,设为当前节点current。
③ 从openset中移出当前节点current。
④ 在关闭节点集合closedset中加入当前节点current。
⑤ 若current为目标节点goal,则结束程序,由goal节点开始逐级追溯路径上每一个节点x的父节点parent(x),直至回溯到起点start,此时回溯的各节点即为路径。
⑥ 对于current的8个方向的每一个邻居neighbor:如果neighbor不可通过或者已经在closedset中,则略过;如果neighbor不在openset中,则加入openset中;如果neighbor在openset中,若此路径G值比之前路径小,则neighbor的父节点更新为current,并更新G值、F值,G值表示从起点到当前节点的路径代价,H值表示不考虑不可通过区域,从当前节点到终点的路径代价,且F=G+H。
各术语参考如下。
● current:当前节点。
● openset:开启节点集合,集合内节点有待进一步拓展。
● closedset:关闭节点集合,集合内节点不再拓展。
● neighbor:当前节点的邻居。
● parent(x):节点x的父节点。 - 2.2 JSP算法了流程, JPS算法流程如下。
(1)若current当前方向是直线方向:
① 如果current左后方不可走且左方可走(即左方是强迫邻居),则沿current左前方和左方寻找不在closedset中的跳点。
② 如果current当前方向可走,则沿current当前方向寻找不在closedset中的跳点。
③ 如果current右后方不可走且右方可走(右方是强迫邻居),则沿current右前方和右方寻找不在closedset中的跳点。
(2)若current当前方向为对角线方向:
① 如果current当前方向的水平分量可走(例如,current当前方向为东北方向,则水平分量为东,垂直分量为北),则沿current当前方向的水平分量寻找不在closedset中的跳点。
② 如果current当前方向可走,则沿current当前方向寻找不在closedset中的跳点。
③ 如果current当前方向的垂直分量可走,则沿current当前方向的垂直分量寻找不在closedset中的跳点。
3. JPS算法的“两个定义、三个规则”
- 定义一:强迫邻居(Forced Neighbour)。 如果节点n是x的邻居,且节点n的邻居有阻挡,并且parent(x), x, n的路径长度比其他任何从parent(x)到n且不经过x的路径短,其中parent(x)为路径中x的前一个点,则n为x的强迫邻居,x为n的跳点。例如,在图9.2中,寻找从S到E的路径时,K为I的强迫邻居,I为K的跳点。这里不认为从H到K能走,否则会走进H右边的阻挡区,大部分JPS开源代码认为H到K能直接到达,所以存在穿越阻挡的情况。如果需要H到K可走,则K为H的强迫邻居,H为K的跳点。
- 定义二:跳点(Jump Point)。 ① 如果节点y是起点或目标节点,则y是跳点。例如,在图9.2中,S是起点也是跳点,E是目标节点也是跳点。 ② 如果节点y有强迫邻居,则y是跳点,例如I是跳点。 ③ 如果从parent(y)到y为对角线移动,并且y经过水平或垂直方向移动可以到达跳点,则y是跳点。例如,在图9.2中,G是跳点。因为parent(G)为S,从S到G为对角线移动,从G到跳点I为垂直方向移动,I是跳点,所以G也是跳点。
- 规则一:
JPST算法在搜索跳点时,如果直线方向(为了和对角线区分,直线方向代表水平方向和垂直方向,且不包括对角线等斜线方向,下文所说的直线均为水平方向和垂直方向)、对角线方向都可以移动,那么首先在直线方向搜索跳点,然后再在对角线方向搜索跳点。 - 规则二: ① 如果从parent(x)到x为直线移动,n是x的邻居,若有从parent(x)到n且不经过x的路径,且路径长度小于或等于从parent(x)经过x到n的路径,则走到x后下一个点不会走到n。 ② 如果从parent(x)到x为对角线移动,n是x的邻居,若有从parent(x)到n且不经过x的路径,且路径长度小于从parent(x)经过x到n的路径,则走到x后下一个点不会走到n。
- 规则三: 只有跳点才会加入openset中,最后寻找出来的路径点也都是跳点。
4. 算法举例
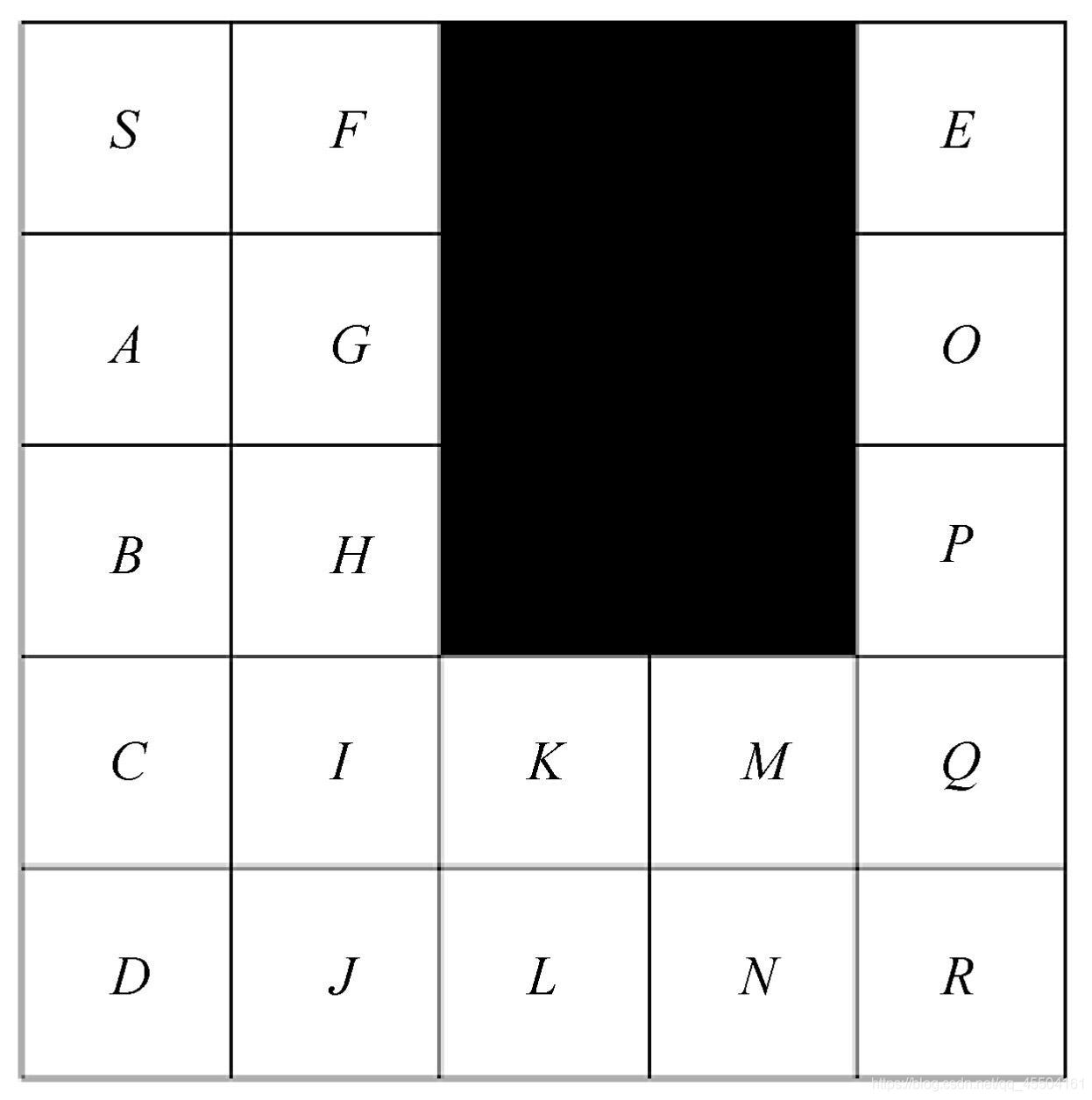
如图所示,5×5的网格,黑色代表阻挡区,S为起点,E为终点,JPS算法寻找从S到E的最短路径。

-
首先将起点S加入openset中。从openset中取出F值最小的点S,并从openset中删除,加入closedset中。S的当前方向为空,则沿8个方向寻找跳点,在该图中从S出发只有下、右、右下3个方向可走,但向下搜索到D遇到边界,向右搜索到F遇到阻挡,因此都没有找到跳点。然后沿右下方向寻找跳点,在G点,根据上文中“定义二”的第3点,parent(G)为S,从parent(G)到S为对角线移动,并且G经过垂直方向移动(向下移动)可以到达跳点I,因此G为跳点并加入openset中。
-
从openset中取出F值最小的点G,并从openset中删除,加入closedset中。G的当前方向为对角线方向(从S到G的方向),沿右(当前方向水平分量)、下(当前方向垂直分量)、右下(当前方向)3个方向寻找跳点。在G点只有向下可走,因此向下寻找跳点,找到跳点I并加入openset中(根据上文中“定义二”的第2点)。
-
从openset中取出F值最小的点I,并从openset中删除,加入closedset中。I的当前方向为直线方向(从G到I的方向),在I点时I的左后方不可走且左方、前方可走,因此沿左方、左前方、前方寻找跳点,但左前方、前方都遇到边界,只有向左方寻找到跳点Q并加入openset中(根据上文中“定义二”的第2点)。
-
从openset中取出F值最小的点Q,并从openset中删除,加入closedset中,Q的当前方向为直线方向,Q 的左后方不可走且左方、前方可走,因此沿左方、左前方、前方寻找跳点,但左前方、前方都遇到边界,只有向左方寻找到跳点E并加入openset中(根据上文中“定义二”的第1点)。
-
从openset中取出F值最小的点E, E是目标节点,寻路结束,路径是S, G, I, Q, E。
注意:这里不考虑从H能走到K的情况,因为对角线方向有阻挡,如果需要H到K能直接到达,则路径是S, G, H, K, M, P,
E,修改跳点的计算方法即可,但在游戏中如果H到K能直接到达,则会穿越H右边的阻挡。 -
上述JPS算法的寻路效率是明显快于A算法的,在从S到A沿垂直方向寻路时,在A点,如果使用A算法,会将F、G、B、H都加入openset中,但是在JPS算法中,这4个点都不会加入openset中。因为S,
A, F的路径长度比S, F路径长,所以从S到F的最短路径不是S, A, F。同理,S, A, G也不是最短路径,根据上文中“规则二”的第1点,走到A后不会走到F、G,所以F、G不会加入openset中。虽然S, A, H是从S到H的最短路径,但是因为存在S, G, H的最短路径且不经过A,根据上文中“规则二”的第1点,从S走到A后,下一个走的点不会是H,因此H也不会加入openset中。根据上文中的“规则三”, B不是跳点,也不会加入openset中。实际上,在从S到E的寻路过程中,进入openset中的只有S、G、I、Q、E。 -
如下图所示为A和JPS算法在寻路消耗中的对比,其中D.Age:Origins、D.Age2、StarCraft分别代表游戏《龙腾世纪:起源》《龙腾世纪2》《星际争霸》的场景图集合;M.Time表示操作openset和closedset的时间;G.Time表示搜索后继节点的时间。可见A算法大约有58%的时间在操作openset和closedset,42%的时间在搜索后继节点;而JPS算法大约有14%的时间在操作openset和closedset,86%的时间在搜索后继节点。避免在openset中加入太多点,从而避免过多地维护最小堆(插入、删除时间复杂度均为O(logn)),是JPS算法比A*快的原因。

5. JSP算法优化
-
5.1 JPS效率优化算法
JPS-Bit通过位运算加速寻找跳点。JPS-Bit和JPS-BitPrune均支持动态阻挡,当动态阻挡出现时,将格子标记为阻挡;当动态阻挡消失时,将格子标记为非阻挡。如下图所示,黑色部分为阻挡,假设当前位置为I,当前方向为右,1代表不可走,0代表可走,则I当前行B的8个格子可用8个bit:00000100表示,I的上一行B-为00000000, I的下一行B+为00110000。用CPU指令__builtin_clz(B)(返回前导0的个数)在B行寻找阻挡的位置,可得当前阻挡在第5个位置(从0开始)。用__builtin_clz(((B->>1) && ! B -)((B+>>1) && ! B+)) 寻找B行的跳点,例如,本例中(B+>>1) && ! B+为(00110000 >> 1) && 11001111,即00001000, (B->>1) &&! B为00000000, __builtin_clz(((B->>1) && ! B -) ||((B+>>1) && ! B+))为__builtin_clz(00001000)为4,所以跳点为第4个位置M。


JPS-BitPrune在JPS-Bit的基础上做剪枝优化,剪掉不必要的中间跳点(见上文中“定义二”的第3点)。中间跳点在节点拓展过程中只具有承接作用,不具备拓展价值,将中间跳点加入openset中会增加拓展的次数,因此JPS-BitPrune将中间跳点全部删除,并将中间跳点的后继跳点的父跳点改为中间跳点的父跳点。JPS-BitPrune需要在找到的路径中加入拐点(中间跳点),使得每两个相邻的路径节点之间都是垂直、水平、对角线方向可达的。假设目前找到的路径为start(jp1), jp2, jp3, …, jpk, end(jpn),对于每两个相邻的跳点jpi、jpi+1:
① 如果jpi、jpi+1的x坐标或者y坐标相等,则说明这两个跳点在同一个水平方向或垂直方向,可以直线到达,无须在这两个跳点之间加入拐点。
② 如果jpi、jpi+1的x坐标和y坐标都不相等,那么:
● 如果x坐标的差dx(即jpi的x坐标减去jpi+1的x坐标)和y坐标的差dy的绝对值相等,则说明这两个跳点在对角线方向直线可达,无须在这两个跳点之间加入中间跳点。
● 如果dx和dy的绝对值不等,则说明这两个跳点在对角线方向不能直线可达,此时在jpi、jpi+1之间就需要加入中间跳点,即jpi沿对角线方向走min(dx, dy)到达的点。如图所示,起点为S(1,1),节点1、4、6均为中间跳点——因为节点2、3是满足“定义二”的跳点,所以节点1是为了到达节点2、3的中间跳点;同理,节点4、6也为中间跳点。在剪枝中间跳点之前,要将中间跳点的后继节点的父节点调整为该中间跳点的父节点。节点1的后继跳点为节点2、3、4,其中节点4也为中间跳点,删掉中间跳点节点1后,节点2、3的父跳点由节点1改为节点S;删除中间跳点节点4后,节点4的后继跳点5的父跳点由节点4改为节点S(节点4的父跳点为节点1,但节点1已经被删除,因此回溯到节点S);删除中间跳点节点6后,节点6的后继跳点7的父跳点由节点6改为节点S(节点6的父跳点为节点4,但节点4已经被删除,节点4的父跳点节点1也被删除了,因此回溯到节点S)。

在寻路中,从节点S寻找跳点,首先找到中间跳点节点1,然后在水平方向和垂直方向寻找到跳点节点2、3,将节点2、3的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点4后,沿水平方向和垂直方向寻找到跳点节点5,将节点5的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点6后,沿水平方向和垂直方向寻找到跳点7,将跳点7的父跳点设为节点S。因此,JPS-BitPrune获得路径S(1,1)、节点7(4,6)。因为路径中S(1,1)无法沿垂直方向、水平方向、对角线方向走到节点7(4,6),需要加入中间拐点。根据上述的拐点添加策略,节点6(4,4)可作为中间拐点。因此,JPS-BitPrune构建的完整路径为S(1,1)、节点6(4,4)、节点7(4,6)。下面通过对比剪枝前后从节点S到节点7的寻路过程,来说明剪枝的优化效率。
不剪枝中间跳点:
(1)从节点S搜索跳点,找到跳点节点1,此时openset中只有节点1。
(2)从openset中取出F值最小的跳点节点1,并搜索节点1的后继跳点,沿水平方向和垂直方向找到跳点节点2、3,沿对角线方向找到跳点节点4,此时openset中有节点2、3、4。
(3)从openset中取出F值最小的跳点节点4,并搜索节点4的后继跳点,沿水平方向和垂直方向找到跳点节点5,沿对角线方向找到跳点6,此时openset中有节点2、3、5、6。
(4)从openset中取出F值最小的跳点节点6,沿垂直方向找到跳点7,此时openset中有节点2、3、5、7。
(5)从openset中取出F值最小的跳点节点7,为目的节点,搜索结束,因此完整路径为节点S(1,1)、节点1(2,2)、节点4(3,3)、节点6(4,4)、节点7(4,6)。剪枝中间跳点:
(1)从节点S寻找跳点,首先找到中间跳点节点1,然后沿水平方向和垂直方向寻找到跳点节点2、3,将节点2、3的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点4后,沿水平方向和垂直方向寻找到跳点节点5,将节点5的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点6后,沿水平方向和垂直方向寻找到跳点7,将跳点7的父跳点设为节点S;继续沿对角线方向寻找跳点,遇到阻挡,搜索终止,此时openset中有节点2、3、5、7。
(2)从openset中取出F值最小的跳点节点7,为目的节点,搜索结束,此时获得的路径为S(1,1)、节点7(4,6)。不同于无剪枝的JPS算法需要拓展中间跳点1、4、6,在JPS-BitPrune中,节点1、4、6作为中间跳点均被剪枝,有效避免了冗余的节点拓展,寻路效率得到大大提升。JPS-BitPre依旧采用JPS-Bit中的位运算,而其中的预处理则是对每个点存储8个方向最多能走的步数step。如果地图大小是N×N,每个方向最多能走的步数用short表示,则存储空间为N×N×8×16bit,如果N为1024,则存储空间为16MB。由于存储空间占用较大,使用JPS-BitPre时需要权衡是否以空间换时间。另外,1024×1024个格子的地图预处理时间在1s内,2048×2048的地图预处理时间为1小时左右。JPS-BitPre和JPS-BitPrunePre都不支持动态阻挡,因为动态阻挡会导致8个方向最多能走的步数发生变化。
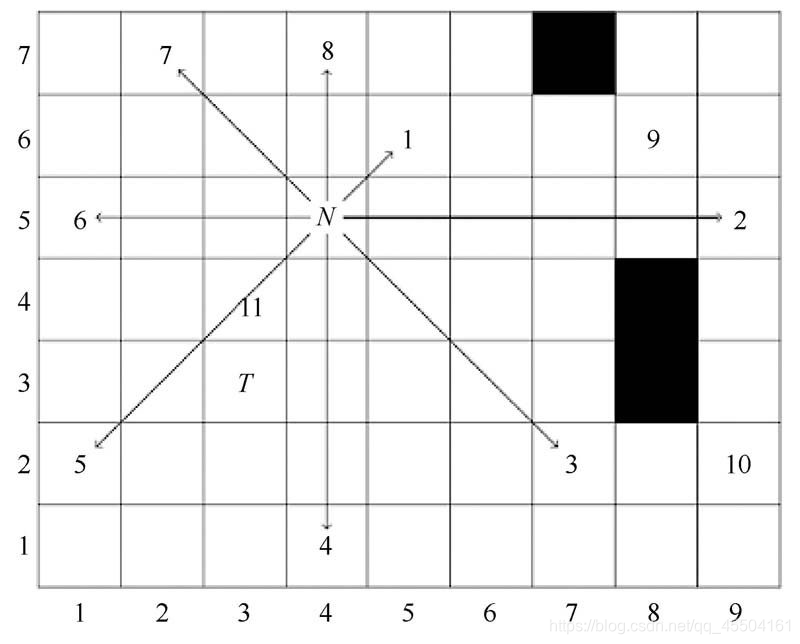
step由跳点、阻挡、边界等决定,如果遇到跳点,则step为走到跳点的步数;否则,step为走到阻挡或边界的步数。例如图9.6中的N点,向上最多走到节点8, step为2;向下最多走到节点4, step为4;向左最多走到节点6, step为3;向右最多走到节点2(节点2是满足“定义二”第2点的跳点), step为5;向左上最多走到节点7, step为2;向右上最多走到节点1(节点1是满足“定义二”第3点的跳点), step为1;向左下最多走到节点5, step为3;向右下最多走到节点3(节点3是满足“定义二”第3点的跳点), step为3。下面通过对比预处理前后从节点N到节点T的寻路过程,来说明预处理的优化效率。
JPS-Bit:
(1)从openset中取出节点N,沿8个方向寻找跳点,节点1、3、11是满足“定义二”第3点的跳点,加入openset中;节点2是满足“定义二”第2点的跳点,加入openset中。
(2)从openset中取出F值最小的节点11,沿垂直方向找到跳点T,加入openset中。
(3)从openset中取出F 值最小的节点T,为目的节点,搜索结束,路径为N(4,5)、节点11(3,4)、节点T(3,3)。JPS-BitPre:
(1)从openset中取出节点N,沿8个方向寻找跳点,根据预处理得到的各方向的step,可以快速确定8个方向最远能到达的节点{1,2,3,4,5,6,7,8},如图9.6所示,节点1、2、3均为满足“定义二”的跳点,直接加入openset中。然后判断终点T位于以N为中心的下方、左下方、左方、左上方、上方的哪部分,因为T位于左下方,只有节点5位于左下方,因此节点4、6、7、8直接略过。在从N到5的方向上,step为3,而N和T的x坐标差绝对值dx为1, y坐标差绝对值dy为2,在从节点N到节点5方向上走min(dx, dy),得到节点11,加入openset中
(2)从openset中取出F值最小的节点11,沿垂直方向找到跳点T,加入openset中。
(3)从openset中取出F 值最小的节点T,为目的节点,搜索结束,路径为N(4,5)、节点11(3,4)、节点T(3,3)。
通过对比发现,JPS-BitPre和JPS-Bit找到的路径是一样的。然而,由于JPS-BitPre无须在每一步节点拓展过程中都沿着各方向寻找跳点,而是根据step快速确定openset的备选节点,从而大大提高了寻路效率。
如图9.7所示,寻路算法无法找到从S到E的路径,失败寻路花费的时间远大于成功寻路花费的时间,因为在失败情况下需要遍历所有的路径。为了避免这种情况,在每次寻路之前,都先判断起点和终点是否可达:如果起点和终点在同一个连通区域,则起点和终点可达,否则不可达。只有起点和终点可达,才需要去寻路。


首先计算Grid网格的连通区域,算法如下:
只能采用宽度优先搜索,深度优先搜索的递归层次太深,会导致栈溢出。如图9.7所示的点S、1、2的连通区域编号均为1,点3、4、E的连通区域编号均为2, S、E连通区域编号不同,因此S、E不在同一个连通区域,不需要寻找路径。
计算连通区域的算法如下。
(1)将当前连通区域编号num初始化为0。
(2)对Grid网格的每个点current重复以下工作:
① num++。
② 如果current是阻挡点,则跳过。
③ 如果current被访问过,则跳过。
④ current的连通区域编号记为num,标记已访问过。
⑤ 宽度优先搜索和current四连通的所有点,连通区域编号均记为num,并标记已访问过。openset采用最小堆实现,最小堆的底层数据结构是一个数组,最小堆的插入、删除、查找时间复杂度均为O(logn)。JPS算法需要频繁在openset和closedset中判断跳点是否存在,因此这里采用以空间换时间的方法对最小堆的查找进行优化,将查找的时间复杂度降为O(1)。
对于1km×1km的地图,构建2000×2000的二维数组matrix,数组的每个元素pnode均为一个指针,指针的对象类型包括节点ID、是否扩展过(expanded,即是否在closedset中)、G值、F值、父跳点指针parent、在最小堆中的索引index等12个字节。如果地图(x, y)处是搜索到的跳点,那么首先检查在matrix(x, y)处指针是否为空,如果为空,则表示该跳点之前未搜索过,从内存池中new出一个跳点,将指针加到最小堆openset中,并在执行shift up、shift down之后,matrix(x, y).index记录跳点在最小堆中的索引;如果不为空,则表示该跳点之前搜索过,首先检查expanded标记,如果标记为真,则表示在closedset中,直接跳过该跳点;否则,如果matrix(x, y)和openset(matrix(x, y).index)的指针相等,则表示在openset中。游戏服务器普遍采用单进程多线程架构,为了支持多线程JPS寻路,需要将一些变量声明为线程独有thread_local。例如,上文中提到的为了优化openset和closedset的查找速度,构建的二维跳点指针数组matrix。该数组必须为线程独有;否则,不同线程在寻路时,都修改matrix元素指向的跳点数据,会导致寻路错误。例如,A线程在扩展完跳点后,将expanded标记为真,B线程再试图扩展该跳点时,发现已经扩展过,就直接跳过。
-
5.2 JPS内存优化
如果采用0.5m×0.5m的格子粒度,每个格子占1bit,则1km×1km的地图占用内存大小约为2000×2000/8字节,即0.5MB。为了在上、下两个方向也能通过取32位数获得32个格子的阻挡信息,需要存储将地图旋转90°后的阻挡信息。上文中不可达两点提前判断,需要存储连通信息,假设连通区域数目最多为15个,则需要内存大小为2000×2000/2字节,即2MB。那么,总内存大小为:原地图阻挡信息0.5MB、旋转地图阻挡信息0.5MB、连通信息2MB,即3MB。
另外,为了优化openset和closedset的查找速度,构建二维跳点指针数组matrix,大小为2000×2000×4字节,即16MB。为了支持多线程,该matrix数组必须为thread_local,16个线程共需内存大小为16×16 MB即256MB,内存空间太大,因此需要优化这部分内存。
首先将2000×2000分成20×20个块,每块为100×100。20×20个块为第一层数组firLayer-Matrix,100×100为第二层数组secLayerMatrix。firLayerMatrix的400个元素为400个指针,每个指针初始化为空,当遍历到的跳点属于firLayerMatrix(x, y)的块时,则从内存池中new出100×100的secLayerMatrix, secLayerMatrix的每个元素也是一个指针,指向从内存池中new出的一个跳点。例如,在搜索2000×2000个格子的地图时,在(231,671)位置找到一个跳点,首先检查firLayerMatrix(2,6)位置的指针是否为空,如果为空,则new出100×100的secLayerMatrix。继续在secLayerMatrix(31,71)处检查跳点的指针是否为空,如果为空,则从内存池中new出跳点,加入openset中;否则,检查跳点的expanded标记,如果标记为真,则表示在closedset中,直接跳过该点;否则表示在openset中。
游戏中NPC寻路均为短距离寻路,因此可以将JPS寻路区域限制为80×80,一个secLayerMatrix是100×100,因此JPS寻路区域可用一个secLayerMatrix表示。那么,两层matrix的大小为:20×20×4字节+100×100×4字节,即0.04MB。在16个线程下,总内存大小为:原地图阻挡信息0.5MB、旋转地图阻挡信息0.5MB、连通信息2MB、两层matrix 0.04MB×16,共3.64MB。游戏中场景最多不到20个,所有场景JPS总内存大小不到72.8MB。
在寻路时,每次将一个跳点加入openset中,都需要new出对应的跳点对象,在跳点对象中存储节点ID、父节点、寻路消耗等共12个字节。为了减少内存碎片,以及降低频繁new的时间消耗,需要自行管理内存池。每次new节点对象时,均从内存池中申请,为了防止内存池增长过大,需要限制搜索步数。内存池是在真正使用内存之前,先申请分配一定数量的、大小相等(一般情况下)的内存块留作备用。当有新的内存需求时,就从内存池中分出一部分内存块,若内存块不够再继续申请新的内存。
这里的内存池共有两个:
(1)跳点的内存池,初始大小为800个跳点,当new出的跳点数目超出800个时,即停止寻路。假设NPC寻路上限距离是20m,则寻路区域面积是40m×40m,格子数目为80×80即6400个,经统计跳点数目占所有格子数目的比例不到1/10,即跳点数目少于640个,因此800个跳点足够使用了,它们共占内存800字节×12,即9.6KB,忽略不计。
(2)secLayerMatrix指向的100×100×4字节的内存池,因为每次寻路都需要至少一个secLayerMatrix,如果每次寻路都重新申请,寻路完后再释放,则会造成开销。因此,secLayerMatrix指向的100×100×4字节的空间也在内存池中,secLayerMatrix内存池占内存0.04MB。 -
5.3 路径优化
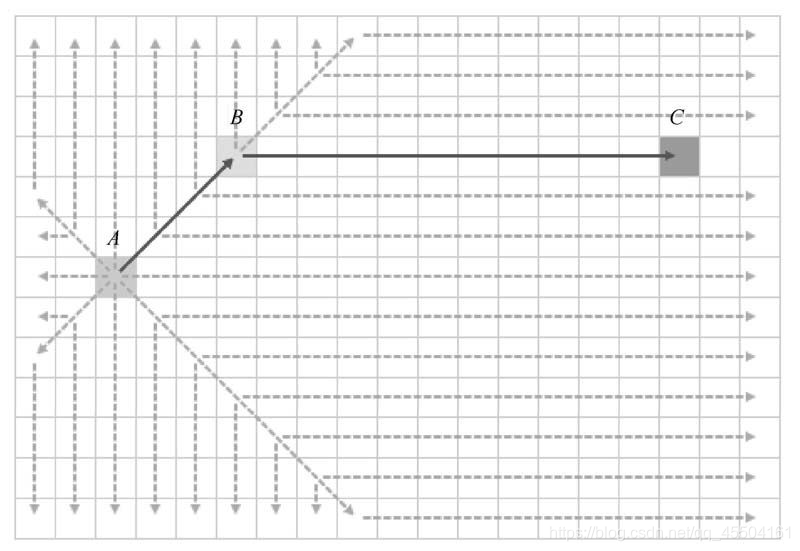
如图所示,A为起点,C为终点,B为跳点,实线为JPS搜索出来的路径,虚线为搜索过程。可以看出,从A到C可以直线到达,而JPS搜索出来的路径却需要转折一次,在游戏表现上,会显得比较奇怪。因此,在JPS搜索出来路径后,需要在表现上对路径进行优化。比如JPS搜索出来的路径有A、B、C、D、E、F、G、H 8个点,走到A时,需要采样检查A、C是否直线可达,如果A、C直线可达,再检查A、D是否直线可达,如果A、D直线可达,则继续检查A、E,如果A、E直线不可达,则路径优化为A, D, E, F, G, H;走到D时,再检查D、F是否直线可达,如果D、F直线可达,则继续检查D、G,如果D、G直线不可达,则路径优化为A, D, F, G, H。依此类推,直到走到H。因为采样检查的速度很快,大约占JPS寻路时间的1/5,而且只有当走到一个路点后,才采样检查该路点之后的路点是否可以合并,将采样的消耗平摊在行走的过程中,因此采样的消耗可以忽略。








 本文深入探讨了JPS算法在游戏开发中的应用与优化,包括效率、多线程、内存和路径优化方法,通过对比A*算法,展示了JPS算法在寻路速度上的显著优势。
本文深入探讨了JPS算法在游戏开发中的应用与优化,包括效率、多线程、内存和路径优化方法,通过对比A*算法,展示了JPS算法在寻路速度上的显著优势。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








