线性规划 - 数学建模

一、线性规划模型及概念

规划问题的数学模型一般由三个因素构成 决策变量 目标函数 约束条件
数学规划是运筹学的一个重要分支，线性规划是数学规划的一个重要分支
线性规划即以线性函数为目标函数，线性条件为约束条件

建立线性规划模型的基本步骤
（1）分析问题，找出决策变量
（2）根据问题，找出决策变量必须满足的一组线性等式或者不等式约束，即为约束条件
（3）根据问题的目标，构造关于决策变量的一个线性函数，即为目标函数

二、线性规划模型求解及应用

1、基于求解器求解

标准形式如下

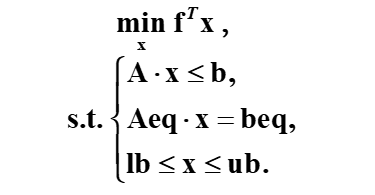
解法：

[x, fval, exitflag, output, lambda] = linprog(f, A, b, Aeq, beq, lb, ub, options)

其中，
输入参数：
f 为系数向量，表示目标函数系数，列向量；
A 为线性不等式约束矩阵，A 表示约束中的线性系数；
b 为线性不等式约束向量，b 表示约束中的常向量；
Aeq 为线性等式约束矩阵，beq 为线性等式约束向量；
lb 为下界，ub 为上界；
options 为 linprog 的选项
输出参数：
x 为解，fval 为目标函数最优值；
exitflag 为算法停止条件，output 为求解过程摘要，lambda 为解处的拉格朗日乘数

2、基于问题求解

首先需要用变量和表达式构造优化问题，然后用solve函数求解，详见例题

三、例题

求解下列线性规划问题

1、基于求解器求解

化为标准型

clc, clear, f = [-2; -3; 5];
a = [-2, 5, -1; 1, 3, 1]; b = [-10; 12];
aeq = [1, 1, 1]; beq = 7;
[x, y] = linprog(f, a, b, aeq, beq, zeros(3, 1));
x, y = -y  %目标函数最大化

2、基于问题求解

clc, clear
prob = optimproblem('ObjectiveSense', 'max');  % 'ObjectiveSense'为优化的意义，默认求最小
x = optimvar('x', 3, 'LowerBound', 0); % name为变量名称，n为变量维度，cstr为索引名称，Type为变量类型，continuous（默认实数）或integer（整数），LowerBound为下界，UpperBound为上界
prob.Objective = 2 * x(1) + 3 * x(2) - 5 * x(3); % .Objective为目标函数
prob.Constraints.con1 = x(1) + x(2) + x(3) == 7; % .Constraints.con1为约束条件
prob.Constraints.con2 = 2 * x(1) - 5 * x(2) + x(3) >= 10;
prob.Constraints.con3 = x(1) + 3 * x(2) + x(3) <= 12;
[sol, fval, flag, out] = solve(prob), sol.x % sol.x为优化变量矩阵，fval为目标函数最优值

求得的最优解为 x1 = 6.4286, x2 = 0.5714, x3 = 0, 对应的最优值为 z = 14.5714