最长公共子串LCS

CSDN话题挑战赛第2期
参赛话题：学习笔记

最长公共子串LCS

最长公共子串LCS的全称是：Longest Common Substring，它是解决字符串匹配问题的常见算法，我们可以举个简单的栗子：

一、问题描述

例如我们有两条字符串：
S1 = I love natural language processing
S2 = natural language loves me too
那么，对于S1和S2的最长公共子串我们一眼就能可看出来是：natural language，但是对于计算机来说，需要计算最长公共子串的长度以及输出最长公共子串，该怎么办呢？

二、算法描述

动态规划成为我们解决该问题的首选

（一）设计状态

我们用f[i][j] 表示序列Si = {x1,x2,…,xi} 与 序列Sj = {x1,x2,…,xj} 的最长公共子串的长度。

（二）状态转移方程

怎么理解这个状态转移方程呢？我们可以通过一个表格来掌握

以：IloveNLP和NLPlovesme为例；
首先，若i = 0 或者j = 0 表示其中有一个串为空串，那么自然而然，总的f[i][j] = 0 ，最长公共子串的长度为0；
若xi = yj ，那么f[i][j] = 1 + f[i-1][j-1]，也就是该项的左上角那一项的值加1；
若xi ！= yj ，那么f[i][j] = max { f[i-1][j] ，f[i][j-1] }，也就是取该项的左侧和上侧的最大值。
那么最终得到，最长公共子串的长度为4，长度求出来了，但还有一个问题
最长公共子串是什么呢？

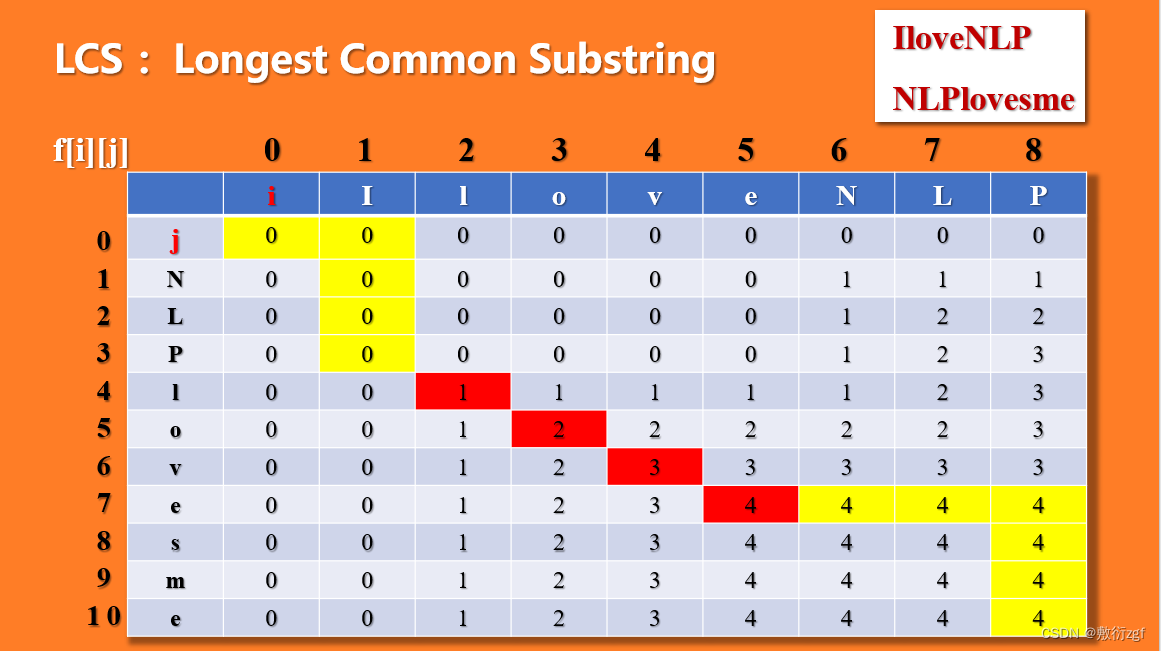
从右下端的 4 出发，4是由左侧和上方的最大值推导而来，但此时左侧和上方的取值相等，因此我们规定一个方向，以向上为例，将其标黄；一直到f[6][7]，f[6][7]是由f[5][7]推导而来，而f[5][7]对应的xi = yj ，因此它是最长公共子串的一部分，将其标红，按照此规则，一直到头，找到全部的最长公共子串：love

三、算法实现

def max_common_s(s1, s2):
    chart = [[0 for i in range(len(s1)+1)]for j in range(len(s2)+1)]            #建立一个二维数组
    for i in range(1, len(s2)+1):
        for j in range(1, len(s1)+1):       
            if s1[j-1] == s2[i-1]:                                          #如果对应的两个值相等，则其左上方的值加1
                chart[i][j] = chart[i-1][j-1]+1
            else:
                chart[i][j] = max(chart[i-1][j], chart[i][j-1])             #要是不相等，则取其右方或上方的最大值
#     print(chart) # 输出状态矩阵
    return chart

def find_one(chart, s1, s2):
    max_str = ''
    i = len(s1)
    j = len(s2)
    while i > 0 and j > 0:
        print(s1[i-1])
        print(s2[j-1])
        print("=====")
        if s1[i-1] == s2[j-1]:   #这里之所以从最后一个字符开始比较，是因为看表格  若最后一个字符相等，则一定来自于左上方
            max_str += s1[i-1]
            i -= 1
            j -= 1
        else:  # 不等，就一定来自左侧或者上侧的最大值
            if chart[j][i-1] > chart[j-1][i]:           #若左边的数字较大，则来自左边
                i -= 1
            else:                                       #否则来自上方
                j -= 1
    return reversed(max_str)                            #逆序输出


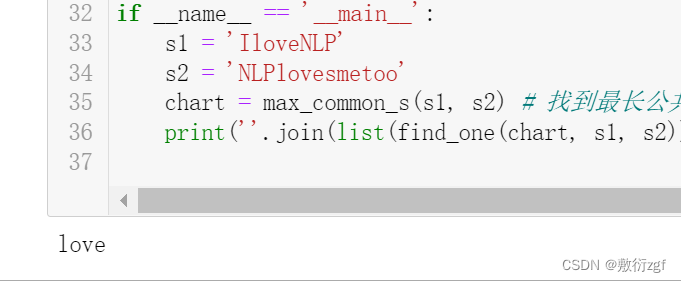
if __name__ == '__main__':
    s1 = 'IloveNLP'
    s2 = 'NLPlovesmetoo'
    chart = max_common_s(s1, s2) # 找到最长公共子串
    print(''.join(list(find_one(chart, s1, s2)))) # 将最长公共子串的每一个字符连接在一起