OpenFOAM——SIMPLE,PISO,PIMPLE

xzzzzzhao

已于 2023-02-24 16:14:07 修改

阅读量310

点赞数

分类专栏： OpenFOAM 文章标签：算法

于 2023-02-24 15:42:48 首次发布

本文链接：https://blog.csdn.net/qq_45682183/article/details/129202089

版权

OpenFOAM 专栏收录该内容

4 篇文章 5 订阅

订阅专栏

SIMPLE & PISO &PLMPLE

参考链接
不可压缩连续性方程和动量方程为：

$\begin{aligned} &\nabla \cdot \mathbf{u} = 0 \\ &\frac{\partial \mathbf{u}}{\partial t} +\nabla \cdot(\mathbf{u}\mathbf{u})-\nabla\cdot(\nu \nabla \mathbf{u}) = -\nabla p \end{aligned}$

下面利用连续性方程与动量方程推到压力方程。

离散线性化动量方程，同时压力梯度的形式保持不变。得到：

$\left[ \begin{matrix} a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & \cdots & a_{3,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & a_{n,3} & \cdots & a_{n,n} \\ \end{matrix} \right] \left[\begin{matrix} u_1 \\ u_2 \\ u_3 \\ \vdots \\ u_n \end{matrix}\right]= \left[\begin{matrix} r_1 \\ r_2 \\ r_3 \\ \vdots \\ r_n \end{matrix}\right]+ \left[\begin{matrix} (\partial p/\partial x)_{1} \\ (\partial p/\partial x)_{2} \\ (\partial p/\partial x)_{3} \\ \vdots \\ (\partial p/\partial x)_{n} \end{matrix}\right]$

$\underbrace{\left[ \begin{matrix} a_{1,1} & 0 & 0 & \cdots & 0 \\ 0 & a_{2,2} & 0 & \cdots & 0 \\ 0 & 0 & a_{3,3} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{n,n} \\ \end{matrix} \right]}_{\text{Diagonal}~\mathbf{A}} \left[\begin{matrix} u_1 \\ u_2 \\ u_3 \\ \vdots \\ u_n \end{matrix}\right]+ \underbrace{\left[ \begin{matrix} 0 & a_{1,2} & a_{1,3} & \cdots & a_{1,n} \\ a_{2,1} & 0 & a_{2,3} & \cdots & a_{2,n} \\ a_{3,1} & a_{3,2} & 0 & \cdots & a_{3,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & a_{n,3} & \cdots & 0 \\ \end{matrix} \right]}_{\text{Off diagonal}} \left[\begin{matrix} u_1 \\ u_2 \\ u_3 \\ \vdots \\ u_n \end{matrix}\right]= \left[\begin{matrix} r_1 \\ r_2 \\ r_3 \\ \vdots \\ r_n \end{matrix}\right]+ \left[\begin{matrix} (\partial p/\partial x)_{1} \\ (\partial p/\partial x)_{2} \\ (\partial p/\partial x)_{3} \\ \vdots \\ (\partial p/\partial x)_{n} \end{matrix}\right]$

$a_P^{\mathrm{u}} \mathbf{u}_P+\sum_N a_N^{\mathrm{u}} \mathbf{u}_N=\mathbf{r}-\nabla p$

其中， $r$ 是源项。

引入 $\mathbf{H}(\mathbf{u})$ ：

$\mathbf{H}(\mathbf{u})=\mathbf{r}-\sum_{N}a_{N}^{\mathbf{u}}\mathbf{u}_{N}$

因此：

$\begin{aligned} a_{P}^{\mathbf{u}}\mathbf{u}_{P} & = \mathbf{H}(\mathbf{u})-\nabla p \\ \mathbf{u}_{P} & = (a_{P}^{\mathbf{u}})^{-1} (\mathbf{H}(\mathbf{u})-\nabla p) \end{aligned}$

将连续性方程代入即得到压力方程：

$\nabla \cdot\left[\left(a_P^{\mathrm{u}}\right)^{-1} \nabla p\right]=\nabla \cdot\left[\left(a_P^{\mathrm{u}}\right)^{-1} \mathbf{H}(\mathbf{u})\right]$
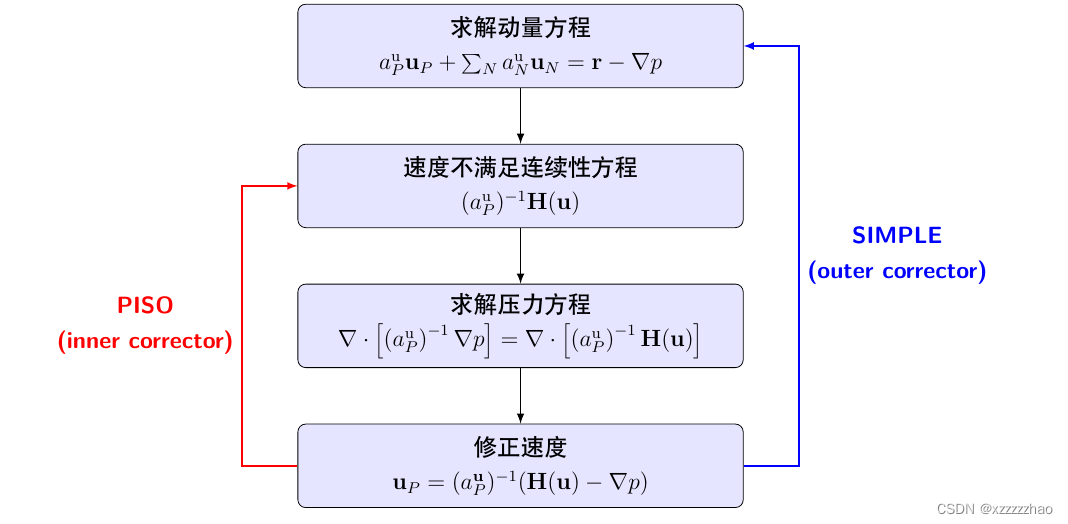
SIMPLE PISO PIMPLE

SIMPLE算法并未考虑算子 $\mathbf{H}(\mathbf{u})$ 是由不满足连续性方程的速度构造得到的。SIMPLE回到循环的开始，并在时间上进行(迭代)。
PISO算法返回对 $\mathbf{H}(\mathbf{u})$ 的修正并且再次执行动量校正步骤，然后进行时间上的迭代。
PIMPLE算法是SIMPLE(outer corrector)算法与PISO(inner corrector)算法的融合.主要思想是在每个时间步长中寻求一个完全收敛的稳态解，并在时间上进行。如果只进行一个外部修正循环与多个内部循环，PIMPLE循环类似于PISO。在每个时间步长中，可以使用欠松弛来实现平稳收敛。