CUDA编程-矩阵乘法和用共享内存优化

最新推荐文章于 2025-10-24 22:41:36 发布

原创最新推荐文章于 2025-10-24 22:41:36 发布 · 817 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #人工智能

CUDA编程-矩阵乘法和用共享内存优化

矩阵乘法
如果是使用C++进行矩阵乘法的计算，我们应该都知道，就是串行的枚举每个元素，然后计算对应的C[i][j]。对于用GPU来计算矩阵乘法来说，我们就是通过很多线程并行的计算每一个C[i][j]，每个线程只负责一个对应位置元素。
代码

#include <stdio.h>

// these are just for timing measurments
#include <time.h>

// error checking macro
#define cudaCheckErrors(msg) \
    do { \
        cudaError_t __err = cudaGetLastError(); \
        if (__err != cudaSuccess) { \
            fprintf(stderr, "Fatal error: %s (%s at %s:%d)\n", \
                msg, cudaGetErrorString(__err), \
                __FILE__, __LINE__); \
            fprintf(stderr, "*** FAILED - ABORTING\n"); \
            exit(1); \
        } \
    } while (0)


const int DSIZE = 8192;
const int block_size = 32;  // CUDA maximum is 1024 *total* threads in block
const float A_val = 3.0f;
const float B_val = 2.0f;

// matrix multiply (naive) kernel: C = A * B
__global__ void mmul(const float *A, const float *B, float *C, int ds) {

  int idx = threadIdx.x+blockDim.x*blockIdx.x; // create thread x index
  int idy = threadIdx.y+blockDim.y*blockIdx.y; // create thread y index

  if ((idx < ds) && (idy < ds)){
    float temp = 0;
    for (int i = 0; i < ds; i++)
      temp += A[idy*ds+i] * B[i*ds+idx];   // dot product of row and column
    C[idy*ds+idx] = temp;
  }
}

int main(){

  float *h_A, *h_B, *h_C, *d_A, *d_B, *d_C;


  // these are just for timing
  clock_t t0, t1, t2;
  double t1sum=0.0;
  double t2sum=0.0;

  // start timing
  t0 = clock();

  h_A = new float[DSIZE*DSIZE];
  h_B = new float[DSIZE*DSIZE];
  h_C = new float[DSIZE*DSIZE];
  for (int i = 0; i < DSIZE*DSIZE; i++){
    h_A[i] = A_val;
    h_B[i] = B_val;
    h_C[i] = 0;}

  // Initialization timing
  t1 = clock();
  t1sum = ((double)(t1-t0))/CLOCKS_PER_SEC;
  printf("Init took %f seconds.  Begin compute\n", t1sum);

  // Allocate device memory and copy input data over to GPU
  cudaMalloc(&d_A, DSIZE*DSIZE*sizeof(float));
  cudaMalloc(&d_B, DSIZE*DSIZE*sizeof(float));
  cudaMalloc(&d_C, DSIZE*DSIZE*sizeof(float));
  cudaCheckErrors("cudaMalloc failure");
  cudaMemcpy(d_A, h_A, DSIZE*DSIZE*sizeof(float), cudaMemcpyHostToDevice);
  cudaMemcpy(d_B, h_B, DSIZE*DSIZE*sizeof(float), cudaMemcpyHostToDevice);
  cudaCheckErrors("cudaMemcpy H2D failure");

  // Cuda processing sequence step 1 is complete

  // Launch kernel
  dim3 block(block_size, block_size);  // dim3 variable holds 3 dimensions
  dim3 grid((DSIZE+block.x-1)/block.x, (DSIZE+block.y-1)/block.y);
  mmul<<<grid, block>>>(d_A, d_B, d_C, DSIZE);
  cudaCheckErrors("kernel launch failure");

  // Cuda processing sequence step 2 is complete

  // Copy results back to host
  cudaMemcpy(h_C, d_C, DSIZE*DSIZE*sizeof(float), cudaMemcpyDeviceToHost);

  // GPU timing
  t2 = clock();
  t2sum = ((double)(t2-t1))/CLOCKS_PER_SEC;
  printf ("Done. Compute took %f seconds\n", t2sum);

  // Cuda processing sequence step 3 is complete

  // Verify results
  cudaCheckErrors("kernel execution failure or cudaMemcpy H2D failure");
  for (int i = 0; i < DSIZE*DSIZE; i++) if (h_C[i] != A_val*B_val*DSIZE) {printf("mismatch at index %d, was: %f, should be: %f\n", i, h_C[i], A_val*B_val*DSIZE); return -1;}
  printf("Success!\n"); 
  return 0;
}

在这份代码上，我只有一点是想说。我们使用的是指针分配空间的方式来存储矩阵，也就是说用一维的方式存储矩阵，所以其实在使用的过程中，我们要时常的进行一维和二维的转换，所以会很容易弄乱。

  int idx = threadIdx.x+blockDim.x*blockIdx.x; // create thread x index
  int idy = threadIdx.y+blockDim.y*blockIdx.y; // create thread y index

这段代码计算出全局中线程的x和y坐标，计算这个是为了用这个线程来计算
C[i][j]的值。我们知道在矩阵乘法中，计算C[i][j]的方式是：
$∑k=0k=nC[i][j]=A[i][k]∗B[k][j]\sum_{k=0}^{k=n} C[i][j]=A[i][k]*B[k][j]$
所以在每个线程中，我们都需要有一个n次的循环来计算每个C[i][j]，对于这里，有一个小技巧，如果我们直接通过前面得到的线程索引 $i d x$ 和 $i d y$ 来计算一维的 $A [i] [k]$ 和 $B [k] [j]$ 会有一些乱，我们可以这样。

if ((idx < ds) && (idy < ds)){
    float temp = 0;
    for (int i = 0; i < ds; i++)
      /*
      A_x=idy
      A_y=k
      A[idy*ds+k]
      B_x=k
      B_y=idx
      B[k*ds+idx]
      */
      temp += A[idy*ds+i] * B[i*ds+idx];   // dot product of row and column
    C[idy*ds+idx] = temp;
  }

遇到的小问题
当时在练习矩阵乘法的时候，我其实是按照C[idx][idy]来计算的，但是我经过测试发现，如果是按照C[idx][idy]来计算每个C点的值，最后运行时间比用C[idy][idx]慢的多，后来发现了原因。
CUDA中的全局内存访问是按行主序存储的，这意味着同一行的元素在内存中是连续存储的，所以如果我们按行访问数据的时间应该是更快的。那不就是说明C[idx][idy]这种方式访问的更快吗？因为这种方式是通过行来访问的，但是后来我发现，在计算索引的时候，idx和idy和我们平时的使用是相反的。
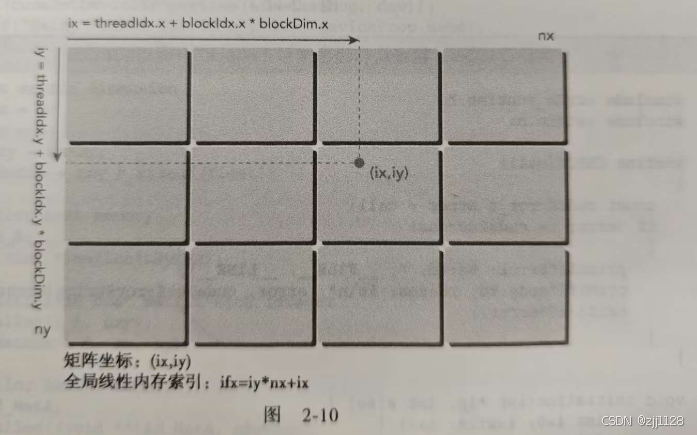
在这里插入图片描述

所以说C[idy][idx]才是符合我们的按行访问数据的。
共享内存
按我的理解，共享内存就是在芯片上的，所以使用共享内存访问数据会比全局内存会快很多，而且共享内存的这个共享是线程块内的共享，也就是说不同块之间的共享内存是不能相互通信的，里面的数据内容也是不同的。
好了接下来我们解释一下为什么可以使用共享内存来优化矩阵乘法，刚开始的时候想了好久都没有理解这个过程，接下来我会用一个例子来解释这个问题。

a00 a01 a02 a03      b00 b01 b02 b03      c00 c01 c02 c03
a10 a11 a12 a13  *   b10 b11 b12 b13  =   c10 c11 c12 c13
a20 a21 a22 a23      b20 b21 b22 b23      c20 c21 c22 c23
a30 a31 a32 a33      b30 b31 b32 b33      c30 c31 c32 c33

这是一个4×4矩阵的例子，用这个例子可以扩展到很大的矩阵。
假设我们的块是block(2,2),也就是一个块里面有四个线程，也就是说我们一个线程块里面可以算出四个点的值，我们现在盯着线程块block(1,0)，也就是要计算这四个点的数据：

c20 c21
c30 c31

如果从分块的角度来看：

A00  A01        B00  B01        C00  C01
          *                 =
A10  A11        B10  B11        C10  C11
所以分块矩阵C10的计算公式:
C10=A10*B00+A11*B10

也就是说计算C10这个分块矩阵的线程块需要分块矩阵A10 B00 A11 B10，像这些重复使用的数据，我们就可以存储在分块矩阵中，因为是相加的，所以第一次我们共享内存中就存储A10和B00，然后第二次共享内存中就存储A11和B10，也就是这样：

  for (int i = 0; i < ds/block_size; i++) {

      // Load data into shared memory
      As[threadIdx.y][threadIdx.x] = A[idy * ds + (i * block_size + threadIdx.x)];
      Bs[threadIdx.y][threadIdx.x] = B[(i * block_size + threadIdx.y) * ds + idx];

      // Synchronize
      __syncthreads();

      // Keep track of the running sum
      for (int k = 0; k < block_size; k++)
      	temp += As[threadIdx.y][k] * Bs[k][threadIdx.x]; // dot product of row and column
      __syncthreads();

    }

像ds/block_size这个循环次数就是我们对大矩阵进行分块以后，进行矩阵乘法的时候，需要有几项相加，所以就需要循环几次，这样得到的值就是最终的值。
小问题
我还想说的一点是

  As[threadIdx.y][threadIdx.x] = A[idy * ds + (i * block_size + threadIdx.x)];
  Bs[threadIdx.y][threadIdx.x] = B[(i * block_size + threadIdx.y) * ds + idx];