专转本微分方程

变量可分离方程

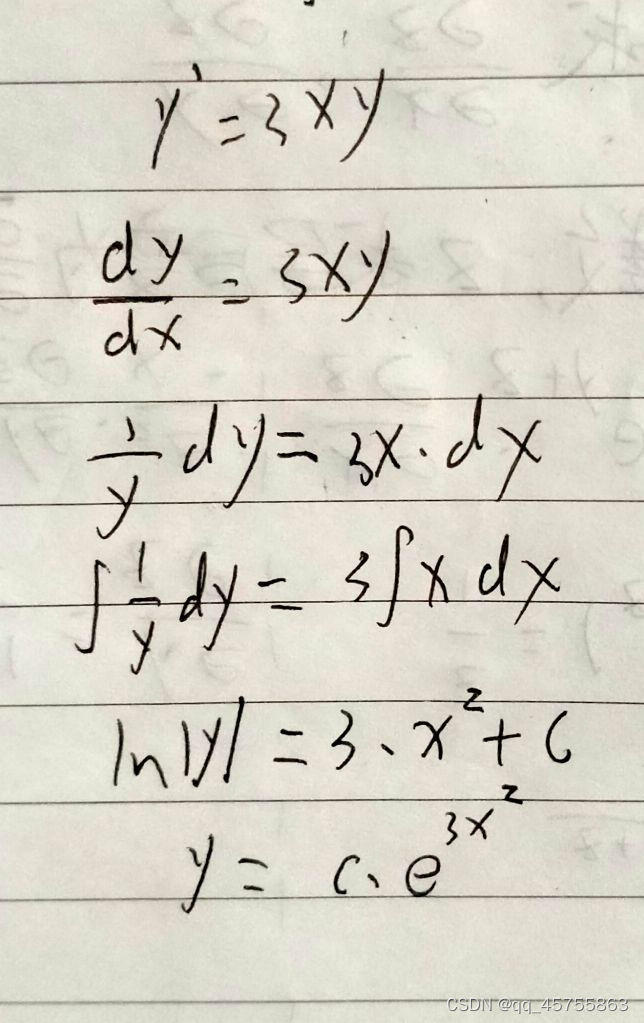
齐次方程

1. $将方程化为\frac{dy}{dx}=\phi (\frac{y}{x})$
2. $换元，令u=\frac{y}{x},则y=xu,y^{\prime }=u+x{u}^{\prime },就是\frac{dy}{dx}=u+x\frac{dy}{dx}，将u=\frac{y}{x}、\frac{dy}{dx}=u+x\frac{dy}{dx}带回方程\frac{dy}{dx}=\phi (\frac{y}{x})$
3. $分离变量，就是x\frac{dy}{dx}=u$

习题

一阶线性非齐次方程

y’+P(x)y=Q(x)
$$y=e^{\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+c]主要就是这个公式$$

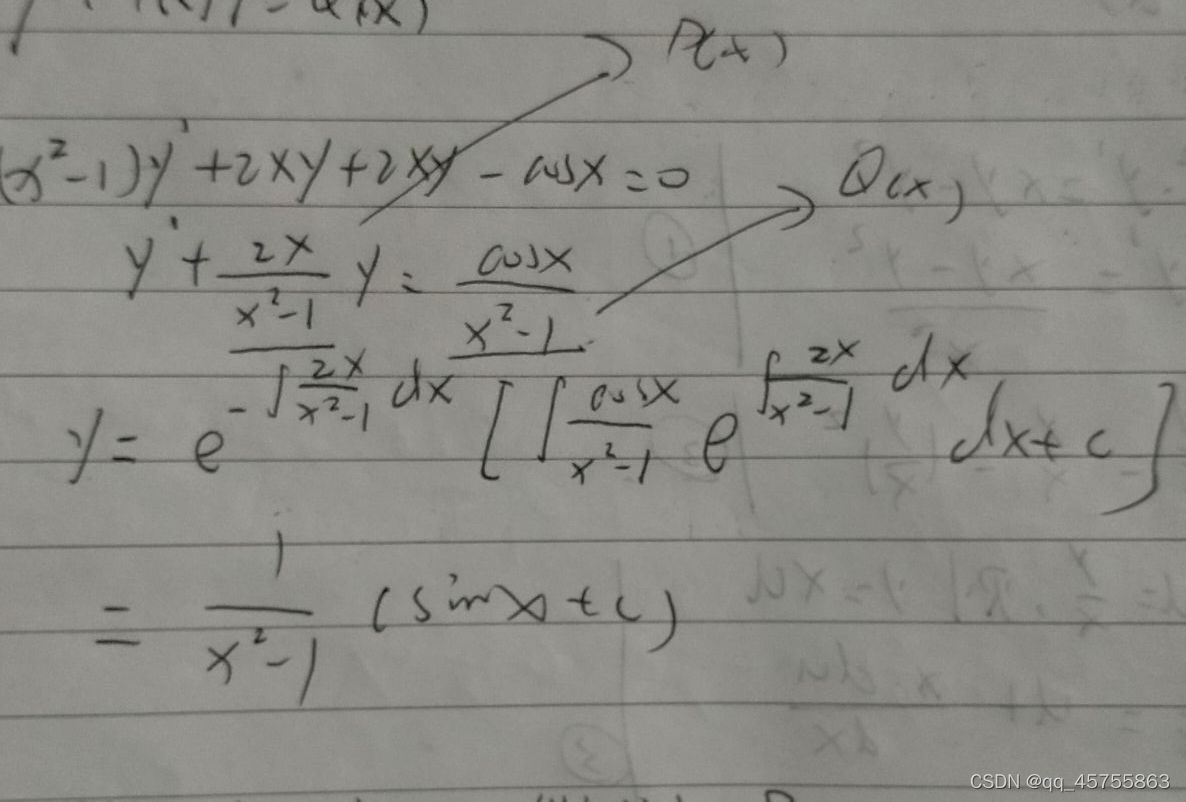
二阶常系数微分方程

二阶常系数线性齐次方程ay’’+by’+cy=0

这个根就是特征方程和特征根

有两个不相等实数根$r_1\ne r_2$	$y=c_1{e}^{r_{1}x}+c_2{e}^{r_{2}x}$
有两个相等实数根$r_1=r_2$	$y=(c_1+c_{2}x)e^{r_{1}x}$
有两个复根$r_{1,2}=\alpha \pm \beta i$	$y=e^{ax}(c_{1}cos\beta +c_{2}sin\beta )$

习题

二阶常系数线性非齐次方程$a{y}^{\prime \prime }+b{y}^{\prime }+cy=f(x)$

这种的关键点在于y*的特解设法
一般而言这个$y^{\ast }=x^k+Q(x)e^{ax}$
k的值在于α同m,n是否相等，全等就是二重特征根，一个就是单特征根，没有就不是特征根
α同原方程一致
Q(x)取决于原方程是一次函数，还是二次函数以及常数

已知特解求通解（去年和前年都考过了）

$己知函数y=e^x和y=e^{-2x}的二阶常系数线性微分方程y^{\prime }+p{y}^{\prime }+qy=e^x两个解,试确定p,q的值，并求微分方程y^{\prime }+p{y}^{\prime }+qy=e^x的通解。$

微分方程得几何应用

求一过点（1,-1)的曲线，使其上任一点处的切线夹于两坐标轴向的线段被
切点平分.
=y’(X-X），
在曲线上任取一点p(x,y)，则p点处的切线方程为$\overline{Y}$-y=y’(X-x)
令Y=0，得切线在X轴上的截距X=x-$\frac{y}{y^{\prime }}$
令X=0，得切线在Y轴上截距Y=y-xy’，
$$依题意有f(x,y)=\{\begin{array}{r}x=\frac{X+0}{2}=\frac{x}{2}-\frac{y}{2y^{\prime }}(x,y)\ne 0\\ y=\frac{Y+0}{2}=\frac{Y}{2}-\frac{x{y}^{\prime }}{2}x=0\end{array}即x{y}^{\prime }=-y且y(1)=-1$$
分离变量两边积分得微分方程通解力lny = -lnx+ Inc$\to$xy=c，由y(1)=-1可得c=-1就是xy=-1
下面是以前我不会的