背包问题的n种解法

背包问题

有n个重量和价值分别为wi,vi的物品，从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和的最大值。

示例：
n=3
{w,v}={{1,3},{2,4},{2,2}}
W=4

1.深度优先遍历

(i, j) 表示搜索到第i个物品时的重量剩余j
其中搜索到第i个物品时有挑选和不挑选两种选择，从而形成二叉树
利用二叉树将所有可能性列举出来，从而递归进行深度优先遍历得到最优解

时间复杂度：O(2^n)

#include"stdio.h"
#include"stdlib.h"
#include"algorithm"
using namespace std;
#define MAX 100

int n, w;
int a[MAX], b[MAX];//物品重量a,物品价值b

int rec(int i, int j) {
	//当搜索完所有的物品后结束
	if (i == n)
		return 0;
	//当第i个物品的重量超出剩余重量时跳过
	else if (a[i] > j)
		return rec(i + 1, j);//在挑选和不挑选中选择最优方案
	else {
		return max(rec(i + 1, j), rec(i + 1, j - a[i]) + b[i]);
	}
}

int main() {
	scanf_s("%d%d", &n, &w);
	for (int i = 0; i < n; i++) {
		scanf_s("%d", &a[i]);
		scanf_s("%d", &b[i]);
	}
	printf("%d", rec(0, w));
	system("pause");
}

2.记忆化搜索

上图黄色边框圈起来的节点相同，这些相同的节点在深度优先遍历中会多次计算，因而设立记忆化数组来存放节点数据，便可减少类似的浪费，从而降低时间复杂度，参数的组合由nW种，

因此时间复杂度为O(nW)

#include"stdio.h"
#include"stdlib.h"
#include"algorithm"
using namespace std;
#define MAX 100

int n, w;
int a[MAX], b[MAX];
int dp[MAX][MAX];

int rec(int i, int j) {
    //当某节点被计算过直接返回值
	if (dp[i][j] > -1) {
		return dp[i][j];
	}
	int res;
	if (i == n)
		res = 0;
	else if (a[i] > j)
		res = rec(i + 1, j);
	else {
		res = max(rec(i + 1, j), rec(i + 1, j - a[i]) + b[i]);
	}
	dp[i][j] = res;
	return res;
}

int main() {
	scanf_s("%d%d", &n, &w);
	for (int i = 0; i < n; i++) {
		scanf_s("%d", &a[i]);
		scanf_s("%d", &b[i]);
	}
	//初始化数组
	memset(dp, -1, sizeof(dp));
	printf("%d", rec(0, w));
	system("pause");
}

3.动态规划

首先了解动态规划的要素：①初始数据 ②基于初始数据的递归规律

1.基于上述记忆化搜索的逆序动态规划

int rec(int i, int j) {
	//当搜索完所有的物品后结束
	if (i == n)
		return 0;
	//当第i个物品的重量超出剩余重量时跳过
	else if (a[i] > j)
		return rec(i + 1, j);
		//在挑选和不挑选中选择最优方案
	else {
		return max(rec(i + 1, j), rec(i + 1, j - a[i]) + b[i]);
	}
}

初始数据：dp[n][j]=0；
递推式：
$$dp[i][j]=\{\begin{array}{ll}dp[i+1][j]& \text{当a[i]>j}\\ max(dp[i+1][j],dp[i+1][j-a[i]]+b[i]）& \text{其他}\end{array}$$

得出dp数组

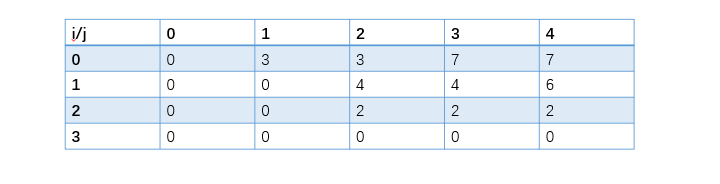
时间复杂度为O(nW)

#include"stdio.h"
#include"stdlib.h"
#include"algorithm"
using namespace std;
#define MAX 100

int n, w;
int a[MAX], b[MAX];
int dp[MAX][MAX];

void solve() {
	for (int i = 0; i <= w; i++)
		dp[n][i] = 0;
	for (int i = n - 1; i >= 0; i--) 
		for (int j = 0; j <= w; j++) {
			if (a[i] > j)  dp[i][j] = dp[i + 1][j];
			else dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - a[i]] + b[i]);
		}
}

int main() {
	scanf_s("%d%d", &n, &w);
	for (int i = 0; i < n; i++) {
		scanf_s("%d", &a[i]);
		scanf_s("%d", &b[i]);
	}
	solve();
	printf("%d", dp[0][w]);
	system("pause");
}

2.顺序动态规划

dp[i][j]表示当选择完序号为0,1，……i-1的物品后当前的价值
因此初始dp[0][j]还并未选择物品，其价值为0

初始：dp[0][j]=0
递推规律：
$$dp[i+1][j]=\{\begin{array}{ll}dp[i][j]& \text{当a[i]>j}\\ max(dp[i][j],dp[i][j-a[i]]+b[j])& \text{其他}\end{array}$$
同样可的到一个dp二维数组

3.基于一维数组的动态规划
这部分还不太懂.………类似于Dijkstra算法。