并查集与食物链

并查集

1.并查集的基本操作

是用来管理分组情况的数据结构。
可以进行以下操作

• 并查集初始化
• 查询两元素是否在同一组
• 合并两元素所在的组（并查集没有拆开的操作）

举个栗子：

注：

• 并查集是利用树的结构来实现的，不过并非二叉树，也可能是三叉树、四叉树……
• 并查集的时间复杂度为阿克曼函数（Ackermann）的反函数，比O(logn)还快

1.初始化

• 设置一维数组p[]用于判断他们的分组
  

void init(int n) {
	for (int i = 0; i < n; i++) {
		par[i] = i;
		rank[i] = 0;
	}
}

2.查询

• 如下图：p[2]=5，p[9]=5，而p[5]=5 ，这一组的组名就是5。
• 在查询两个元素是否为同一组时，需要先求出他们的root也就是这里的5

int find(int x) {
	int r = x;
	while (r != par[r]) {
		r = par[r];
	}
	return r;
}
bool same(int x, int y) {
	if (find(x) == find(y)) return true;
	else return false;
}

3.合并

void unit(int x, int y) {
	x = find(x);
	y = find(y);
	if (x == y) return;
    //依据树高对树的优化
	if (rank[x] < rank[y]) par[x] = y;
	else if (rank[x] > rank[y]) par[y] = x;
	else if (rank[x] == rank[y]) {
		par[y] = x;
		rank[x]++;
	}
}

2.优化

1.注意树的高度

• 在树形结构中经常发生退化现象
• 因此我们设置rank数组来记录树的高度，以防止出现退化现象

对应有两种情况：

1.rank[6]==rank[7]

2.rank[6]>rank[7]

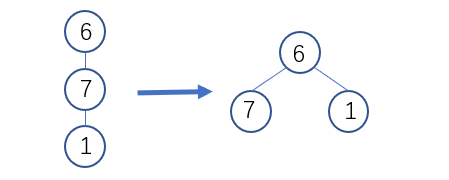
2.路径的压缩

• 如图所示方法可缩短搜索的时间
  

---

食物链

有N只动物，分别编号为1,2,3……N。所有动物都属于A,B,C中的其中一种。已知A吃B、B吃C、C吃A。按顺序给出下面两种信息共K条。

• 第一种：x与y属于同一种类
• 第二种：x吃y

然而这些信息优势会出错。有可能有的信息和之前给的信息矛盾，也有的信息可能给出的x与y不在1,2……N的范围内。求在K条信息中有多少条是不正确的。计算过程中，我们忽视此类的错误信息。

Sample Input:
N=100,K=7
信息有K条：
第一种，x=101，y=1
第二种，x=1，y=2
…… ……

首先确定此题的分类用到并查集
难点：每种动物都有三种类别，如何处理这三种类别和两种关系

那么我们设置一个3*N的一维数组（二维数组也可）

如图：

• 1与2属于第一种关系，那么将对应连线部分并入同一类
• 3与4属于第二种关系，将对应部分并入同类

• 相反如图所示两种情况，那么说明有信息错误

#include"stdio.h"
#include"stdlib.h"
#define MAX 100

//并查集所需数组
int par[MAX], rank[MAX];
int N, K;
//t数组是信息类别，X存储每条信息中的x,Y存储每条信息的y
int t[MAX], X[MAX], Y[MAX];

//并查集相关操作
void init(int n) {
	for (int i = 0; i < n; i++) {
		par[i] = i;
		rank[i] = 0;
	}
}

int find(int x) {
	int r = x;
	while (r != par[r]) {
		r = par[r];
	}
	return r;
}

void unit(int x, int y) {
	x = find(x);
	y = find(y);
	if (x == y) return;

	if (rank[x] < rank[y]) par[x] = y;
	else if (rank[x] > rank[y]) par[y] = x;
	else if (rank[x] == rank[y]) {
		par[y] = x;
		rank[x]++;
	}
}

bool same(int x, int y) {
	if (find(x) == find(y)) return true;
	else return false;
}

void solve() {
	int ans = 0;
	init(3 * N);
	//检测每一条信息
	for (int i = 0; i < K; i++) {
		int x = X[i] - 1;
		int y = Y[i] - 1;
		//第一种信息
		if (t[i] == 1) {
			//当x与y有第二种关系，信息错误
			if (same(x, y + N) || same(x, y + 2 * N))
				ans++;
			//两者无关事，合并对A,B,C三种同时合并
			else {
				unit(x, y);
				unit(x + N, y + N);
				unit(x + 2 * N, y + 2 * N);
			}
		}
		//第二种信息
		if (t[i] == 2) {
			if (same(x, y + N) || same(x, y + 2 * N))
				ans++;
			else {
				unit(x, y + N);
				unit(x + N, y + 2 * N);
				unit(x + 2 * N, y);
			}
		}
	}
	printf("%d\n", ans);
}

int main() {
	scanf_s("%d%d", &N, &K);
	for (int i = 0; i < K; i++) {
		scanf_s("%d", &t[i]);
		scanf_s("%d", &X[i]);
		scanf_s("%d", &Y[i]);
	}
	solve();
	system("pause");
}