假设存在两种对象,它们之间存在某种联系,并且它们各自存在某种属性(称为潜在因素latent factor),我们希望通过现存的联系来分析出它们各自的属性,从而对它们的后继行为进行预测,这也是推荐系统常用的方法之一。
肥宅买公仔
以肥宅买公仔为例,假设每个公仔有傲娇的属性或天然呆的属性,而每个肥宅有偏爱傲娇的属性或偏爱天然呆的属性,那偏爱傲娇的肥宅会更多地购买具有傲娇属性的公仔,偏爱天然呆的肥宅会更多地购买具有天然呆属性的公仔。
但大多数情况下我们并不知道公仔和肥宅背后的属性是什么,只知道肥宅购买公仔的情况,于是我们希望通过肥宅购买各个公仔的数量分析出它们各自背后的属性。
matrix expression
现在以一个matrix的形式表示肥宅购买公仔的情况。
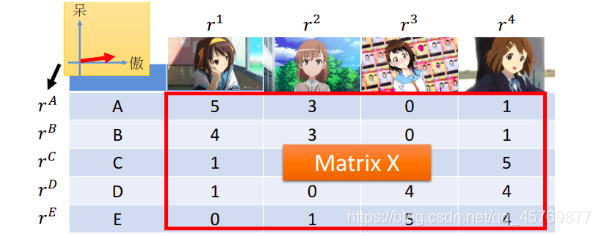
购买公仔数目看成matrix X X X,纵坐标代表肥宅 { r A \{r^A {rA、 r B r^B rB、 r C r^C rC、 r D r^D rD、 r E } r^E\} rE},而横坐标代表公仔 { r 1 \{r^1 {r1、 r 2 r^2 r2、 r 3 r^3 r3、 r 4 } r^4\} r4},其中每个肥宅个体和每个公仔个体都是用feature vetor来表示。matrix X X X里的每个element,都是由属于肥宅的feature vector和属于公仔的feature vector的内积得到。
M
=
[
r
A
r
B
r
C
r
D
r
E
]
[
r
1
r
2
r
3
r
4
]
\begin{aligned} &M= \left [ \begin{matrix} r^A\\ r^B\\ r^C\\ r^D\\ r^E \end{matrix} \right ] \left [ \begin{matrix} r^1\ r^2\ r^3\ r^4 \end{matrix} \right ] \end{aligned}
M=⎣⎢⎢⎢⎢⎡rArBrCrDrE⎦⎥⎥⎥⎥⎤[r1 r2 r3 r4]
M
=
[
r
1
A
r
2
A
.
.
.
r
k
A
r
1
B
r
2
B
.
.
.
r
k
B
r
1
C
r
2
C
.
.
.
r
k
C
r
1
D
r
2
D
.
.
.
r
k
D
r
1
E
r
2
E
.
.
.
r
k
E
]
[
r
1
1
r
1
2
r
1
3
r
1
4
r
2
1
r
2
2
r
2
3
r
2
4
⋮
⋮
⋮
⋮
r
k
1
r
k
2
r
k
3
r
k
4
]
\begin{aligned} &M= \left [ \begin{matrix} r^A_1\ r^A_2 ...r^A_k \\ r^B_1\ r^B_2 ...r^B_k \\ r^C_1\ r^C_2 ...r^C_k \\ r^D_1\ r^D_2 ...r^D_k \\ r^E_1\ r^E_2 ...r^E _k \end{matrix} \right ] \left [ \begin{matrix} r^1_1\ r^2_1\ r^3_1\ r^4_1\\ r^1_2\ r^2_2\ r^3_2\ r^4_2\\ \vdots\ \ \ \ \vdots\ \ \ \ \vdots\ \ \ \ \vdots\\ r^1_k\ r^2_k\ r^3_k\ r^4_k\\ \end{matrix} \right ] \end{aligned}
M=⎣⎢⎢⎢⎢⎡r1A r2A...rkAr1B r2B...rkBr1C r2C...rkCr1D r2D...rkDr1E r2E...rkE⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎡r11 r12 r13 r14r21 r22 r23 r24⋮ ⋮ ⋮ ⋮rk1 rk2 rk3 rk4⎦⎥⎥⎥⎤
- 5 × 4 m a t r i x = ( 5 × k m a t r i x ) × ( k × 4 m a t r i x ) 5×4\ matrix=(5×k\ matrix)\ ×\ (k×4\ matrix) 5×4 matrix=(5×k matrix) × (k×4 matrix)
- k k k 表示latent factor数量
solution
SVD
可以使用SVD来分解得到各自的feature vector。

latent factor的数量
K
K
K,需要自己去调整,我们要做的事寻找找一组
r
A
r^A
rA~
r
E
r^E
rE和
r
1
r^1
r1~
r
4
r^4
r4,使得右侧两个矩阵相乘的结果与左侧的matrix
X
X
X越接近越好,可以使用SVD的方法求解。
gradient descent
martix的部分值可能会丢失,在不填值的情况下SVD难以处理,我们可以使用梯度下降的方法求解。

loss function:
L
=
∑
(
i
,
j
)
(
r
i
⋅
r
j
−
m
i
j
)
2
L=\sum\limits_{(i,j)}(r^i\cdot r^j-m_{ij})^2
L=(i,j)∑(ri⋅rj−mij)2
r
i
r^i
ri指肥宅的latent factor,
r
j
r^j
rj指公仔的latent factor,
m
i
j
m_{ij}
mij是Matrix
x
x
x上的未缺失值,对所有的
r
i
r^i
ri和
r
j
r^j
rj进行梯度下降,上式计算的好处是可以跳过缺失数据。
prediction
假设latent factor的数目等于2,则人的属性 r i r^i ri和动漫角色的属性 r j r^j rj都是2维的vector,在进行Matrix Factorization之后得到肥宅和公仔各自的latent factor,并利用latent factor可以预测缺失值。
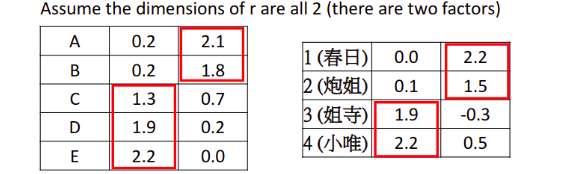 latent factor latent factor
|
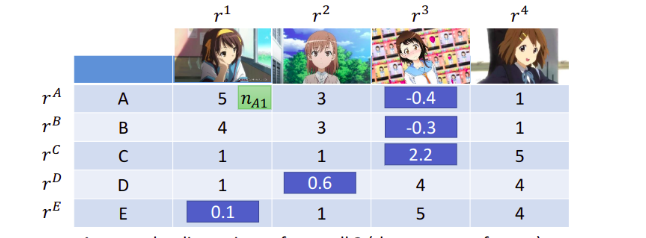 缺失值预测 缺失值预测
|
这里实际进行计算后,把属性中较大值标注出来,可以发现:
- 公仔:1、2有相似属性,3、4属于有相似属性
- 肥宅:A、B有相似偏好,C、D、E有相似偏好
结合动漫角色,可以分析出动漫角色的第一个维度是天然呆属性,第二个维度是傲娇属性,接下来通过向量乘法即可预测得到matrix x x x在相应位置的缺失值,这也是推荐系统的常用方法。
other fectors
实际上除了肥宅和公仔自身的属性外,可能还存在其他因素影响购买,因此我们可以将式子更精确地改写为:
m
i
j
≈
r
i
⋅
r
j
+
b
i
+
b
j
m_{ij}≈r^i\cdot r^j+b_i+b_j
mij≈ri⋅rj+bi+bj
loss function:
L
=
∑
(
i
,
j
)
(
r
i
⋅
r
j
+
b
i
+
b
j
−
n
i
j
)
2
L=\sum\limits_{(i,j)}(r^i\cdot r^j+b_i+b_j-n_{ij})^2
L=(i,j)∑(ri⋅rj+bi+bj−nij)2
- b i b_i bi表示肥宅 i i i对买公仔的热爱程度
- b j b_j bj表示公仔 j j j的限量程度
还可以添加其他与这些latent vector无关的item,同时还可以加上一些regularization去对结果做约束。
Topic Analysis
matrix factorization用在topic analysis上的方法,叫做LSA(Latent semantic analysis),潜在语义分析。我们需要把公仔换成文章,人换成词汇,表中的值从购买数量换成词频即可,我们可以用词汇的重要性给词频加权,在各种文章中出现次数越多的词汇越不重要,出现次数越少则越重要。
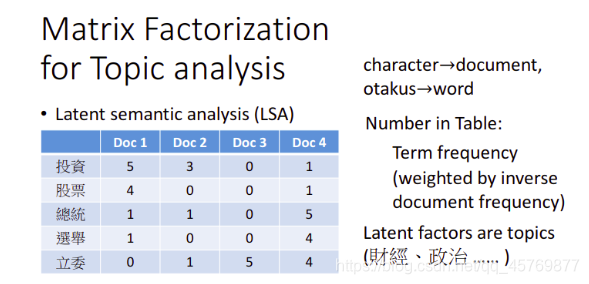
这个场景下找出的latent factor可能会是主题(topic),比如某个词汇或某个文档有多少比例是偏向于财经主题、政治主题。





















 546
546

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








