冗余路径
题目描述

核心思路
从题目描述中的“每一对草场之间都会至少有两条相互分离的路径”和“两条路径相互分离,是指两条路径没有一条重合的道路”,可以知道这其实就是边双连通图的定义。
在同一个边双连通分量中,任意两点都有至少两条独立路径可达,所以同一个边双连通分量里的所有点可以看做同一个点,于是可以把一个边双连通分量进行“缩点”。把所有的边双连通分量都进行缩点后,那么就会形成一棵树。树中的节点就是边双连通分量缩完之后的点,而树中的边其实就是割边。
题目是说要新建一些道路,使得它成为边双连通图。那么转化为:在树中至少添加多少条边能使图变为边双连通图
这里有一个定理:统计出树中度为1的结点的个数,即叶结点的个数,记为 leaf ,则要使树中任意两个节点之间都有两条独立的路径,则需要添加的边数为 ⌊ l e a f + 1 2 ⌋ \lfloor \dfrac {leaf+1}{2}\rfloor ⌊2leaf+1⌋
证明还不会,但是可以用下面的栗子来解释一下:
当叶子节点的个数 l e a f leaf leaf为偶数时:
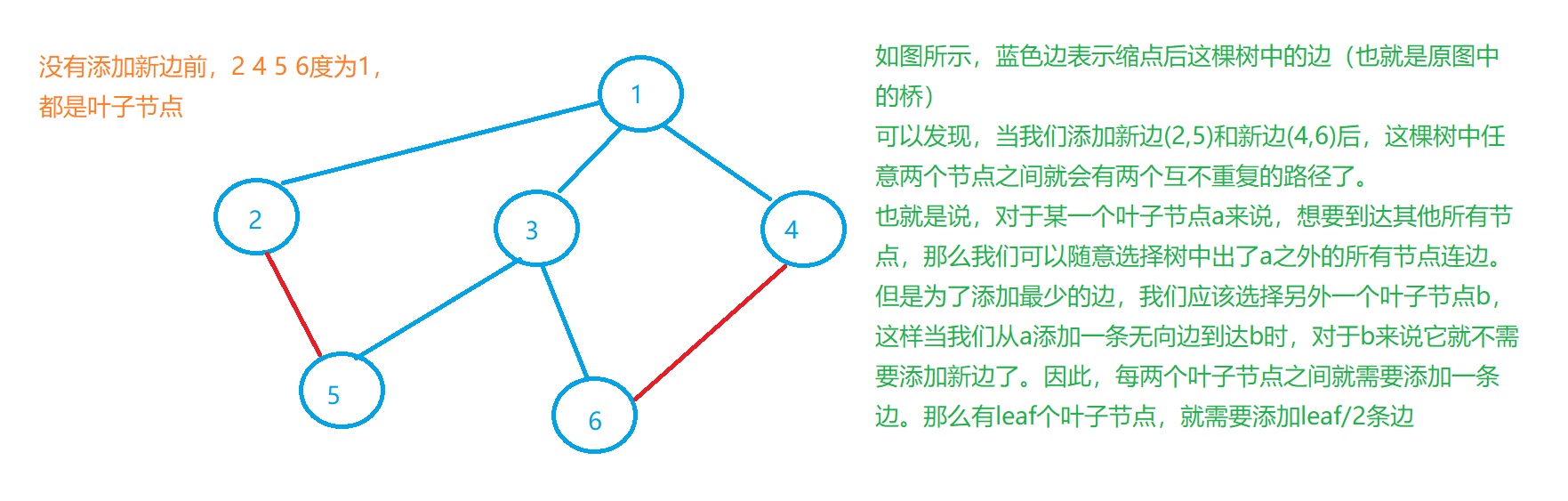
当叶子节点的个数 l e a f leaf leaf为奇数时:
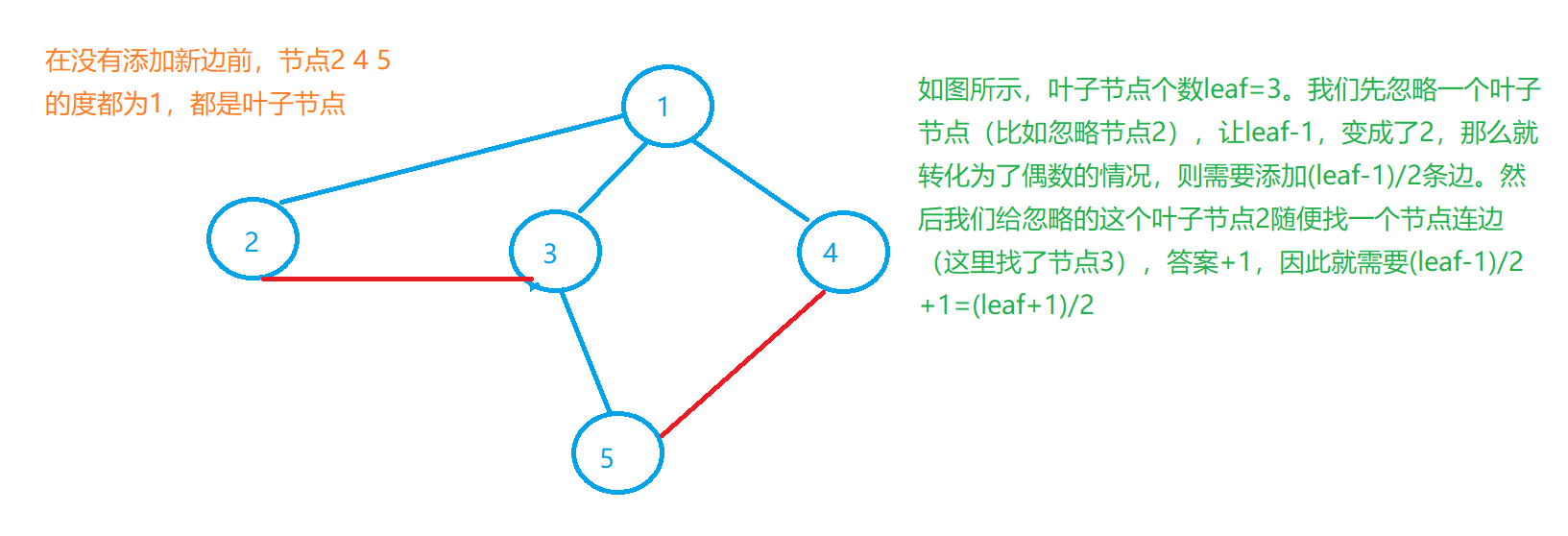
综上,结合 l e a f 2 \dfrac {leaf}{2} 2leaf和 l e a f + 1 2 \dfrac {leaf+1}{2} 2leaf+1答案就是 l e a f + 1 2 \dfrac {leaf+1}{2} 2leaf+1向下取整
算法设计:
- 先把原图建立出来
- tarjan求割边,同时求出边连通分量,缩点
- 遍历每一条边,找到割边,设这条割边的两个端点为 x , y x,y x,y,节点 x x x所在的边连通分量为 a = i d [ x ] a=id[x] a=id[x],节点 y y y所在的边连通分量为 b = i d [ y ] b=id[y] b=id[y],分别统计 a , b a,b a,b的度
- 遍历这
e_dcc个边连通分量,其实也就是缩完之后的e_dcc个点,统计入度为1的顶点个数,最终答案就是 l e a f + 1 2 \dfrac {leaf+1}{2} 2leaf+1向下取整
代码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=5010,M=20010;
int n,m;
int h[N],e[M],ne[M],idx;
int dfn[N],low[N],num;
int stk[N],top;
int id[N],e_dcc; //e_dcc是边连通分量的个数
int d[N]; //统计缩完点之后这棵树中每个顶点(边连通分量)的度
//bridge[i]=bridge[i^1]=true表示节点e[i]与节点e[i^1]之间的这条边是桥
bool bridge[M];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
//由于无向图中,从子节点到父节点的这条边是不需要处理的 因此需要记录子节点是父节点从边from走过来的
//目的是为了防止子节点又通过from这条边走回到父节点 这样就不能判定割边了
//from表示 当前节点y是上一个节点x通过边from到达的
void tarjan(int x,int from)
{
dfn[x]=low[x]=++num;
stk[++top]=x;
//遍历节点x的所有邻接点
for(int i=h[x];~i;i=ne[i])
{
int y=e[i]; //y是i的邻接点
//如果节点y还没有被访问过
if(!dfn[y])
{
tarjan(y,i); //递归访问y
low[x]=min(low[x],low[y]); //回溯时更新
//满足割边判定法则
if(low[y]>dfn[x])
bridge[i]=bridge[i^1]=true; //表示节点e[i]与节点e[i^1]之间的这条边是桥
}
//否则说明节点y已经被访问过了 但是有可能节点y可以通过非树边(非父子边)追溯到更早的节点
//那么也是可以更新的 一条无向边可以看作是两条反向的有向边
//x通过from这条边到达y,即x->y是通过from边,那么y就可以通过from^1这条边到达x,即y->x是通过from^1边
//为了防止从子节点y走回到了父节点x 那么此时y就不能走from^1这条边
else if(i!=(from^1))
low[x]=min(low[x],dfn[y]);
}
//记录节点分别属于哪些边连通分量
if(dfn[x]==low[x])
{
e_dcc++;
int y;
do{
y=stk[top--];
id[y]=e_dcc;
}while(y!=x);
}
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
while(m--) //建立原图
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b),add(b,a);
}
tarjan(1,-1); //tarjan求桥 然后求边连通分量 缩点
//遍历每一条边,找到割边,给这条割点的两个端点所在的边连通分量的度+1
//注意这里是统计每个点的度,成对变换时是(0,1) (2,3) (4,5)
//节点0的这个边连通分量的度要+1 同时节点1的这个边连通分量的度也要+1 否则就会出错
//因为无向边就是两条反向的有向边 因此如果写成i+=2的话 那么其实就只枚举了这个无向边中的正向边
//那么只会使得一个点的度+1 而另一个点的度不会+1
for(int i=0;i<idx;i++) //总共有idx条边
{
if(bridge[i])//如果i这条边是桥
{
int j=e[i]; //记录这条割边的一个端点j
int a=id[j]; //记录这个端点j所在的边连通分量的编号a
d[a]++; //缩点后的节点a的度+1
}
}
int leaf=0; //树中节点度为1的个数
//统计树中节点度为1的节点个数
for(int i=1;i<=e_dcc;i++)
if(d[i]==1)
leaf++;
printf("%d\n",(leaf+1)/2); //答案
return 0;
}
























 245
245











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










