区间DP.

琛_

已于 2022-02-03 18:35:33 修改

阅读量1.1k

点赞数

分类专栏： AcWing算法提高课文章标签：算法动态规划

于 2022-01-30 20:39:02 首次发布

本文链接：https://blog.csdn.net/qq_45896050/article/details/122753688

版权

AcWing算法提高课专栏收录该内容

18 篇文章 1 订阅

订阅专栏

区间DP

环形石子合并
能量项链
加分二叉树
凸多边形的划分
棋盘分割

环形石子合并

将 n 堆石子绕圆形操场排放，现要将石子有序地合并成一堆。

规定每次只能选相邻的两堆合并成新的一堆，并将新的一堆的石子数记做该次合并的得分。

请编写一个程序，读入堆数 n 及每堆的石子数，并进行如下计算：

选择一种合并石子的方案，使得做 n−1 次合并得分总和最大。
选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。

输入格式
第一行包含整数 n，表示共有 n 堆石子。

第二行包含 n 个整数，分别表示每堆石子的数量。

输出格式
输出共两行：

第一行为合并得分总和最小值，

第二行为合并得分总和最大值。

数据范围
1 ≤ n ≤ 200

输入样例：

4
4 5 9 4

输出样例：

43
54

在这里插入图片描述
分析
拓展：

如果每轮合并的石子可以是任意的两堆石子，那么用到的就是经典的 Huffman Tree 的二叉堆模型
如果每轮合并的石子可以是任意的 nn 堆石子，那么用到的就是经典的 Huffman Tree 的 nn 叉堆模型
以上两种题型可以参考：

二叉堆：AcWing 148. 合并果子
nn 叉堆：AcWing 149. 荷马史诗

回归本题，本题要求每轮合并的石子 必须是相邻的 两堆石子，因此不能采用 Huffman Tree 的模型

这类限制只能合并相邻两堆石子的模型，用到的是经典的 区间DP 模型

考虑如何设定 动态规划 的阶段，既可以表示出初始每个石子的费用，也可以表示出合并后整个堆的费用

不妨把当前合并的石子堆的大小作为DP的阶段

这样 len=1 表示初值，即每个堆只有一个石子； len=n 表示终值，即一个堆中有所有的石子

这种阶段设置方法保证了我们每次合并两个区间时，他们的所有子区间的合并费用都已经被计算出来了

阶段设定好后，考虑如何记录当前的状态，无外乎就两个参数：

石子堆的左端点 l
石子堆的右端点 r

在区间DP中，我们也常常省去 lenlen 这一维的空间
因为 r−l+1=lenr−l+1=len，也就保证了在已知 ll 和 rr 的情况下，不会出现状态定义重复的情况
根据线性代数中方程的解的基本概念，我们就可以删掉 lenlen 这一维不存在的约束
但为了方便读者理解，以及介绍区间DP的阶段是如何划分的，我还是写了出来

以上就是所有有关石子合并的区间DP分析

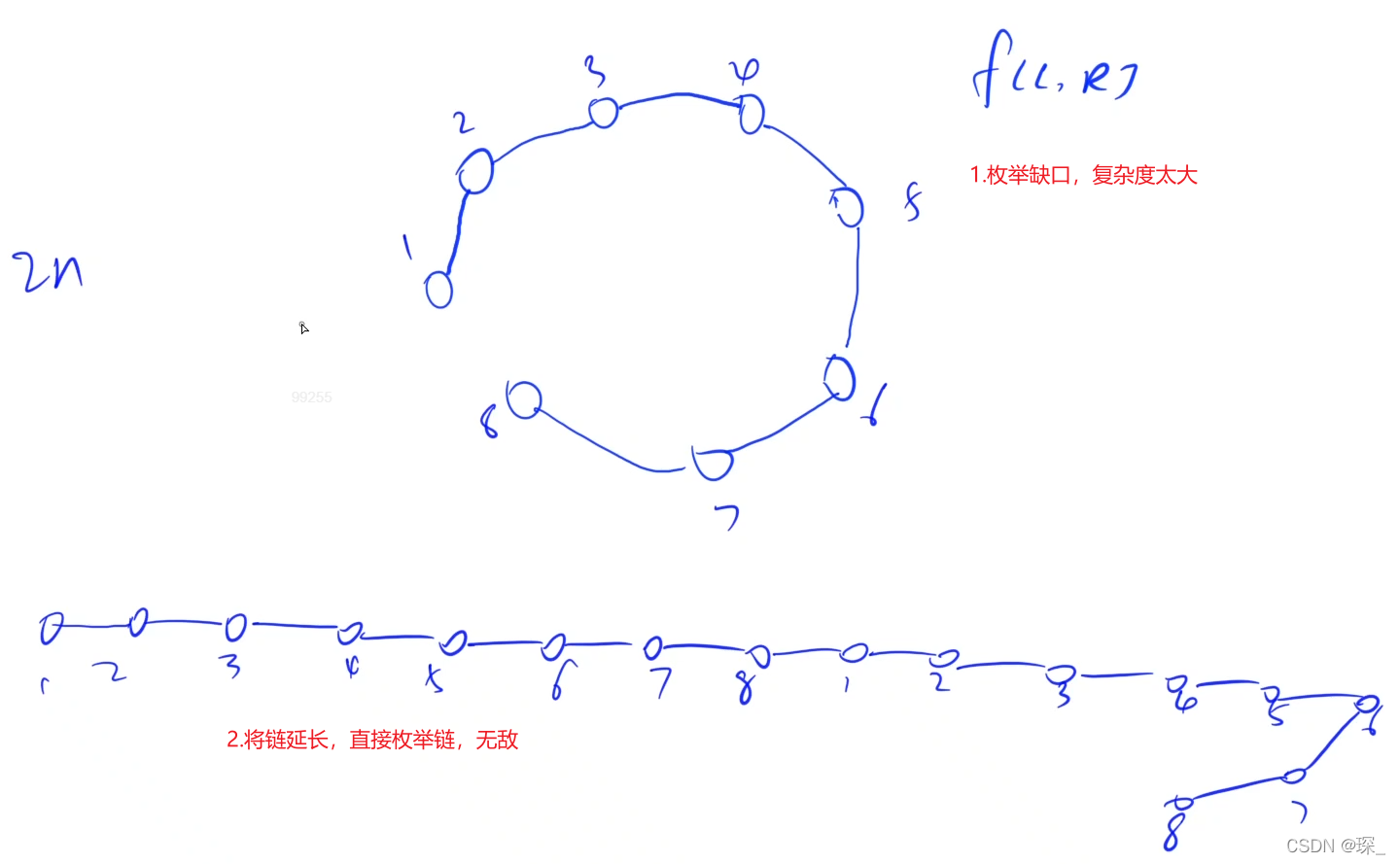
在考虑一下本题的 环形相邻 情况如何解决，方案有如下两种：

我们可以枚举环中分开的位置，将环还原成链，这样就需要枚举 n 次，时间复杂度为 O(n⁴)
我们可以把链延长两倍，变成 2n 个堆，其中 i 和 i+n 是相同的两个堆，然后直接套区间DP 模板，但对于阶段 len 只枚举到 n，根据状态的定义，最终可以得到所求的方案，时间复杂度为 O(n³)

一般常用的都是第二种方法，我也只会演示第二种方法的写法，对第一种有兴趣的读者可以自行尝试

时间复杂度：O(n³)

#include <cstring>
#include <iostream>
using namespace std;
const int N = 410;
int n;
int a[N], s[N];
int mx[N][N]; // 从i到j合并的最大值
int mi[N][N]; // 从i到j合并的最小值
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ ) {
        cin >> a[i];
        a[i + n] = a[i];
    }
    // 前缀和
    for (int i = 1; i <= 2 * n; i ++ ) s[i] = s[i - 1] + a[i];
    // 初始化数组
    memset(mx, -0x3f, sizeof mx);
    memset(mi, 0x3f, sizeof mi);
    // DP 迭代式
    for (int len = 1; len <= n; len ++ ) // 区间长度
        for (int l = 1; l + len - 1 <= 2 * n; l ++ ) { // 左右端点
            int r = l + len - 1;
            if (l == r) mx[l][r] = mi[l][r] = 0; // 一堆不需要合并
            else {
                // 枚举中间点
                for (int k = l; k < r; k ++ ) {
                    mx[l][r] = max(mx[l][r], mx[l][k] + mx[k + 1][r] + s[r] - s[l - 1]);
                    mi[l][r] = min(mi[l][r], mi[l][k] + mi[k + 1][r] + s[r] - s[l - 1]);
                }
            }
        }
    // 求结果
    int minv = 0x3f3f3f3f, maxv = -0x3f3f3f3f;
    for (int i = 1; i <= n; i ++ ) {
        minv = min(minv, mi[i][i + n - 1]);
        maxv = max(maxv, mx[i][i + n - 1]);
    }
    cout << minv << endl << maxv;
    return 0; 
}

为什么枚举中间点（分开点）时，可以取到左端点，但是不可以取到右端点？
经大佬点拨，明白，k 的取值范围，取决于定义的递推公式。以上代码定义的 k 为左半区间的右端点作为中间点，故 k 的取值范围为 l <= k < r，这样左半、右半区间都可以有仅取一个点的情况，不重不漏实现对左右区间的分割。
也可以将 k 定义为右半区间的左端点，这样k的范围就不一样了。

蒟蒻再次感谢彩色铅笔大佬

笔记学习：
作者：彩色铅笔
链接：https://www.acwing.com/solution/content/59932/
来源：AcWing

能量项链

在 Mars 星球上，每个 Mars 人都随身佩带着一串能量项链，在项链上有 N 颗能量珠。

能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。

并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。

因为只有这样，通过吸盘（吸盘是 Mars 人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。

如果前一颗能量珠的头标记为 m，尾标记为 r，后一颗能量珠的头标记为 r，尾标记为 n，则聚合后释放的能量为 m × r × n（Mars 单位），新产生的珠子的头标记为 m，尾标记为 n。

需要时，Mars 人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。

显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。

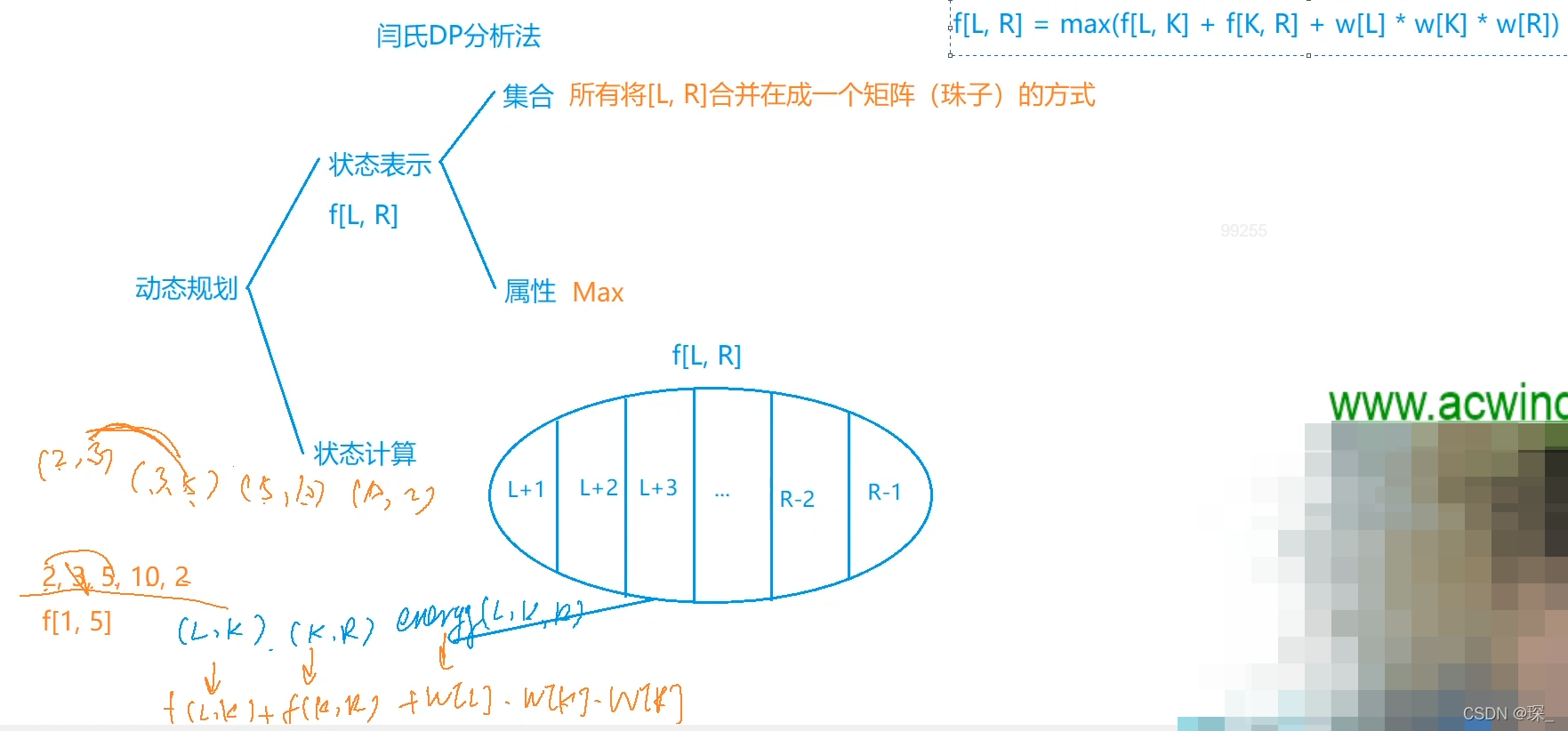
例如：设 N=4，4 颗珠子的头标记与尾标记依次为 (2，3)(3，5)(5，10)(10，2)。

我们用记号 ⊕ 表示两颗珠子的聚合操作，(j⊕k) 表示第 j，k 两颗珠子聚合后所释放的能量。则

第 4、1 两颗珠子聚合后释放的能量为：(4⊕1)=10×2×3=60。

这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。

输入格式
输入的第一行是一个正整数 N，表示项链上珠子的个数。

第二行是 N 个用空格隔开的正整数，所有的数均不超过 1000，第 i 个数为第 i 颗珠子的头标记，当 i<N 时，第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记，第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。

至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

输出格式
输出只有一行，是一个正整数 E，为一个最优聚合顺序所释放的总能量。

数据范围
4 ≤ N ≤ 100,
1 ≤ E ≤ 2.1×109

输入样例：

4
2 3 5 10

输出样例：

在这里插入图片描述

#include <iostream>
using namespace std;
const int N = 210;
int n, a[N];
int f[N][N];
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ ) {
        cin >> a[i];
        a[i + n] = a[i];
    }
    for (int len = 3; len <= n + 1; len ++ ) // 珠子的开头(2,3)结尾(10,2) 比输入的n多一个
        for (int l = 1; l + len - 1 <= n * 2; l ++ ) {
            int r = l + len - 1;
            for (int k = l + 1; k < r; k ++ )
                f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r] + a[l] * a[k] * a[r]);
        }
    int maxv = -0x3f3f3f3f;
    for (int i = 1; i <= n; i ++ )
        maxv = max(maxv, f[i][i + n]); // 右端点不减1是因为多一个
    cout << maxv;
    return 0;
}

加分二叉树

设一个 n 个节点的二叉树 tree 的中序遍历为（1,2,3,…,n），其中数字 1,2,3,…,n 为节点编号。

每个节点都有一个分数（均为正整数），记第 i 个节点的分数为 d_i，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：

subtree的左子树的加分 × subtree的右子树的加分＋ subtree的根的分数

若某个子树为空，规定其加分为 1。

叶子的加分就是叶节点本身的分数，不考虑它的空子树。

试求一棵符合中序遍历为（1,2,3,…,n）且加分最高的二叉树 tree。

要求输出：

（1）tree的最高加分

（2）tree的前序遍历

输入格式
第 1 行：一个整数 n，为节点个数。

第 2 行：n 个用空格隔开的整数，为每个节点的分数（0<分数<100）。

输出格式
第 1 行：一个整数，为最高加分（结果不会超过int范围）。

第 2 行：n 个用空格隔开的整数，为该树的前序遍历。如果存在多种方案，则输出字典序最小的方案。

数据范围
n < 30

输入样例：

5
5 7 1 2 10

输出样例：

145
3 1 2 4 5

算法

(区间DP,二叉树的遍历) O(n³)

状态表示： f[i][j] 表示中序遍历是 w[i ~ j] 的所有二叉树的得分的最大值。

状态计算： f[i][j] = max(f[i][k - 1] * f[k + 1][j] + w[k])，即将f[i][j]表示的二叉树集合按根节点分类，则根节点在 k 时的最大得分即为 f[i][k - 1] * f[k + 1][j] + w[k]，则f[i][j]即为遍历 k 所取到的最大值。

在计算每个状态的过程中，记录每个区间的最大值所对应的根节点编号。

那么最后就可以通过DFS求出最大加分二叉树的前序遍历了。

时间复杂度
状态总数是 O(n²)，计算每个状态需要 O(n) 的计算量，因此总时间复杂度是 O(n³)。

#include <iostream>
using namespace std;
const int N = 30;
int n;
int w[N];
int f[N][N]; // i到j形成的加分二叉树的最大值
int g[N][N]; // i到j形成的加分二叉树的根节点
void dfs(int l, int r) 
{
    if (l > r) return;
    int k = g[l][r];
    cout << k << ' ';
    dfs(l, k - 1);
    dfs(k + 1, r);
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> w[i];
    for (int len = 1; len <= n; len ++ )
        for (int l = 1; l + len - 1 <= n; l ++ ) {
            int r = l + len - 1;
            if (len == 1) f[l][r] = w[l], g[l][r] = l;
            else {
                for (int k = l; k <= r; k ++ ) {
                    int left = k == l ? 1 : f[l][k - 1];
                    int right = k == r ? 1 : f[k + 1][r];
                    int score = left * right + w[k];
                    if (f[l][r] < score) {
                        f[l][r] = score;
                        g[l][r] = k;
                    }
                }
            }
        }
    cout << f[1][n] << endl;
    dfs(1, n);
    return 0;
}

笔记、代码学习：
作者：yxc
链接：https://www.acwing.com/solution/content/3804/
来源：AcWing

凸多边形的划分

给定一个具有 N 个顶点的凸多边形，将顶点从 1 至 N 标号，每个顶点的权值都是一个正整数。

将这个凸多边形划分成 N−2 个互不相交的三角形，对于每个三角形，其三个顶点的权值相乘都可得到一个权值乘积，试求所有三角形的顶点权值乘积之和至少为多少。

输入格式
第一行包含整数 N，表示顶点数量。

第二行包含 N 个整数，依次为顶点 1 至顶点 N 的权值。

输出格式
输出仅一行，为所有三角形的顶点权值乘积之和的最小值。

数据范围
N ≤ 50,
数据保证所有顶点的权值都小于10⁹

输入样例：

5
121 122 123 245 231

输出样例：

12214884

回归本题，本题是一个给定的 凸多边形 求 三角剖分 的最小费用方案

很显然一个 凸多边形的剖分方案 并不唯一：

在选定多边形中 两个点 后，找出 三角形 的 第三个点 的方案有 n−2 个
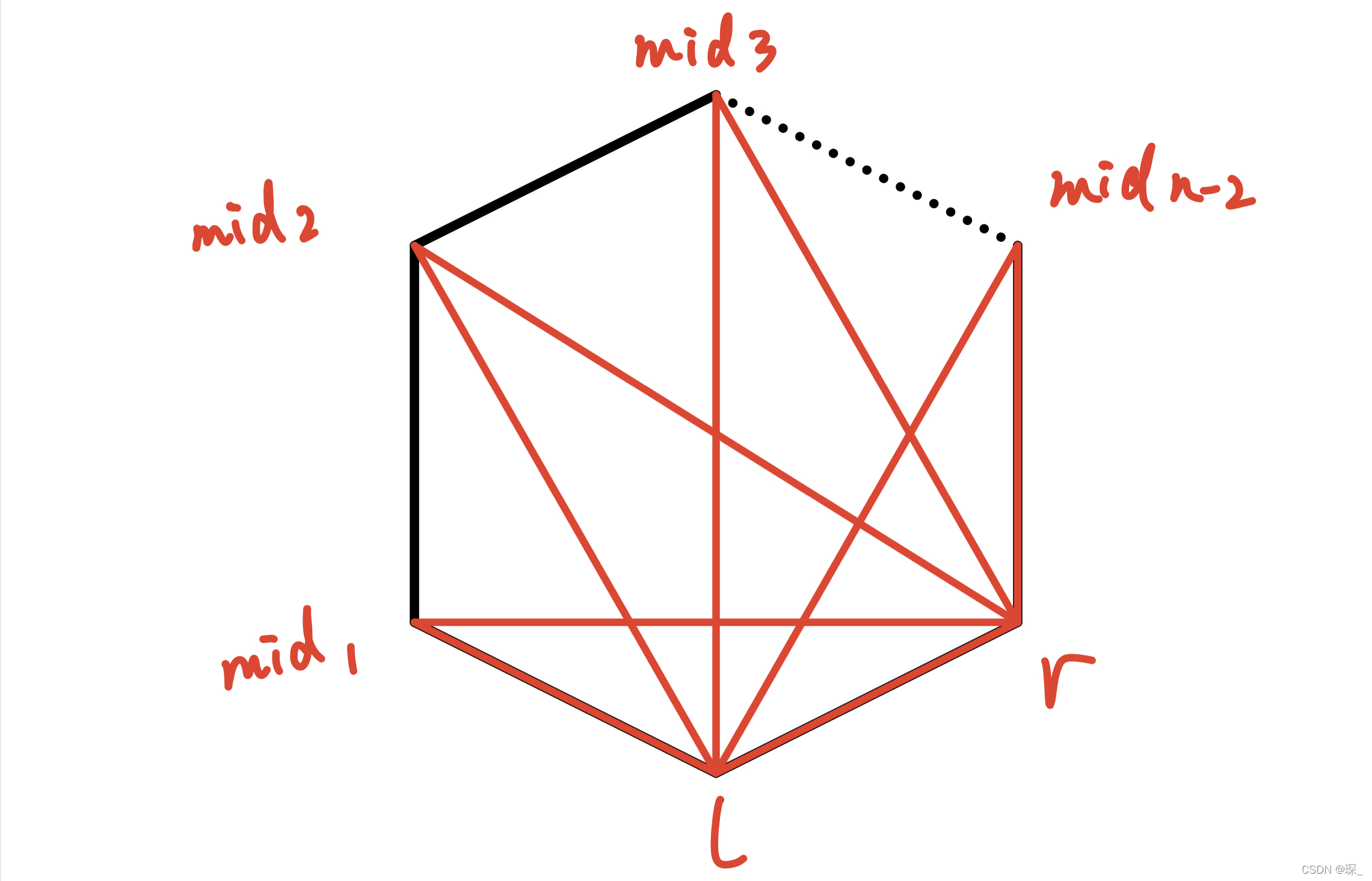
在这里插入图片描述
然后还要分别划分他的 左右两块区域

因此我们就会想到用 记忆化搜索 或者 区间DP 来进行处理

记忆化搜索介绍可以参考这篇加分二叉树【记忆化搜索思想】

区间DP介绍可以参考这篇环形石子合并【区间DP+环形区间问题】

本题解采用区间DP 的方式进行求解

在这里插入图片描述
区间DP 在状态计算的时候一定要认真划分好边界和转移，对于不同题目是不一样的

然后本题非常的嚣张，直接用样例的 5 的点告诉我们答案会爆 int 和 longlong
并且没有取模要求，那就只能上 高精度 了

时间复杂度： O(n³) 区间DP

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL; 
const int N = 55;
int n;
int w[N];
vector<int> f[N][N]; // 左端点i 右端点j 的权值乘积之和的最小值 
bool cmp(vector<int> &a, vector<int> &b)
{
	if (a.size() != b.size()) return a.size() < b.size();
	for (int i = a.size() - 1; i >= 0; i -- ) 
		if (a[i] != b[i])
			return a[i] < b[i];
	return true;
}
vector<int> add(vector<int> a, vector<int> b)
{
	vector<int> c;
	int t = 0;
	for (int i = 0; i < a.size() || i < b.size(); i ++ ) {
		if (i < a.size()) t += a[i];
		if (i < b.size()) t += b[i];
		c.push_back(t % 10);
		t /= 10;
	}
	while (t) c.push_back(t % 10), t /= 10;
	return c;
}
vector<int> mul(vector<int> a, LL b)
{
	vector<int> c;
	LL t = 0;
	for (int i = 0; i < a.size(); i ++ ) {
		t += b * a[i];
		c.push_back(t % 10);
		t /= 10;
	}
	while (t) c.push_back(t % 10), t /= 10;
	return c;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++ ) cin >> w[i];
	// 区间DP
	for (int len = 3; len <= n; len ++ ) 
		for (int l = 1; l + len - 1 <= n; l ++ ) {
			int r = l + len - 1;
			for (int k = l + 1; k < r; k ++ ) { // 中间点 
				auto new_val = mul(mul({w[l]}, w[k]), w[r]);
				new_val = add(add(new_val, f[l][k]), f[k][r]);
				if (f[l][r].empty() || cmp(new_val, f[l][r])) f[l][r] = new_val;
			}
		}
	auto res = f[1][n];
	for (int i = res.size() - 1; i >= 0; i -- ) cout << res[i];
	puts("");
	return 0;
}

笔记、代码学习：
作者：彩色铅笔
链接：https://www.acwing.com/solution/content/62040/
来源：AcWing

棋盘分割

将一个 8×8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 (n−1) 次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
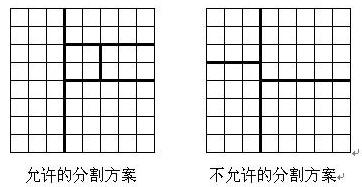
在这里插入图片描述
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。

现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并使各矩形棋盘总分的均方差最小。
在这里插入图片描述
请编程对给出的棋盘及 n，求出均方差的最小值。

输入格式
第 1 行为一个整数 n。

第 2 行至第 9 行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式
输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围
1 < n < 15

输入样例：

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例：

1.633

分析
本题如果用 动态规划 来分析，状态表示要至少开5维，记录分割操作的阶段，以及当前的棋盘状态

我这里直接贴出 闫氏DP分析法

闫氏DP分析法
状态表示 f_{k,x1,y1,x2,y2}—集合：

当前已经对棋盘进行了 k 次划分，且 k 次划分后选择的棋盘是左上角为 (x1,y1)，右下角为 (x2,y2)

状态表示 f_{k,x1,y1,x2,y2}—属性：

划分出来的 k+1 个子矩阵的 nσ²最小（下面给出了这样定义的原因）

状态计算 f_{k,x1,y1,x2,y2}：
在这里插入图片描述
这里关于 集合的属性 需要一点变化，直接使用 标准差 作为属性，在进行状态转移的时候不好计算

我们把标准差做出如下变化：
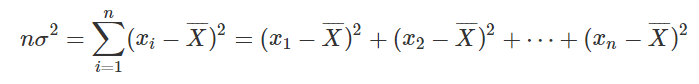
在这里插入图片描述
由于 σ 与 nσ² 的单调性相同，要求 σ 最小，就相当于 nσ² 最小

而转化为 nσ² 后，对于子状态，我们就可以直接进行 加法运算 来转移了（原来套着根号很难处理）

记忆化搜索
本题有这明显的分治引导，即给定一个初始的棋盘，然后我们选择进行分割

分割完后，选择保留一个棋盘，然后对另一个棋盘继续进行分割

直到分割次数达到上限 n−1
考虑一下直接递归操作的时间复杂度：
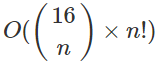
O((16n)×n!)
这是一个排列数，计算方法很简单，每轮会使用一条分割线，且每条分割线在一个方案里仅能使用一次

不难发现，递归操作会有很多冗余的重复计算，于是我们可以采用 记忆化搜索 进行优化

f_{k,x1,y1,x2,y2} 表示对棋盘进行了 k 次划分，且 k 次划分后选择的棋盘是左上角为 (x1,y1)，右下角为 (x2,y2)
这一步分析就有点雷同于上面的 DP 了

关于如何枚举矩阵的分割
由于我们这里记录矩阵的状态是通过他的 对角顶点 记录的，因此分割是我们也可以通过枚举对角顶点完成分割

如下图所示：

竖着切：
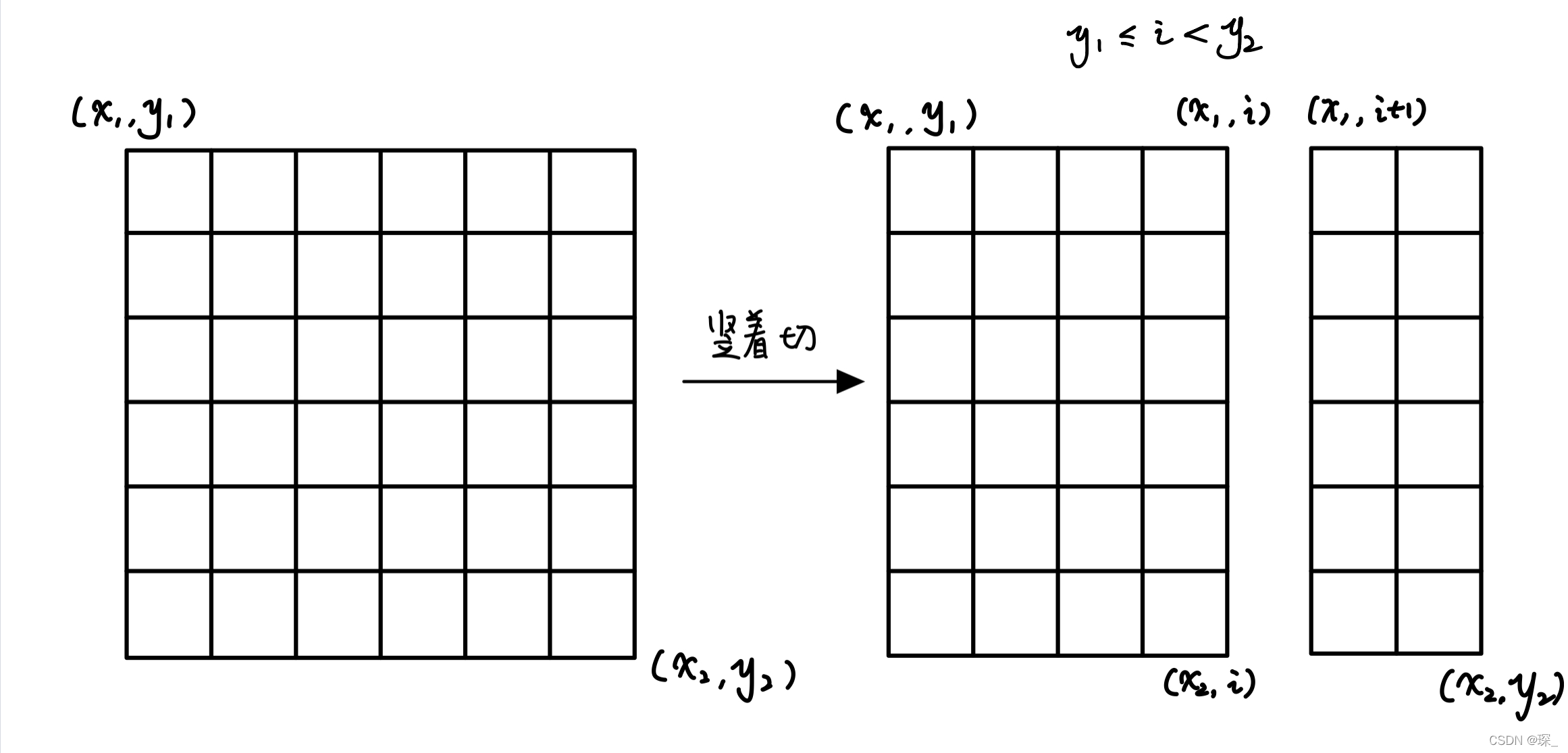
在这里插入图片描述
横着切：

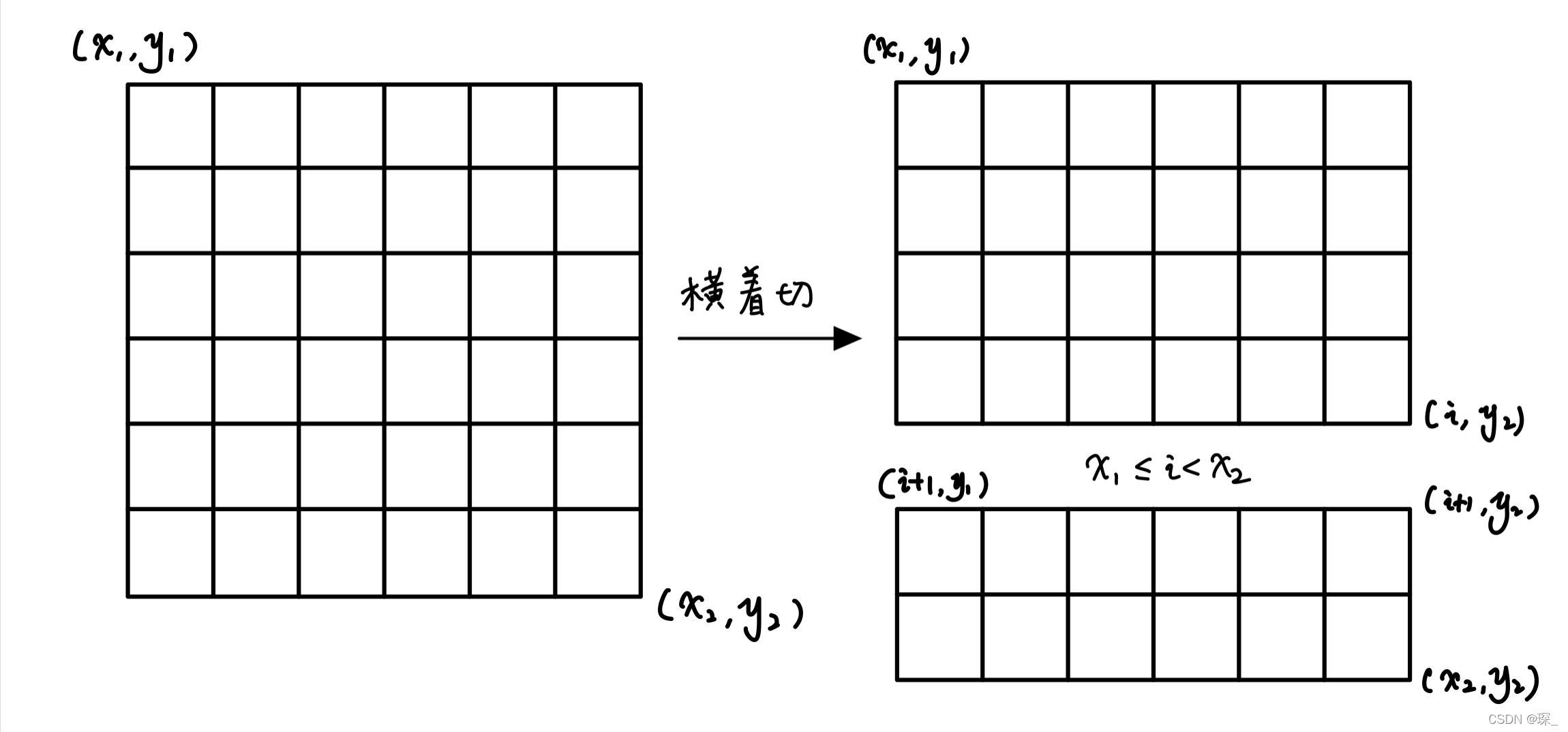
记忆化搜索
由于会频繁地计算某个矩阵的方差，因此我们需要先预处理出前缀和，保证计算方差的时间复杂度为 O(1)
时间复杂度：O(n⁵)

 #include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 15, M = 9;
const double INF = 1e9;
int n, m = 8;
int s[M][M];
double f[M][M][M][M][N]; // x1 y1 x2 y2 剩余需要的矩形数量k
double X;
int get_sum(int x1, int y1, int x2, int y2)
{
	return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}
double get(int x1, int y1, int x2, int y2)
{
	double sum = get_sum(x1, y1, x2, y2) - X;
	return (double)sum * sum / n;
}
double dp(int x1, int y1, int x2, int y2, int k)
{
	double &v = f[x1][y1][x2][y2][k];
	if (v >= 0) return v; // 切过了 
	if (k == 1) return v = get(x1, y1, x2, y2); // 不能切 
	v = INF;
	// 横切 
	for (int i = x1; i < x2; i ++ ) {
		v = min(v, get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1)); // 继续切割下半部份 
		v = min(v, get(i + 1, y1, x2, y2) + dp(x1, y1, i, y2, k - 1)); // 继续切割上半部份 
	}
	// 竖切
	for (int i = y1; i < y2; i ++ ) {
		v = min(v, get(x1, y1, x2, i) + dp(x1, i + 1, x2, y2, k - 1)); // 继续切割右半部份
		v = min(v, get(x1, i + 1, x2, y2) + dp(x1, y1, x2, i, k - 1)); // 继续切割左半部份 
	} 
	return v;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= m; i ++ )
		for (int j = 1; j <= m; j ++ ) {
			cin >> s[i][j];
			s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
		}
	X = (double) s[m][m] / n;
	memset(f, -1, sizeof f);
	printf("%.3lf\n", sqrt(dp(1, 1, 8, 8, n)));
	return 0;
}