梯度下降

1. 梯度下降法（gradient descent），又名最速下降法（steepest descent）是求解无约束最优化问题最常用的方法，它是一种迭代方法.1847年由著名的数学家柯西Cauchy给出如果函数为一元函数，梯度就是该函数的导数
   
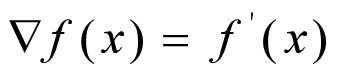
   二元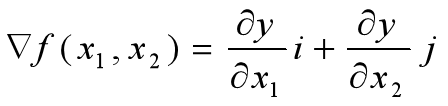2. 在梯度下降法中，求某函数极大值时，沿着梯度方向走，可以到达极大点；反之，沿着负梯度方向走，则最快地达到极小点。
   梯度下降法特点：越接近目标值，步长越小，下降速度越慢。
2. 相关概念
   梯度 : 表示某一函数在一点处变化率最快的方向向量(可理解为这点的导数/偏导数)
   样本 : 实际观测到的数据集，包括输入和输出(本文的样本数量用 m 表述,元素下标 i 表示)
   特征 : 样本的输入(本文的特征数量用 n 表示,元素下标 j 表示)
   假设函数 : 用来拟合样本的函数，记为 hθ(X) (θ 为参数向量, X 为特征向量)
   损失函数 : 用于评估模型拟合的程度，训练的目标是最小化损失函数，记为 J(θ)
   线性假设函数 :
   拟合函数：
   hθ(X)=θ0+θ1x1+θ2x2+⋯+θnxn=∑j=0nθjxj
   其中 X 为特征向量, θj为模型参数， xj 是特征向量的第 j 个元素(令x0=1)。
   向量形式：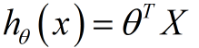
   经典的平方差损失函数如下：

J(θ)=1/2m∑i=1m(hθ(Xi)−yi)2
其中 m 为样本个数， Xi 为样本特征集合的第 i 个元素（是一个向量）， yi 是样本输出的第i个元素, hθ(Xi) 是假设函数。

注意：输入有多个特征时，一个样本特征是一个向量。假设函数的输入是一个特征向量而不是特征向量里面的一个元素
3. 梯度下降法-步骤
（1） 首先设定一个较小的正数，;
(2)2 求当前位置处的各个偏导数：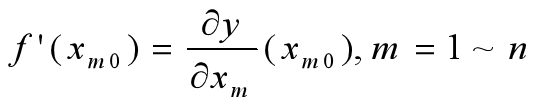
(3)修改当前函数的参数值，公式如下：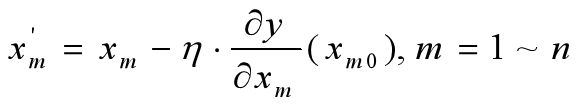
(4)如果参数变化量小于，退出；否则返回2。
4. 几种形式：
（1)批量梯度下降BGD（使用所有样本进行计算，慢但准确度好)
按照传统的思想，我们需要对上述风险函数中的每个求其偏导数，得到每个对应的梯度

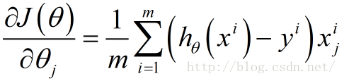
这里表示第i个样本点的第j分量，即h(θ)中的
接下来由于我们要最小化风险函数，故按照每个参数的负梯度方向来更新每一个

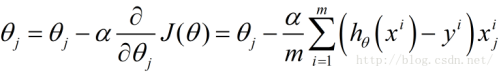
这里的α表示每一步的步长 （步长适中，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点)
(2)随机梯度下降SGD（样本多,但每次使用一个样本，准确度欠缺）

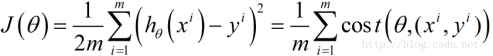
其中，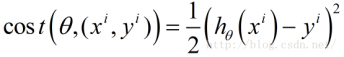
样本点的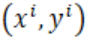损失函数
然后得到每个梯度，最后更新下一个梯度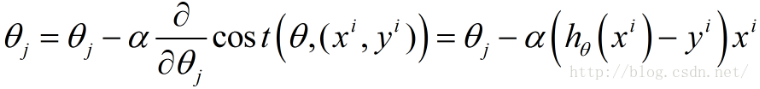
（3） 算法收敛判断方法
参数ΘT的变化距离为0，或者说变化距离小于某一阈值（ΘT中每个参数的变化绝对值都小于一个阈值）。为减少计算复杂度，该方法更为推荐使用。
J(Θ)不再变化，或者说变化程度小于某一阈值。计算复杂度较高，但是如果为了精确程度，那么该方法更为推荐使用。
（4)小批的梯度下降
这种方法把数据分为若干个批，按批来更新参数，这样，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不是很大。
5. 例子（借鉴)
这里用一个房屋价格评估的例子来使用梯度下降法。 我们知道房屋的价格跟很多因素相关（例如面积、房间书、地段等），每个因素都称之为特征(feature)。 这里假设房屋的面积是唯一特征（为简化模型而忽略其他的），已知的数据如下:

房屋面积: 45, 73, 89, 120, 140, 163 （平方米）

房屋价格: 80, 150, 198, 230, 280, 360 (万元）

根据这些数据可以使用下面的 python 代码做出面积和价格的三点图。

‘’‘
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

spaces = [45, 73, 89, 120, 140, 163]
prices = [80, 150, 198, 230, 280, 360]
spaces, prices = np.array(spaces), np.array(prices)
plt.scatter(spaces, prices, c=‘g’)
plt.xlabel(‘house space’)
plt.ylabel(‘house price’)
plt.show()

显示房屋面积和房屋价格的散点图

根据梯度下降法的步骤我们需要先给定假设函数 $h_{\theta }$ 和损失函数 $J(\theta )$，以及初始 $\theta$ 值。

这里房屋面积和价格的假设函数为： $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$ （一个特征）

损失函数使用平均方差函数: $J(\theta )=\frac{1}{2\ast 6}{\sum }_{i=1}^6(h_{\theta }(X_i)-y_i{)}^2$ （6个样本）

假设更新步长为 0.00005， 则更新公式为 $\theta_j = \theta_j - 0.00005 \cdot \dfrac{1}{6} \sum_{i=1}^6 (h_\theta(X_i) - y_i) \cdot X_{ij} $

其中 ${\theta }_j$ 包含 ${\theta }_0$ 和 ${\theta }_1$ ， $X_{i0}$ = 1。

注意: 如果步长选择不对，则 theta 参数更新结果会不对

使用下面 python 代码计算 $\theta$ 并画出 $h_{\theta }$ 函数 ：%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

theta 初始值

theta0 = 0
theta1 = 0

如果步长选择不对，则 theta 参数更新结果会不对

step = 0.00005

x_i0 = np.ones((len(spaces)))

假设函数

def h(x) :
return theta0 + theta1 * x

损失函数

def calc_error() :
return np.sum(np.power((h(spaces) - prices),2)) / 6

损失函数偏导数( theta 0)

def calc_delta0() :
return step * np.sum((h(spaces) - prices) * x_i0) / 6

损失函数偏导数( theta 1)

def calc_delta1() :
return step * np.sum((h(spaces) - prices) * spaces) / 6

循环更新 theta 值并计算误差，停止条件为

1. 误差小于某个值

2. 循环次数控制

k = 0
while True :
delta0 = calc_delta0()
delta1 = calc_delta1()
theta0 = theta0 - delta0
theta1 = theta1 - delta1
error = calc_error()

print(“delta [%f, %f], theta [%f, %f], error %f” % (delta0, delta1, theta0, theta1, error))

k = k + 1
if (k > 10 or error < 200) :
break

print(" h(x) = %f + %f * x" % (theta0, theta1))

使用假设函数计算出来的价格，用于画拟合曲线

y_out = h(spaces)

plt.scatter(spaces, prices, c=‘g’)
plt.plot(spaces, y_out, c=‘b’)
plt.xlabel(‘house space’)
plt.ylabel(‘house price’)
plt.show()

绿色的点是房屋面积和价格数据

蓝色的线是我们使用梯度下降法拟合出来的曲线

h(x) = 0.016206 + 2.078464 * x
png

通过运行上述代码，我们可以看出，梯度下降法的结果跟 $\theta$ 的初始值以及步长相关。 我们需要根据系统的特性凭经验给出 $\theta$ 和步长。

对于多特征系统来说，其实就是 $h_{\theta }$ 的改变而已，如果使用矩阵形式表示的话会更加方便。

假设函数向量形式（其中X是二维矩阵 m 行 n 列）：

损失函数向量形式（其中 Y 是 m 行 1 列的样本输出）：

$\theta$ 向量更新形式，令

我们改进一下上述 python 代码，使用矩阵处理以适应多特征系统并得出一样的结果。

注意: 用矩阵公式表示的时候没有除以样本数,实际写代码要除以样本数

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

输入数据格式:

1. 一个特征的是一维数组，表示样本

2. 多个特征的是二维数组，列表示特征数，行表示样本数

spaces = np.array([45, 73, 89, 120, 140, 163])
prices = np.array([80, 150, 198, 230, 280, 360])

步长

step = 0.00005

先计算输入的特征个数, 然后根据特征数生成 theta，并在样本数据前面插入一列全1数据

def genrate_model(inputs) :
_features = 2
_samples = inputs.shape[0]
if len(inputs.shape) == 2 :
_features = inputs.shape[2] + 1
_x0 = np.ones(_samples)
_theta = np.zeros(features)
return np.c[_x0, inputs], _theta, _samples

假设函数：输入数据矩阵与theta向量向乘, 返回多项式结果的一维矩阵

def h_a(x) :
return (theta * x).sum(axis=1)

损失函数

def e_a(x,y) :
return np.sum(np.power((h_a(x) - y),2)) / m

delta函数：计算偏导乘以补偿

def delta_a(x, y) :
return step * ((h_a(x) - y) * np.transpose(x)).sum(axis=1) / m

系统的特征数 + 1

x_data, theta, m = genrate_model(spaces)
y_data = prices

重新计算 delta 并更新 theta

k = 0
while True:
_d = delta_a(x_data, y_data)
theta = theta - _d
error = e_a(x_data, y_data)
# print(“delta”, _d, "theta ", theta , ", error ", error, "k ", k)
k = k + 1
if (k > 10 or error < 200) :
break;

打印 theta 结果，可以看出与上面 python 代码计算的结果是一致的。

print("theta array : " , theta)
theta array : [ 0.01620597 2.07846445]