目录
7.去除两类冗余的Bellman_Ford算法 == Dijkstra算法
(本文参考中国科学院大学卜东波老师课程内容,是算法课后代码实现复习的一份总结)
一:内容简介
单源最短路径问题是指计算从特定的源顶点到每一个顶点的最短路径,或则对称的,从每一个顶点到特定的目的顶点的最短路径;有向图中的最短路径和环有着密切的关系;故而我们定义环的权重为环里面边的权重加和,并依据权重将环分成正权重环,0权重环,负权重环;鉴于环对最短路径的重要性,我们依据是否存在环对图分类并设计相应的算法:(1)不存在环的有向图,称为有向无环图(DAG)(2)一般的有向图,对于一般的有向图来说,我们不仅需要在没有负权重环时能够计算最短路径,同时还需要判断是否存在负权重环。
针对上述的问题,本文会先对图的基本结构进行介绍,并对常用的广度搜索和深度搜索进行讲解,以及基于深度搜索的拓扑排序实现;而后我们针对有向无环图设计基于动态规划的算法;而后针对一般有向图,讲解经典的Bellman_ford算法,并对其运行规律进行分析,找出其存在的两类冗余情况,而后进行改善,设计出faster_bellman_ford算法;而后基于改进的faster_bellman_ford算法推出Dijkstra算法,并由此分析动态规划和贪心之间的联系与转换;上述讲述的所有算法皆基于python实现。

二:图的基础知识
1.图的基本结构与表示
图的基本要素包括顶点,边,权重,路径和环;对于图的实现,最简单的方式是邻接矩阵,在矩阵中,每一行和每一列都表示图中的一个顶点;而第i行和第j列交叉的格子中的值表示从顶点i到顶点j的边的权重,如果两个顶点被一条边连接起来,就称他们是相邻的;通过观察图表,我们可以看到该图较为的稀疏,而现实世界中大部分的图也是稀疏连接的,故而采取这种方式存储会浪费较多的空间,邻接矩阵的形式适用于具有较多边连接的图。

针对于稀疏图,更高效的方式是邻接表,在邻接表实现中,我们为图像中的所有顶点都保存一个主列表,同时为每一个顶点对象都维护一个列表,其中记录了与他相连的顶点;在具体的python实现中,我们使用字典,字典的键是连接的顶点,值是相应两个顶点之间边的权重。

邻接表的优点是其可以紧凑的表示稀疏图,此外,为了后续的方便,我们对于每一个顶点对象,不仅存储了以该节点为源节点的邻居节点,还可以存储以该节点为目的节点的邻居节点。在python中,我们通过字典来实现邻接表,为此,我们需要创建两个类;Graph类存储包含所有节点的主列表,Vertex类表示图中的每一个顶点。
2.图的具体实现Graph类和Vertex类
Vertex节点类其内容主要包括:
- 使用字典connectedto来记录以该节点为起点的节点以及权重。
- 使用字典connectedfrom来记录以该节点为终点的节点以及权重。
- 使用status来表示该节点的访问状态,'w'表示未访问,'g'表示正在访问,'b'表示访问结束,此主要用于深度搜索和广度搜索之中。
- 使用prefix表示该节点的前驱节点,其一般表示最短路径序列。
- 使用distance表示该节点从源节点其到此的最短距离。
- 使用方法addconnectedto和addconnectedfrom构建相应的边
- 使用方法getconnectedto和getconnectedfrom获取该节点的相应邻居节点
代码清单1-Vertex类
class Vector:
def __init__(self, key):
self.key = key
self.connectedto = {} # 记录以该节点为起点的节点以及权重
self.connectedfrom = {} # 记录以该节点为终点的节点以及权重
self.status = 'w'
self.prefix = None
self.start_time = 0
self.end_time = 0
self.distance = inf
def addconnectedto(self, keyto, weight):
self.connectedto[keyto] = weight
def addconnectedfrom(self, keyfrom, weight):
self.connectedfrom[keyfrom] = weight
def getconnectedto(self):
return self.connectedto.keys()
def getconnectedfrom(self):
return self.connectedfrom.keys()Graph图类其内容主要包括:
- Graph()新建一个空图,初始化主节点字典vertexlist 和节点数目vertexnum
- addVertex(key)向图中添加一个顶点实例
- addEdge(start, end, weight)向图中添加一条有向边,由节点start指向end
- dfs_visit(now_vertex, L)对节点now_vertex实现深度搜索
- topological_sort()对图进行拓扑排序
代码清单2-Graph 类
class Graph:
def __init__(self):
self.vertexlist = {}
self.vertexnum = 0
def addVertex(self, key):
self.vertexnum += 1
newvector = Vector(key)
self.vertexlist[key] = newvector
return newvector
def addEdge(self, start, end, weight):
if start not in self.vertexlist.keys():
self.addVertex(start)
if end not in self.vertexlist.keys():
self.addVertex(end)
self.vertexlist[start].addconnectedto(self.vertexlist[end], weight)
self.vertexlist[end].addconnectedfrom(self.vertexlist[start], weight)
接下来基于上述两类,我们将通过build_graph_dag将此前的有向无环图转换到代码世界中:
代码清单3-build_graph_dag
class shortest_path_graph:
def __init__(self):
return None
def build_graph_dag(self):
g = Graph()
Nodes = ['c', 'd', 't', 's', 'a', 'b']
for node in Nodes:
g.addVertex(node)
g.addEdge('s', 'a', 1)
g.addEdge('s', 'b', 1)
g.addEdge('a', 'b', 3)
g.addEdge('a', 'c', 4)
g.addEdge('a', 'd', 6)
g.addEdge('b', 'c', 5)
g.addEdge('b', 'd', 6)
g.addEdge('c', 'd', 7)
g.addEdge('c', 't', 8)
g.addEdge('d', 't', 9)
for v in g.vertexlist.values():
for w in v.connectedto:
print(v.key, w.key)
print('from')
for v in g.vertexlist.values():
for w in v.connectedfrom:
print(v.key, w.key)
return g三:有向无环图上的单源最短路径问题
1.问题阐述以及动态规划求解
继而我们可以讨论有向无环图上的单源最短路径问题:
输入:有向无环图G=<V,E>,边的权重w:E→R,源顶点s![]() ,其中V=n,E=m
,其中V=n,E=m
输出:s到每一个顶点v∈V的最短路径
由动态规划的思想以及最短路径的性质(最短路径中的子路径是其端点间的最短路径),我们可以把从源顶点 s 到目的顶点 t 的最短路径求解过程描述成一个多步决策过程:从 t 开始,每步确定最短路径中一条边。以第一步对 t 的决策为例,由于 t 有两个前驱顶点 b 和 d,因此我们需要在如下两个决策项中做最优选择:
(1) 从 b 到达 t:剩下的子问题是计算从 s 到 b 的最短路径;
(2) 从 d 到达 t:剩下的子问题是计算从 s 到 d 的最短路径。
故而我们用用 d(v) 表示从 s 到顶点 v 的最短距离,则可得到如下递归关系和基始赋值:

那么根据上述的递归关系式,我们在编程实现中可以采用递归和迭代两种方式,如果采用递归的话,因为从源点到目的点有着许多条路径,而其中很多路径其本身就是有部分重叠的,以递归的方式实现的话,有许多节点是会被重复计算的,二期出入栈带来的时间损耗也较大;故而我们可以考虑采用迭代的方式,从源点开始,逐节点计算,但这就涉及一个问题,节点的计算顺序如何确定,观察后我们可以知道,迭代计算dv之前,是需要先计算v的每个前驱节点u的值d(u),故而我们需要依据前驱节点的关系对图的节点进行一个排序,针对于有向无环图,可以通过拓扑排序实现。
2.拓扑排序
拓扑排序是指将所有顶点排成一个顶点序列,使得每个顶点都在其前驱顶点之后,即边的方向都是从左向右,如下图所示,为上述图的拓扑排序结果:

那么拓扑排序要如何实现呢?实际上其是基于图的深度优先搜索算法的,深度优先搜索的目标是尽可能深的搜索,尽可能多的连接图中的顶点,并且在需要的时候分支;其基本思路就是以一个顶点为起点,先搜索其邻居节点,而后递归的又以其邻居节点为起点,继续搜索其邻居节点的邻居节点,直到以该节点为根节点的子树搜索完毕;可以预见的是,如果仅仅是不加约束的搜索邻居节点,会有着很多重复的操作,因为有些节点的邻居节点之间也是相连的,比如以s为起点,搜索到其邻居节点a和b,而后递归的以邻居节点a为起点进行搜索,则又会搜索到b,那么b会被重复计算两次;故而为了解决这个问题,我们对每个节点引入状态标志,即‘w’(white)表示该节点并没有被搜索过,‘g’(gray)表示该节点正在被访问,‘b’(black)表示该节点的所有邻居节点都已经被访问过了,即基于该节点的深度优先搜索树已经构建完毕了;基于上述思路,可以写出相应的dfs_visit(now_vertex, L)函数:
代码清单4-dfs_visit

def dfs_visit(self, now_vertex, L):
now_vertex.status = 'g' # 正在访问
# 对于该节点的所有邻居节点
for connectedto in now_vertex.getconnectedto():
if connectedto.status == "w":
connectedto.prefix = now_vertex # 标记前置节点
# 递归搜索
self.dfs_visit(connectedto, L)
now_vertex.status = 'b'
L.append(now_vertex)在理解了深度优先搜索之后,我们就可以以其为基础实现拓扑排序了,其基本思路是:遍历图中的所有顶点,并对白色顶点调用dfsvisit方法,并更改相应的dfsvisit函数,引入拓扑排序列表,将完成搜索的节点加入列表L中。
而之所以遍历所有顶点,而不是简单的从一个指定的顶点开始搜索,是因为这样能够确保深度优先搜索森林中的所有顶点都被考虑在内,毕竟很多深度优先树是会进入死路的,即其并没有包括图的完整节点。
这里只对白色节点调用dfs_visit函数,则是可以避免很多冗余操作,比如节点A是节点B的前驱节点,对节点A进行深度搜索时必然会对节点B也进行搜索,那么就AB而言,最终的拓扑排序列表必然是以节点A为起始的;故而此时,后续再对B节点的访问就是冗余的操作,可以省略,此时最终的拓扑排序列表也不会更新;那么针对于联通的有向无环图,最终输出的拓扑排序列表必然是一个从源节点开始包含列表所有节点的完整序列,而当循环遍历到该源节点时,可以预见的是后续L将不会在更新,因为所有的节点都被访问过了,状态都不再是‘w’了。
代码清单5-topological_sort

def topological_sort(self):
for now_vertex in self.vertexlist.values():
now_vertex.status = 'w' # 未访问
now_vertex.prefix = None
L = []
for now_vertex in self.vertexlist.values():
# 对所有的节点都执行dfs_visit 是因为生成的深度优先树会有多课,因为会有许多进入死路的
# 此处的判断对于最终的拓扑排序输出起到很重要的作用,同样的其也节省了许多不必要的冗余计算,因为深度搜索其本质时对一个节点尽可能的往下搜索
# 那么比如节点A是节点B的前驱节点,对节点A进行深度搜索时必然会对节点B也进行搜索,那么最终输出的拓扑排序列表也必然是由A产生,而不是由B产生的
# 故而此时,对B节点的访问就是冗余的操作,可以省略,此时相应的拓扑排序列表也不会更新;
# 那么针对于联通的有向无环图,最终输出的拓扑排序列表必然是一个从源节点开始包含列表所有节点的完整序列,而当循环遍历到该节点时,可以预见的是
# 后续L将不会在更新,因为所有的节点都不再是‘w’了。
if now_vertex.status == 'w':
self.dfs_visit(now_vertex, L)
L.reverse()
return L完成拓扑排序后,结合之前的递归表达式,我们即可从源节点开始,按照拓扑顺序,逐个计算每个顶点d(v)。
3.有向无环图的单源最短路径实现
代码清单6-DAG_shortest_paths
# 以迭代的方式实现单源最短路径,迭代的方式,那么就需要按前驱节点的顺序进行求解,只有当某个节点其前驱节点的值都求解而出时,才可以继续求解
def DAG_shortest_paths(self, graph):
L = graph.topological_sort() # 节点列表集合
for vector in L:
print(vector.key)
vector.distance = inf
L[0].distance = 0
for i in range(1, len(L)):
current_vector = L[i]
paths_min = inf
vector_recoder = L[0]
'''
最短路径中的子路径是其端点间的最短路径
d(v)= min{d(u)+w(u,v)}
递归调用或则迭代形式,迭代形式则在计算d(v)时,需要计算出其每个前驱节点u的值d(u)
'''
for vectorfrom in current_vector.connectedfrom:
paths = vectorfrom.distance + current_vector.connectedfrom[vectorfrom]
if paths < paths_min:
paths_min = paths
vector_recoder = vectorfrom
current_vector.distance = paths_min
current_vector.prefix = vector_recoder
for vector in L:
print(vector.distance)
self.getPath(L[len(L) - 1])
def getPath(self, destination): # destination是结束的单词的顶点对象
# 从树的叶节点往上层找,直到找到根节点
print(destination.key)
while destination.prefix is not None:
print(destination.prefix.key)
destination = destination.prefix在DAG_shortest_paths算法种,拓扑排序的运行时间为O(m+n),而计算d(v)的步骤运行时间为O(m),故而总的时间复杂度为O(m+n),代码执行结果如下:

四:一般有向图的单源最短路径问题
1.有向无环图与一般有向图的实践区别
针对于有向无环图,我们可以通过动态规划实现对单源最短路径的求解,那么针对于一般有向图,该方法是否还适用呢?我们考虑如下的两个图:

以图a为例,该图包含的环是正环,那么最短路径就是良定义的,也是可求的;但如果是b图,因为其包含了一个负圈,负圈的不断循环会使得数值越来越小,即不存在一个最短路径。我们首先以良定义的图a分析,继续按照有向无环图方式进行推理,我们会发现a和b互为彼此的前驱节点,那么沿用之前的递归表达式,会得到:
d(a)=min{3,3+d(b),4+d(e)}
d(b)=min{5,-2+d(a),1+d(c)}
也就是说d(a)和d(b)的计算互相依赖,形成一个循环死局,针对于这种问题,一般的思路而言,要么跟着这个循环走,观察其规律;要么,引入限制条件,将这个圈给打破。
2.定义更细的子问题,打破循环,引入决策步数
节点的求解和循环的执行都是按步骤来的,故而我们可以引入表述该决策步数的变量;将问题转换为求一个从s到t的不超过n-1条边的简单路径;那么在第一步对t做决策时,由于t有两个前驱节点c和d,故而相应的需要在下面的两个决策项中做最优选择:
- 从c到t:剩下的子问题就时计算从s到达c的,最多有n-2条边的最短路径
- 从d到t:剩下的子问题就时计算从s到达d的,最多有n-2条边的最短路径
于是,我们将子问题的一般形式定义为:计算从s到v的,最多包含k条边的最短路径,其长度记为:d(v,k)。接下来,我们构建d(v,k)之间的递归关系:
首先,我们以d(a,k)为例,进行分析:

- d(a,1) 表示从s经过一步到a的最短路径,在图中即为s-a,长度为3.
- d(a,2) 表示从s经过两步到a的最短路径,在图中即为s-b-a,长度为8,其没有d(a,1)小,故而d(a,2)= d(a,1)=3
- d(a,3) 表示从s经过三步到a的最短路径,在图中即为s-b-e,长度为8,或者为s-a-b-a,长度为4,其也没有d(a,2)小,故而d(a,3)= d(a,2)= d(a,1)=3
- d(a,4)进一步分析,即为s-b-a-b-a,该路径进一步经过了负圈,使得d变大,而且在其之后的d也会更大。
3. Bellman_Ford算法
故而我们对上述例子反映的规律进行总结:假设最后一步是从前驱节点u到达a,则剩下的子问题就是“从s经过最多k-1条边到达a”:
![]()
而同时,值得注意的是定义是:最多包含k条边的最短s-a路径,那也就是说会存在k-1,k-2,,,1条边,使得路径最小,就如上述的a,其d(a,k)实际上是d(a,1)最小;即递归表达式改为:
![]()
进一步分析,我们可以发现d(v,k-1)其实已经包含了d(v,k-2)以及之前的所有相关值,故而简化得到最终表达式:
![]()
根据递归表达式,我们采用迭代方式实现如下:
代码清单7-Bellman_ford

算法的整体目标在于填写完成相应的opt(v,k)表格,算法的大体执行思路如下:首先获取传进来的图的相关属性,此处给出构建带环一般有向图的实现:
代码清单8-build_graph_normal_cycle
def build_graph_normal_cycle(self, type):
Nodes = ['s', 'a', 'b','c', 'e', 't']
positive_circle = [['s', 's', 'a', 'a', 'b', 'b', 'c', 'c', 'e', 'e'],
['a', 'b', 'b', 'c', 'a', 'e', 'b', 't', 'a', 't'],
[3, 5, -2, -2, 3, -1, 1, 7, 4, 9]]
negative_cycle = [['s', 's', 'a', 'a', 'b', 'b', 'c', 'c', 'e', 'e'],
['a', 'b', 'b', 'c', 'a', 'e', 'b', 't', 'a', 't'],
[3, 5, -3, -2, 2, -3, 1, 7, 4, 9]]
if type == 'positive':
cycle = positive_circle
elif type == 'negative':
cycle = negative_cycle
side_num = len(positive_circle[0])
g = Graph()
for node in Nodes:
g.addVertex(node)
for i in range(side_num):
g.addEdge(cycle[0][i], cycle[1][i], cycle[2][i])
return g而后初始化opt(v,k)=inf 源顶点s: opt(s,k) = 0 (经过k步从s到s最短都为0,不考虑负圈),并将每一个节点的前继节点赋为None;而后迭代求解d(v,k),我们按决策步数依节点求解,计算完每个节点在相应步数下的最短路径后,将产生该路径的邻居节点赋为该节点的前继节点,以方便后续的回溯。
4.带负圈检测的Bellman_Ford算法
现在上述的求解都是基于正圈的,而如果一般有向图中存在负圈,那么求解得到的最短路径将是错误的,那么负圈如何判断?对于n个节点的图而言,我们的k是只需要到迭代至n-1即可的,因为一条连接n个节点的最短路径其包含的边只有n-1条,故而我们为了检测负圈,我们将迭代步数增加至n。如果新的路径中包含正圈,因为最小的约束,该新路径是不会被采用的,也就是说其全局最短路径的值是不会随着迭代步数的增加而改变的;但是针对于存在负圈的有向图而言,经过负圈的路径都会得到缩小,也就是说相应的opt(v,k)的值是会小的,故而我们可以依据d(v,n-1)与d(v,n)是否有差异来判别是否存在s可达的负权重环。
我们对负圈检测的理论基础进行进一步的阐述:对于包含负权重环的图G来说,其必定存在一些顶点v,使得d(v,n)比d(v,n-1)小,假设图中包含一个圈为l的环,同时存在一个节点v,在不经过圈的时候,只需要n-l边即可抵达,那么只考虑该圈而且无其他路径的的情况下,经过n-l+1条边到达该点的最短路径仍然还是d(v,n-l),但是经过n条边的时候,其因为会经过该负圈(l),将使得最小值进一步减少;使得d(v,n)比d(v,n-1)小;也就是说假如d(v,n)比d(v,n-1)小,则必定是因为发现了一条s-v的恰好包含n条边的更短路径p,由于路径p中有n条边,则必定存在环;从p中去除环,得到的新路径p‘,而p’的长度至少是d(v,n-1),比d(v,n)要大,因此此环必定是负权重环。
代码清单9-Bellman_ford 包含负圈检测以及路径回溯
def Bellman_ford(self, graph, s):
"""
s 为起始节点
d(v,k) = min{d(v,k-1),min{d(u,k-1)+w(u,v)}}
d(v,k)表示的是从s开始至多经过k-1步到达v,其可以表示为从s开始经过至多k-1步就已经到达v和至多经过k-1步到达v的前驱节点,并取最小
"""
# 初始化d[v][k]以及前继节点
negative_cycle = False
vertex_num = graph.vertexnum
# 以字典形式进行描述,字典的键为相应的节点,其值为一个列表,存放不同k下的值
opt = {}
# 初始化opt(v,k)=inf 源地点s opt(s,k) = 0 (经过k步从s到s最短都为0,不考虑负圈)
for vertex in graph.vertexlist.values():
opt[vertex.key] = [inf for _ in range(vertex_num + 1)]
vertex.prefix = None
opt[s] = [0 for _ in range(vertex_num + 1)]
# 迭代求解 d【v,k】
for k in range(1, vertex_num + 1):
for vertex in graph.vertexlist.values():
if vertex.key == s:
opt[vertex.key][k] = 0
else:
# 计算前驱节点最小值
from_paths_min = inf
for vectorfrom in vertex.connectedfrom:
# 该节点的前驱节点的最短距离+两个节点之间的距离
from_paths = opt[vectorfrom.key][k - 1] + vertex.connectedfrom[vectorfrom]
# 动态规划表达式
from_paths_min = min(opt[vertex.key][k - 1], from_paths, from_paths_min)
# 确定该节点的前驱节点 以方便回溯
if from_paths_min == from_paths:
vertex.prefix = vectorfrom
opt[vertex.key][k] = from_paths_min
# 打印相应的opt(v,k)表格
for opt_k in opt.values():
print(opt_k)
'''
负圈检测此处关注的时,可能而对存在 s 可达的负权重环的图 G2 来说,必定存在一些顶点 v(比如环中顶点a),(此处的必定对于圈很大的图是否成立,
是否可能会找到一个图使得d(v,n)与d(v,n-1)皆相同,但后续的不同)比如图中包含一个圈为l的环,同时存在一个节点v,在不经过圈的时候,
只需要n-l边即可抵达,那么只考虑该圈而且无其他路径的的情况下,经过n-l+1条边到达该点的最短路径仍然还是d(v,n-l),但是经过n条边的时候,
其就必然会产生不同,因为会经过该负圈(l),使得最小值进一步减少;使得 d(v, n) 比 d(v, n − 1) 小。
因此,我们可以依据d(v, n) 与 d(v, n − 1) 是否有差异来判别是否存在 s 可达的负权重环。假如 d(v, n) 比 d(v, n − 1) 更小,
则必定是因为发现了一条 s-v 的“恰好”包含 n 条边的更短路径 p;由于路径 p 中有 n 条边,则必定存在环;
从 p 中去除环,得到新的路径 p′,而 p′的长度至少是 d(v, n − 1),比 d(v, n)要大,因此此环必定是负权重环
'''
if opt_k[vertex_num] != opt_k[vertex_num - 1]:
negative_cycle = True
# 打印相应的最短路径顺序
if negative_cycle:
print("Found negative cycle")
else:
# 注意此处的’t'是人为规定的目的点,但其实计算该点时,
# 相应的其他点也得到了计算,可以获得以任何节点为尾部的回溯路径
self.getPath(graph.vertexlist['t'])
return opt对图a和b分别执行上述结果,可得到相应的结果如下:


5.Bellman_Ford算法中的第一类冗余
动态规划算法的迭代实现相较于递归实现执行速度已经得到了极大的提升,但如果我们进一步观察相应的opt表格,可以发现在正向计算OPT值表时,其中还是有许多不必要的计算单元,故而我们可以通过观察规律将这些冗余计算进行避免。
首先,对包含正圈的OPT值表进行观察,可以看出其表格中有很多重复的值,每一行都是在某个特定值后,其后面的值就都不再变化了,而不变的值的计算是冗余的,是可以忽略的;那么这些冗余单元的出现位置有何特点呢?可以发现,其都出现在每一列的最小单元之后,准确的说是扣除一些单元之后的最小单元。
为了严格描述这一点,我们引入下述描述:(距离s不超过k条边的最近顶点)考虑包含n个顶点的无负边有向图,以及起始顶点s,对于k=1,。。。n-1,定义vk*为除v0*,。。。vk-1*之外,距离s不超过k条边的最近顶点,其中v0*=s。同时相应的,我们可以证明最小单元与其右侧单元具有相同的值,即:d(v,k)表示从k出发,经过不超过k条边到达顶点v的最短距离,则有:
![]()
综上所述,我们这样描述BELLMAN-FORD算法中的第一类冗余:在边的权重都是正数这一条件下,令集合S表示最短距离已经确定的点,也就是第k列中的最小单元vk*,在后续的计算中,无需考虑S中的顶点,只需考虑不在S中的顶点即可。
代码清单10-Faster_Bellman_ford 第一类冗余去除

def Faster_Bellman_ford(self,graph,s):
'''
规律发现:
第一类冗余:
在扣除一些单元之后的每一列的最小单元确定后,可以发现其之后的单元的值都不再改变,即这些都为冗余单元,可以将上述进行一个准确的描述,即
距离s(起点)不超过k条边的最近顶点:考虑包含n个顶点的无负边有向图,以及起始节点s,对于k=1,...n-1,定义Vk*为除V0*,,,Vk-1*之外,
距s不超过k条边的最近顶点,其中V0*=s;那么基于此,可以定义每一列的最小单元:第k的最小单元,就是距s不超过k条边的最近顶点;同时可以证明
最小单元与其右侧单元具有相同的值即:d(Vk*,k)=d(Vk*,k+1)=...=d(Vk*,n-1)
在边的权重都是正数这一条件下,令集合S表示最短距离已经确定的点,也就是第k列中的最小单元VK*,在后续的计算中,无需考虑S中的顶点,
只需考虑不在S中的顶点即可
第二类冗余:
不仅每一列最小单元的右侧有着冗余,其实每一列最小单元的左侧也有者部分冗余,实际而言,第二列的最小单元只能是前两列最小单元的邻居之一,
即在计算过程中,每一步只需要考虑与S中顶点相邻的那些顶点即可
当Bellman_Ford去除上述两类冗余之后,其本质上就已经演化成Dijkstra算法了!!
'''
vertex_num = graph.vertexnum
# 以字典形式进行描述,字典的键为相应的节点,其值为一个列表,存放不同k下的值
opt = {}
explored_nodes = {'s':0}
unexplored_nodes = []
# 初始化opt(v,k)=inf 源地点s opt(s,k) = 0 (经过k步从s到s最短都为0,不考虑负圈)
for vertex in graph.vertexlist.values():
opt[vertex.key] = [inf for _ in range(vertex_num + 1)]
unexplored_nodes.append(vertex.key)
vertex.prefix = None
opt[s] = [0 for _ in range(vertex_num + 1)]
unexplored_nodes.remove('s')
# 迭代求解 d【v,k】
for k in range(1, vertex_num):
for vertex in graph.vertexlist.values():
# 对节点是否在S中进行判断,已经在S中的节点不需要再进行计算
if vertex.key in unexplored_nodes:
# 计算前驱节点最小值
from_paths_min = inf
# 去除第一类冗余,已经得到的距离s(起点)不超过k条边的最近顶点,后续k+1就不再进行计算
for vectorfrom in vertex.connectedfrom:
# 该节点的前驱节点的最短距离+两个节点之间的距离
from_paths = opt[vectorfrom.key][k - 1] + vertex.connectedfrom[vectorfrom]
# 动态规划表达式
from_paths_min = min(opt[vertex.key][k - 1], from_paths, from_paths_min)
# 确定该节点的前驱节点 以方便回溯
if from_paths_min == from_paths:
vertex.prefix = vectorfrom
opt[vertex.key][k] = from_paths_min
min_k = inf
# 确定去除某些单元之后的每一列的最小单元
for vertex in unexplored_nodes:
if opt[vertex][k] < min_k:
min_k = opt[vertex][k]
min_vertex = vertex
# 将距离s不超过k条边的最近顶点加入集合S,并移除未探索节点集合
unexplored_nodes.remove(min_vertex)
explored_nodes[min_vertex]=min_k
# 打印相应的opt(v,k)表格
for opt_k in opt.values():
print(opt_k)
# 注意此处的’t'是人为规定的目的点,但其实计算该点时,
# 相应的其他点也得到了计算,可以获得以任何节点为尾部的回溯路径
print(explored_nodes)
self.getPath(graph.vertexlist['t'])
return opt6.Bellman_Ford算法的第二类冗余
在去除第一类冗余之后,我们继续观察可以发现不仅每一列最小单元的右侧有着冗余,其实每一列最小单元的左侧也有者部分冗余,实际而言,第二列的最小单元只能是前两列最小单元的邻居之一,即在计算过程中,每一步只需要考虑与S中顶点相邻的那些顶点即可。那么当我们将这两类冗余都去除之后,改进的Bellman_ford算法实际上已经简化为Dijkstra算法了!!
7.去除两类冗余的Bellman_Ford算法 == Dijkstra算法
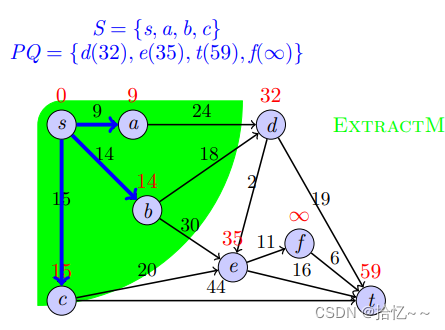
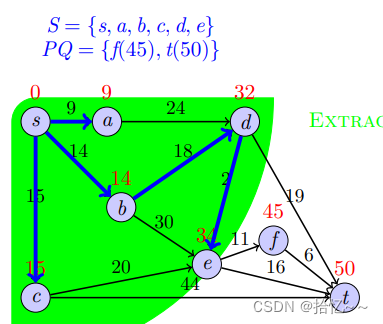
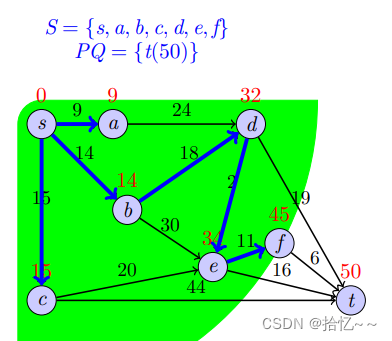
Dijkstra算法是一个贪心算法,其不断重复“找S的最近邻居节点并加入S,依据新加入的节点更新其他节点的最短距离估计值”这两个步骤,直至计算出所有节点的最短路径,其中S表示的是距s最短距离已知的顶点集合;相应的伪代码和实现如下:
代码清单11-Dijkstra(self, graph, s)

def Dijkstra(self, graph, s):
"""
无负边有向图上单源最短路径
初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”
从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,
从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
后续可以结合优先队列(Fibonacci堆对其进行加速),优先队列是一种支持“在一些动态变化的的数中找最小的数”的数据结构
"""
vertex_num = graph.vertexnum
# 以字典形式进行描述,字典的键为相应的节点,其值为最短距离值
shortest_distance = {}
# 已经探索的节点集合
explored_nodes = []
unexplored_nodes= []
# 初始化opt(v)=inf 源地点s opt(s,k) = 0 (经过k步从s到s最短都为0,不考虑负圈)
for vertex in graph.vertexlist.values():
shortest_distance[vertex.key] = inf
unexplored_nodes.append(vertex.key)
shortest_distance[s] = 0
while len(explored_nodes) != vertex_num:
# select the unexplored node v* (v* not belong S) that minimizes d(v)
min_distance = inf
for node in unexplored_nodes:
if shortest_distance[node]<min_distance:
min_distance_flag = node
min_distance = shortest_distance[min_distance_flag]
# 最短距离上界最小的邻接点,取S所有邻接点的最小值
explored_nodes.append(min_distance_flag)
unexplored_nodes.remove(min_distance_flag)
# 依据新加入的节点更新其他节点的最短距离估计值
# 对所有已经探索过的节点,更新其一步可以到达的节点的最短值。
for node in explored_nodes:
for adjacent_node in graph.vertexlist[node].connectedto:
shortest_distance[adjacent_node.key] = min(shortest_distance[adjacent_node.key],
shortest_distance[node]+graph.vertexlist[node]
.connectedto[adjacent_node])
print(shortest_distance)我们以一个例子来说明上述算法的具体实现过程:
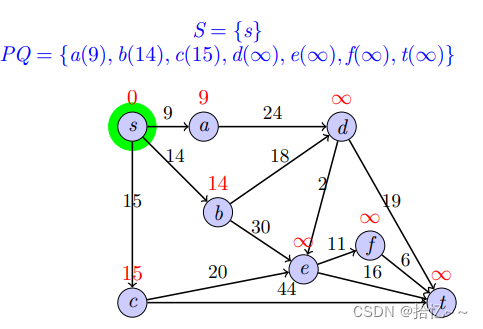

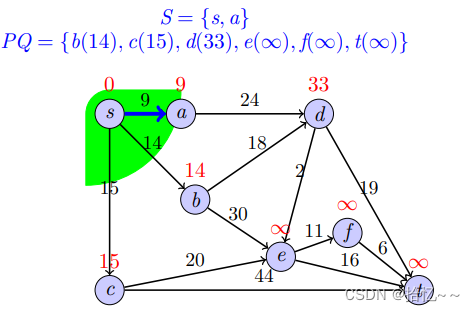

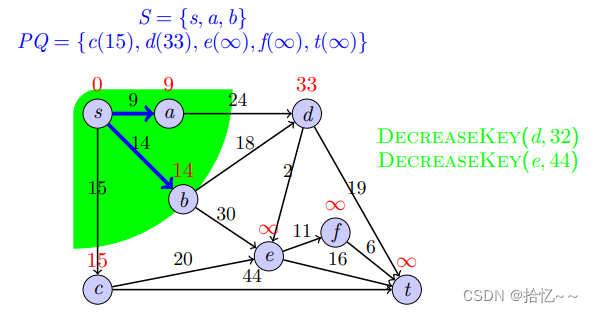


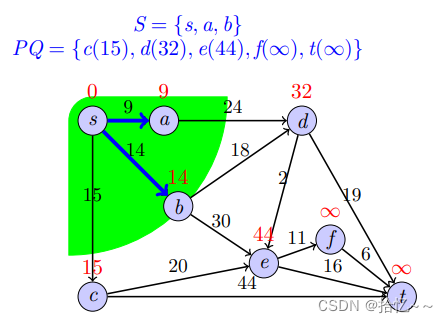






























 4004
4004











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








