机器学习线性回归算法——原理+python详细代码解析（sklearn）

python机器学习ML

已于 2024-08-21 11:23:40 修改

阅读量468

点赞数 13

分类专栏：机器学习算法文章标签：机器学习算法 python 线性回归 sklearn 数据分析人工智能

于 2024-08-21 10:57:28 首次发布

本文链接：https://blog.csdn.net/qq_45932996/article/details/141387511

版权

机器学习算法专栏收录该内容

1 篇文章 0 订阅

订阅专栏

线性回归算法作为经典的机器学习算法之一，拥有极为广泛的应用范围，深受业界人士的青睐。该算法主要用于研究分析响应变量如何受到特征变量的线性影响。其通过构建回归方程，借助各特征变量对响应变量进行拟合，并且能够利用回归方程进行预测。鉴于线性回归算法较为基础、简单，所以比较容易入门。

一、线性回归算法的基本原理

线性回归算法是一种较为基础的机器学习算法，基于特征（自变量、解释变量、因子、协变量）和响应变量（因变量、被解释变量）之间存在的线性关系。

线性回归算法的数学模型为：y=α+β1x1+β2x2+…+βnxn+ε

矩阵形式为：y=α+Xβ+ε

假定特征之间无多重共线性；误差项εi（i=1,2,…,n）之间相互独立，且均服从同一正态分布N(0,σ2)，σ2是未知参数，误差项满足与特征之间的严格外生性假定，以及自身的同方差、无自相关假定。响应变量的变化可以由α+Xβ组成的线性部分和随机误差项i两部分解释。对于线性模型，一般采用最小二乘估计法来估计相关的参数，基本原理是使残差平方和最小，残差就是响应变量的实际值与拟合值之间的差值。

二、案例讲解

我们用于分析的数据是“数据4.1”文件，它是XX生产制造企业1994－2021年的profit（营业利润水平）、invest（固定资产投资）、labor（平均职工人数）、rd（研究开发支出）数据。下面我们以profit为响应变量，以invest、labor、rd为特征变量，开展线性回归算法。

1　导入分析所需要的模块和函数

导入pandas、numpy、matplotlib、seaborn、statsmodels、sklearn等模块。其中，pandas、numpy用于数据读取、数据处理、数据计算；matplotlib.pyplot、seaborn、sklearn中的LinearRegression用于构建线性回归模型；train_test_split用于把样本随机划分为训练样本和测试样本；mean_squared_error、r2_score模块分别用于计算均方误差（MSE）和可决系数，评价模型优劣。

import pandas as pd#载入pandas模块，并简称为pd
import numpy as np#载入numpy模块，并简称为np
import matplotlib.pyplot as plt#载入matplotlib.pyplot模块，并简称为plt
import seaborn as sns#载入seaborn模块，并简称为sns

from sklearn.linear_model import LinearRegression#载入LinearRegression模块
from sklearn.model_selection import train_test_split#载入train_test_split模块
from sklearn.metrics import mean_squared_error, r2_score#载入mean_squared_error, r2_score模块

2　数据读取及观察

首先需要将提供的数据文件【回复：数据4.1】放入安装Python的默认路径位置，并从相应位置进行读取，在Spyder代码编辑区输入以下代码并运行：

data=pd.read_csv('C:/Users/Administrator/.spyder-py3/数据4.1.csv')  # 读取数据4.1.csv文件

注意，因用户的具体安装路径不同，设计路径的代码会有差异，用户可以在“文件”窗口查看路径及文件对应的情况，如图。建议这样复制绝对路径，否则报错，找不到文件路径。

data.info()  # 观察数据信息。运行结果为：

数据集中共有25个样本（25 entries, 0 to 24）、5个变量（total 5 columns）。5个变量分别是year、profit、invest、labor、rd，均包含25个非缺失值，其中year、labor的数据类型为整数型（int64），profit、invest、rd的数据类型为浮点型（float64）。数据文件中共有3个浮点型（float64）变量、2个整型（int64）变量，数据内存为1.1KB。

3　描述性分析

在进行数据分析时，当研究者得到的数据量很小时，可以通过直接观察原始数据来获得所有的信息。但是，当得到的数据量很大时，就必须借助各种描述性指标来完成对数据的描述工作。用少量的描述性指标来概括大量的原始数据，对数据展开描述的统计分析方法被称为描述性统计分析。

data.describe()#对数据集进行描述性分析
data.describe().round(2)#只保留两位小数
data.describe().round(2).T#只保留两位小数并转置
data.mean()#对数据集中的变量求均值
data.var()#对数据集中的变量求方差
data.std()#对数据集中的变量求标准差
data.cov()#对数据集中的变量求协方差矩阵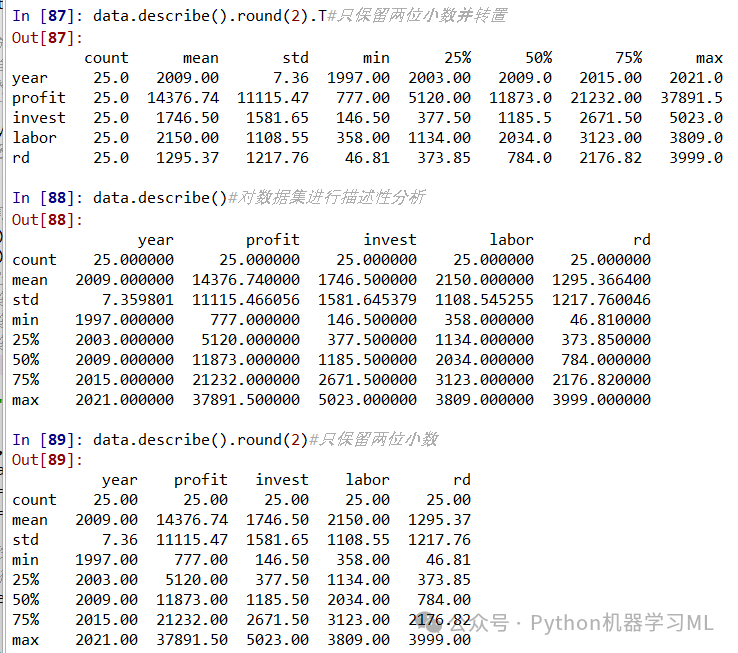

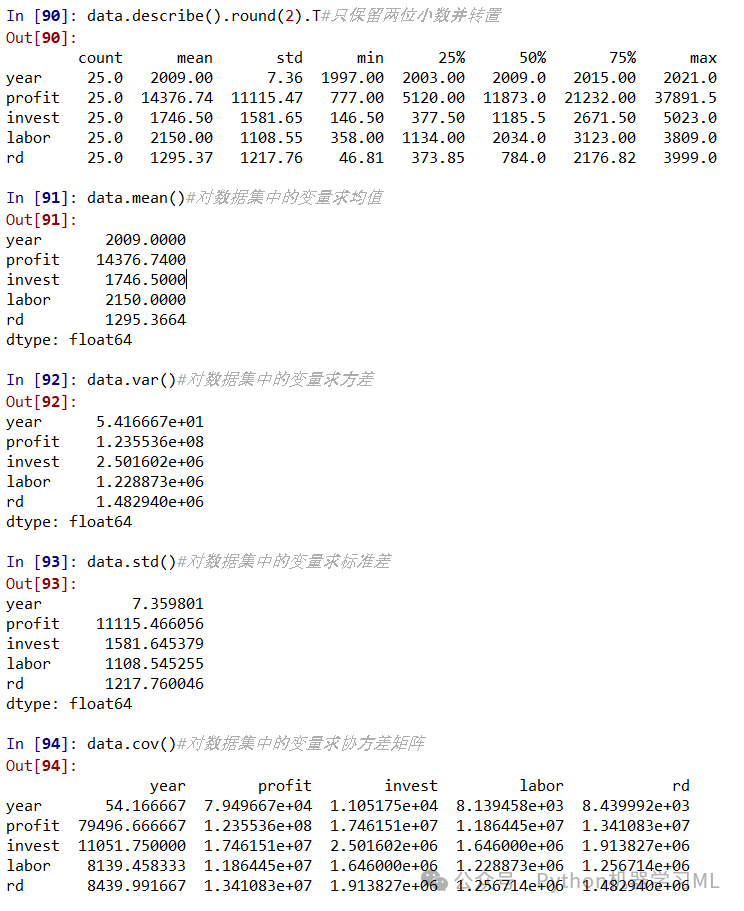
描述性分析的常用函数

4 相关性分析

相关性分析通过计算皮尔逊相关系数、斯皮尔曼等级相关系数、肯德尔秩相关系数展开。其中皮尔逊相关系数是一种线性关联量度，适用于变量为定量连续变量且服从正态分布、相关关系为线性时的情形。如果变量不是正态分布的，或具有已排序的类别，相互之间的相关关系不是线性的，则更适合采用斯皮尔曼等级相关系数和肯德尔秩相关系数。

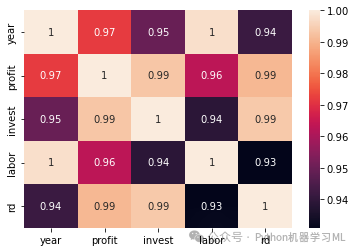
5　使用sklearn进行线性回归完整代码

1.使用验证集法进行模型拟合


import pandas as pd#载入pandas模块，并简称为pd
import numpy as np#载入numpy模块，并简称为np
import matplotlib.pyplot as plt#载入matplotlib.pyplot模块，并简称为plt
import seaborn as sns#载入seaborn模块，并简称为sns

from sklearn.linear_model import LinearRegression#载入LinearRegression模块
from sklearn.model_selection import train_test_split#载入train_test_split模块
from sklearn.metrics import mean_squared_error, r2_score#载入mean_squared_error, r2_score模块


data=pd.pd.read_csv(filepath+'数据4.1.csv')
data.info()
print(data)
X = data.loc[:, ["invest","labor","rd"]]#将数据集中的第4列至第5列作为自变量
print(X)
y = data.loc[:,"profit"] #将数据集中的第2列作为因变量 
print(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)#将样本示例全集划分为训练样本和测试样本，测试样本占比为30%。
X_train.shape, X_test.shape, y_train.shape, y_test.shape#观察四个数据的形状
print(X_train)
model = LinearRegression()#使用线性回归模型
model.fit(X_train, y_train)#基于训练样本拟合模型
model.coef_#计算上步估计得到的回归系数值
model.score(X_test, y_test)#观察模型在测试集中的拟合优度（可决系数）
pred = model.predict(X_test)#计算响应变量基于测试集的预测结果
print(pred)
pred.shape#观察数据形状 
mean_squared_error(y_test, pred)#计算测试集的均方误差
r2_score(y_test, pred)#计算测试集的可决系数

2 更换随机数种子，使用验证集法进行模型拟合

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=100)#更换随机数种子
model = LinearRegression().fit(X_train, y_train)#基于训练样本拟合线性回归模型
pred = model.predict(X_test)#计算响应变量基于测试集的预测结果
mean_squared_error(y_test, pred)#计算测试集的均方误差
r2_score(y_test, pred)#计算测试集的可决系数

3 使用10折交叉验证法进行模型拟合

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import RepeatedKFold
X = data.loc[:, ["invest","labor","rd"]]#将数据集中的第4列至第5列作为自变量
y = data.loc[:,"profit"] #将数据集中的第2列作为因变量 
model = LinearRegression()#使用线性回归模型
kfold = KFold(n_splits=10,shuffle=True, random_state=1)#将样本示例全集分为10折
scores = cross_val_score(model, X, y, cv=kfold)#计算每一折的可决系数
scores#显示每一折的可决系数
scores.mean().round(3)#计算各折样本可决系数的均值
scores.std().round(3)#计算各折样本可决系数的标准差
scores_mse = -cross_val_score(model, X, y, cv=kfold, scoring='neg_mean_squared_error')#得到每个子样本的均方误差
scores_mse#显示各折样本的均方误差
scores_mse.mean()#计算各折样本均方误差的均值
# 更换随机数种子，并与上步得到结果进行对比，观察均方误差MSE大小
kfold = KFold(n_splits=10, shuffle=True, random_state=100)
scores_mse = -cross_val_score(model, X, y, cv=kfold, scoring='neg_mean_squared_error')#得到每个子样本的均方误差
scores_mse.mean()#计算各折样本均方误差的均值
r2_score(y_test, pred)#计算测试集的可决系数

4 使用10折重复10次交叉验证法进行模型拟合

rkfold = RepeatedKFold(n_splits=10, n_repeats=10, random_state=1)
scores_mse = -cross_val_score(model, X, y, cv=rkfold, scoring='neg_mean_squared_error')#得到每个子样本的均方误差
scores_mse.shape
scores_mse.mean()
# 绘制各子样本均方误差的直方图
sns.distplot(pd.DataFrame(scores_mse))
plt.xlabel('MSE')
plt.title('10-fold CV Repeated 10 Times')

5 使用留一交叉验证法进行模型拟合

loo = LeaveOneOut()
scores_mse = -cross_val_score(model, X, y, cv=loo, scoring='neg_mean_squared_error')
scores_mse.mean()

三、总结

一、线性回归算法的优点

简单易懂
线性回归算法的原理相对简单直观，容易理解和解释。它通过建立特征变量与响应变量之间的线性关系，以简洁的数学表达式来描述这种关系，使得人们能够快速掌握其核心思想。对于初学者来说，线性回归是机器学习入门的良好选择，有助于建立对数据分析和建模的基本认识。
计算效率高
线性回归的计算过程相对高效。在数据量不是特别巨大的情况下，其训练和预测的速度通常较快。这使得线性回归算法在处理实时性要求较高的任务或大规模数据的初步分析中具有优势，可以快速得到结果并进行决策。
可解释性强
线性回归模型的系数可以直接反映特征变量对响应变量的影响程度和方向。例如，一个正的系数表示该特征变量与响应变量正相关，即特征变量的值增加时，响应变量的值也倾向于增加；反之，负的系数表示负相关。这种可解释性对于实际应用中理解数据和做出决策非常重要，特别是在一些对结果解释性要求较高的领域，如金融、医疗等。

二、线性回归算法的缺点

假设限制
线性回归算法假设特征变量与响应变量之间存在线性关系。然而，在现实世界中，很多数据之间的关系可能是非线性的。如果数据的真实关系不符合线性假设，那么线性回归模型可能无法准确地捕捉到这种关系，从而导致模型的性能下降。
对异常值敏感
线性回归模型对异常值比较敏感。一个或几个异常值可能会对模型的参数估计产生较大的影响，从而改变回归直线的位置和斜率。这可能导致模型的预测结果不准确，尤其是当异常值的数量相对较多时。
多重共线性问题
当特征变量之间存在高度相关性时，即存在多重共线性问题，线性回归模型的性能也会受到影响。在这种情况下，模型的系数估计可能变得不稳定，难以准确地反映各个特征变量对响应变量的独立影响。此外，多重共线性还可能导致模型的方差增大，降低预测的准确性。

python机器学习ML

关注

13
点赞
踩
16

收藏

觉得还不错? 一键收藏
0
评论
机器学习线性回归算法——原理+python详细代码解析（sklearn）

线性回归算法作为经典的机器学习算法之一，拥有极为广泛的应用范围，深受业界人士的青睐。该算法主要用于研究分析响应变量如何受到特征变量的线性影响。其通过构建回归方程，借助各特征变量对响应变量进行拟合，并且能够利用回归方程进行预测。鉴于线性回归算法较为基础、简单，所以比较容易入门。线性回归算法是一种较为基础的机器学习算法，基于特征（自变量、解释变量、因子、协变量）和响应变量（因变量、被解释变量）之间存在的线性关系。线性回归算法的数学模型为：y=α+β1x1+β2x2+…+βnxn+ε。
复制链接

扫一扫