gradient 梯度 ，Sobel、Canny、Seam Carving

gradient，Sobel、Canny、Seam Carving

---

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

---

提示：代码能直接跑的，放图片文章过长了，想看哪个图 直接imshow吧

一、图片求梯度

1. 需要理解导数、微分、偏导数、梯度、差分，间有何区别。
2. 连续函数的偏导数：
   
   对于离散数据，用差分近似偏导数。 近似表示时，又有向前、向后、中心差分等
   

---

二、Sobel

https://homepages.inf.ed.ac.uk/rbf/HIPR2/sobel.htm

1. sobel的核
   Sobel算子结合了高斯平滑和微分操作，能够减少噪声的影响，在一定程度上保持了边缘的连续性和定位精度。

x方向的核：

y方向的核：

---

三、Canny

1. 算法流程

1. smoothing
2. gradient
3. Non-maximum suppression：线性插值，将软边缘变成硬边缘
4. Linking and thresholding：设置max, min 高于上阈值的当作真边缘，低于min当作假边缘，处于中间的，看周围是否有和真边缘连接，有则保留。

2. 代码实现

1. smooth

def smooth(im, gauss_kernel):
    W, H = im.shape
    k_size = gauss_kernel.shape[0]
    new_gray = np.zeros([W - k_size + 1, H - k_size + 1])
    for i in range(W - k_size):
        for j in range(H - k_size):
            new_gray[i, j] = np.sum(im[i: i+k_size, j: j+k_size] * gauss_kernel)
    return new_gray

2. gradients

def gradients(im, x_kernel, y_kernel):
    W, H = im.shape

    if(x_kernel.shape[0] != y_kernel.shape[0]):
        print("x_kernel.shape[0] != y_kernel.shape[0]")
        exit(1)
    k_size = x_kernel.shape[0]

    dx = np.zeros([W - k_size + 1, H - k_size + 1])
    dy = np.zeros([W - k_size + 1, H - k_size + 1])
    M  = np.zeros([W - k_size + 1, H - k_size + 1])

    for i in range(W - k_size):
        for j in range(H - k_size):
            dx[i, j] = np.sum(im[i: i+k_size, j: j+k_size] * x_kernel)
            dy[i, j] = np.sum(im[i: i+k_size, j: j+k_size] * y_kernel)
            M[i, j] = np.sqrt(np.square(dx[i, j]) + np.square(dy[i, j]))

    return dx, dy, M

3. Non-maximum suppression

def NMS(M, dx, dy):
    d = np.copy(M)
    W, H = M.shape
    NMS = np.copy(d)
    NMS[0, :] = NMS[W - 1, :] = NMS[:, 0] = NMS[:, H - 1] = 0
    for i in range(1, W - 1):
        for j in range(1, H - 1):
            if M[i, j] == 0:
                NMS[i, j] = 0
            else:
                gradX = dx[i, j]
                gradY = dy[i, j]
                gradTemp = d[i, j]
                if np.abs(gradY) > np.abs(gradX):
                    weight = np.abs(gradX) / np.abs(gradY)
                    grad2 = d[i - 1, j]
                    grad4 = d[i + 1, j]
                    if gradX * gradY > 0:
                        grad1 = d[i - 1, j - 1]
                        grad3 = d[i + 1, j + 1]
                    else:
                        grad1 = d[i - 1, j + 1]
                        grad3 = d[i + 1, j - 1]
                else:
                    weight = np.abs(gradY) / np.abs(gradX)
                    grad2 = d[i, j - 1]
                    grad4 = d[i, j + 1]
                    if gradX * gradY > 0:
                        grad1 = d[i + 1, j - 1]
                        grad3 = d[i - 1, j + 1]
                    else:
                        grad1 = d[i - 1, j - 1]
                        grad3 = d[i + 1, j + 1]

                gradTemp1 = weight * grad1 + (1 - weight) * grad2
                gradTemp2 = weight * grad3 + (1 - weight) * grad4
                if gradTemp >= gradTemp1 and gradTemp >= gradTemp2:
                    NMS[i, j] = gradTemp
                else:
                    NMS[i, j] = 0
    return NMS

4. thresholding

def double_threshold(NMS, minval, maxval):
    W, H = NMS.shape
    DT = np.zeros([W, H])
    TL = minval * np.max(NMS)
    TH = maxval * np.max(NMS)

    for i in range(1, W - 1):
        for j in range(1, H - 1):
            if (NMS[i, j] < TL):
                DT[i, j] = 0
            elif (NMS[i, j] > TH):
                DT[i, j] = 1
            elif (NMS[i - 1, j - 1:j + 1] < TH).any() or (
                    NMS[i + 1, j - 1:j + 1].any() or (NMS[i, [j - 1, j + 1]] < TH).any()):
                DT[i, j] = 1
    return DT

main

import cv2
import numpy as np
import os

# 生成高斯核
def gaussian_kernel_2d(size, sigma_x, sigma_y=None):
    if sigma_y is None:
        sigma_y = sigma_x

    x, y = np.meshgrid(np.linspace(-(size//2), size//2, size),
                       np.linspace(-(size//2), size//2, size))

    kernel_2d = (1 / (2 * np.pi * sigma_x * sigma_y)) * np.exp(-(x ** 2 / (2 * sigma_x ** 2) + y ** 2 / (2 * sigma_y ** 2)))

    # 归一化核
    kernel_2d /= kernel_2d.sum()

    return kernel_2d

if __name__ == '__main__':
    list_path=""
    list_data=os.listdir(list_path)
    gauss_kernel = gaussian_kernel_2d(3, 2)

    x_kel = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
    y_kel = np.array([[1, 2, 1], [0, 0, 0], [-1, -2, -1]])

    for i in list_data:
        im_path=list_path+"/"+i
        im=cv2.imread(im_path,cv2.IMREAD_GRAYSCALE)

        new_im=smooth(im, gauss_kernel)
        cv2.imwrite("./{}_smooth.jpg".format(i),new_im)
        x,y,M=gradients(new_im,x_kel,y_kel)
        cv2.imwrite("./{}_x.jpg".format(i),x)
        cv2.imwrite("./{}_y.jpg".format(i),y)
        cv2.imwrite("./{}_M.jpg".format(i),M)
        non_maxima=NMS(M,x,y)
        result=double_threshold(non_maxima, 0.3, 0.8)
        cv2.imwrite("./{}".format(i),result*255)

---

四、Seam Carving

个人比较喜欢这个，可以很方便的对图片的尺寸进行修改

https://karthikkaranth.me/blog/implementing-seam-carving-with-python/

流程

1. smooth
2. “energy” as gradient magnitude
   
3. 在8邻域内，找到一条能量最小的缝，将其去除

公式3.2：

4. 重复2-3 ，直到满足条件

代码实现

1. smooth
   由于算子用的是sobel,可以

def smooth(im, gauss_kernel):
    W, H = im.shape
    k_size = gauss_kernel.shape[0]
    new_gray = np.zeros([W - k_size + 1, H - k_size + 1])
    for i in range(W - k_size):
        for j in range(H - k_size):
            new_gray[i, j] = np.sum(im[i: i+k_size, j: j+k_size] * gauss_kernel)
    return new_gray

2. energy
   这里加了padding = 1

def gradients(im, x_kernel, y_kernel,padding=1):
    W, H = im.shape

    if(x_kernel.shape[0] != y_kernel.shape[0]):
        print("x_kernel.shape[0] != y_kernel.shape[0]")
        exit(1)
    k_size = x_kernel.shape[0]
    out_row = W - k_size + 2*padding + 1
    out_col = H - k_size + 2*padding + 1
    padded_input = np.pad(im, padding, mode='constant')

    dx = np.zeros([out_row, out_col])
    dy = np.zeros([out_row, out_col])
    energy_map  = np.zeros([out_row, out_col])

    for i in range(out_row):
        for j in range(out_col):
            dx[i, j] = np.sum(padded_input[i: i+k_size, j: j+k_size] * x_kernel)
            dy[i, j] = np.sum(padded_input[i: i+k_size, j: j+k_size] * y_kernel)
            energy_map[i, j] = np.sqrt(np.square(dx[i, j]) + np.square(dy[i, j]))
    return energy_map

3. 计算各个seam的能量
   计算各个列的能量，M的最后一行为 公式3.2 的求和。

def calculate_seam(img):
    energy_map = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    energy_map = gradients(energy_map, np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
                           , np.array([[1, 2, 1], [0, 0, 0], [-1, -2, -1]]))
    rows, cols = energy_map.shape

    M = energy_map.copy()
    backtrack = np.zeros_like(M, dtype=np.int32)

    for i in range(1, rows):
        for j in range(0, cols):
            if j == 0:
                idx = np.argmin(M[i - 1, j:j + 2])
                backtrack[i, j] = idx + j
                min_energy = M[i - 1, idx + j]
            else:
                idx = np.argmin(M[i - 1, j - 1:j + 2])
                backtrack[i, j] = idx + j - 1
                min_energy = M[i - 1, idx + j - 1]

            M[i, j] += min_energy

    return M, backtrack

找到能量最小的一列，将其去除。

def carve_column(img):
    rows, cols, _ = img.shape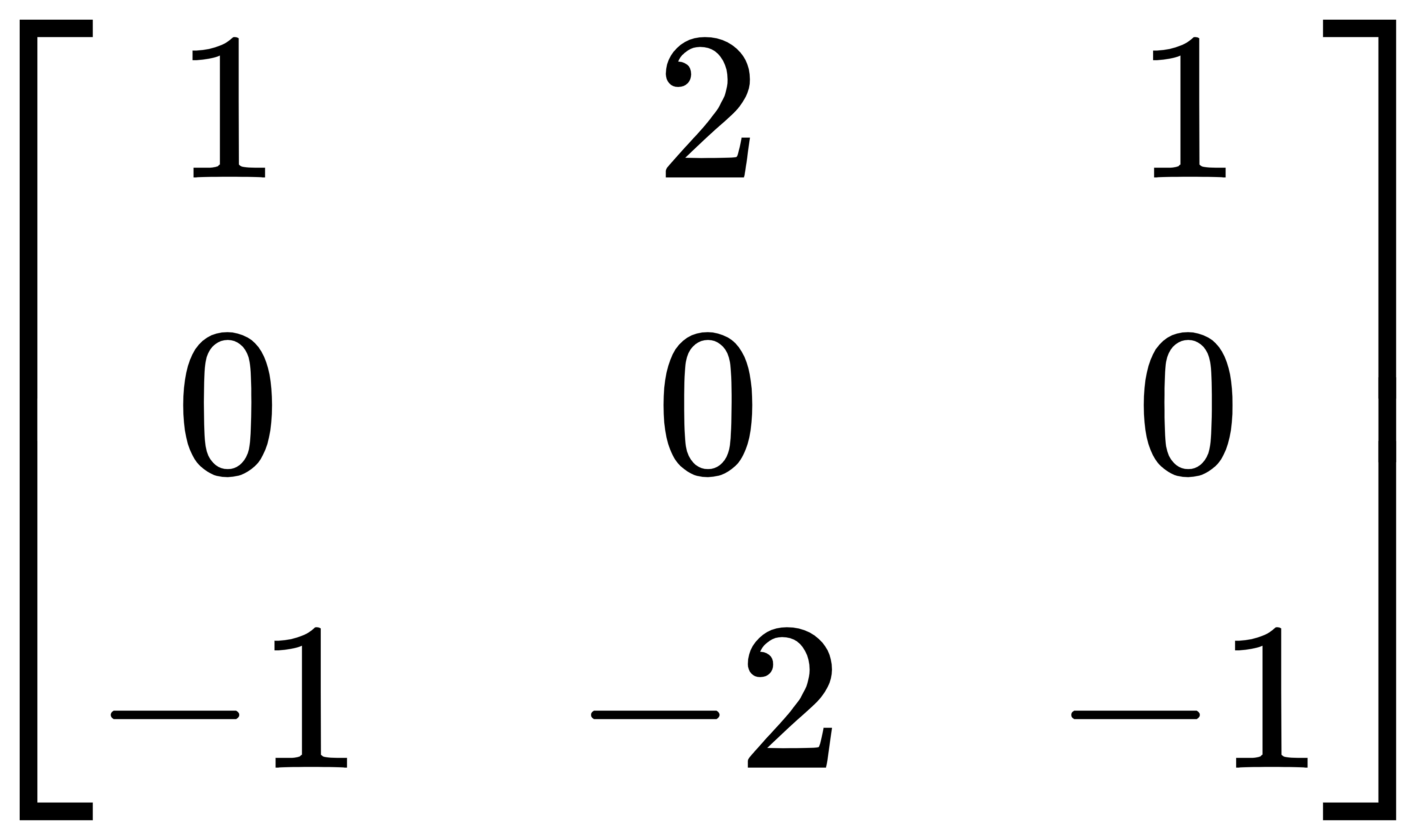![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/0b6542feecb14a2a9351a71ef06708df.png#pic_center)


    M, backtrack = calculate_seam(img)
    mask = np.ones((rows, cols), dtype=np.bool_)
    # mask = np.zeros_like(img) #需要imshow的话，可以用该mask,或者直接对原图像进行操作
    j = np.argmin(M[-1])

    for i in reversed(range(rows)):
        mask[i, j] = False
        # mask[i, j, 1] = 255
        j = backtrack[i, j]

    mask = np.stack([mask] * 3, axis=2)
    img = img[mask].reshape((rows, cols - 1, 3))

    return img

4. 以上步骤，已经完成column的一列去除。
   时间复杂度还是很高的，也能通过一次计算能量图后，将前几个低能量的列直接去除。

---