机器学习实验之不同含量果汁饮料的聚类（K-Means）

K-Means 实操项目：不同含量果汁饮料的聚类

【实验内容】

某企业通过采集企业自身流水线生产的一种果汁饮料含量的数据集，来实现K-Means算法。通过聚类以判断该果汁饮料在一定标准含量偏差下的生产质量状况，对该饮料进行类别判定。

【数据集】

该数据集共有样本59个，变量2个，包括juice（该饮料的果汁含量偏差）、sweet（该饮料的糖分含量偏差），单位均为mg/ml。

所有特征变量都为与标准含量相比的偏差，该数据集没有目标类别标签变量。

【实验要求】

1.加载数据集，读取数据，探索数据。（数据集路径：data/data76878/4_beverage.csv）

2.样本数据转化（可将pandasframe格式的数据转化为数组形式），并进行可视化（绘制散点图），观察数据的分布情况，从而可以得出k的几种可能取值。

3.针对每一种k的取值，进行如下操作：

（1）进行K-Means算法模型的配置、训练。

（2）输出相关聚类结果，并评估聚类效果。

这里可采用CH指标来对聚类有效性进行评估。在最后用每个k取值时评估的CH值进行对比，可得出k取什么值时，聚类效果更优。

注：这里缺乏外部类别信息，故采用内部准则评价指标（CH）来评估。 (metrics.calinski_harabaz_score())       

（3）输出各类簇标签值、各类簇中心，从而判断每类的果汁含量与糖分含量情况。

（4）聚类结果及其各类簇中心点的可视化（散点图），从而观察各类簇分布情况。（不同的类表明不同果汁饮料的果汁、糖分含量的偏差情况。）

4.【扩展】（选做）：设置k一定的取值范围，进行聚类并评价不同的聚类结果。

参考思路：设置k的取值范围；对不同取值k进行训；计算各对象离各类簇中心的欧氏距离，生成距离表；提取每个对象到其类簇中心的距离，并相加；依次存入距离结果；绘制不同看、值对应的总距离值折线图。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn import metrics

加载数据集，读取数据，探索数据

data = pd.read_csv("./datasets/4_beverage.csv")
print(data)
print(data.shape)

     juice   sweet
0   2.1041  0.8901
1  -1.0617 -0.4111
2   0.3521 -1.7488
3  -0.1962  2.5952
4   1.4158  1.0928
5  -0.3951 -1.3293
6   1.4717 -1.6269
7   1.1289  1.9430
8  -1.3395  1.4619
9  -1.7840  0.7658
10  0.2253 -1.6511
11 -1.7436 -0.8622
12  1.3344  0.7974
13 -1.5782  1.5956
14  1.5828 -1.9999
15 -1.3934 -1.5497
16  1.2468 -1.5924
17 -1.2568 -2.1163
18  0.9322  1.5899
19 -1.5856  1.6365
20  1.4471 -1.9076
21 -1.2813 -1.1420
22  1.7455  1.4376
23 -1.2829 -1.0061
24  1.6665  1.9916
25 -0.8084  1.7866
26  1.1403 -1.2797
27 -1.3256 -1.5516
28  1.1607  1.5775
29 -0.8429  1.4698
30  0.4698 -2.0118
31 -1.8372 -1.1305
32  1.0231  1.3676
33 -1.5947  1.4925
34  2.1863  1.4717
35 -1.2897 -0.2397
36  0.9445 -1.9819
37 -0.3994  0.7870
38  1.4183  1.6716
39 -1.9189 -1.6785
40  1.0484  1.6938
41 -1.3545  0.3926
42  1.6835  0.9819
43 -1.0607  1.3211
44  1.1648 -1.5882
45 -1.6424 -1.7862
46  1.5457  1.2446
47 -1.5979  1.4422
48  1.1682 -1.9737
49 -0.8932  1.2771
50  1.0951 -0.9530
51 -1.7017 -1.3891
52  0.8891  1.9404
53 -0.8442  1.1151
54  1.2965 -1.0272
55 -2.0036 -1.6035
56 -1.8810 -1.2161
57  1.7710  1.3894
58 -0.8684  2.1205
(59, 2)

样本数据转化（可将pandasframe格式的数据转化为数组形式），并进行可视化（绘制散点图），观察数据的分布情况，从而可以得出k的几种可能取值

npdata = np.array(data) # 转化成numpy数组
x = data.iloc[:, 0 : 1]
y = data.iloc[:, 1 : 2]
plt.scatter(x, y)  # 绘制散点图
plt.show()

for n_clusters in range(3,10):
    # 进行K-Means算法模型的配置、训练
    kmeans = KMeans(n_clusters)  # 构建聚类器
    kmeans.fit(npdata)
    # 输出相关聚类结果，并评估聚类效果
    y_predict=kmeans.predict(npdata)
    score=metrics.calinski_harabasz_score(npdata,y_predict)
    print('{1} 准确率:{0:f}'.format(score,n_clusters))  #显示准确率
    # 输出各类簇标签值、各类簇中心，从而判断每类的果汁含量与糖分含量情况
    markers = ['*', 'v', '+', '^', 's', 'x', 'o','1','2','3','4']      # 标记样式列表
    colors = ['r', 'g', 'm', 'c', 'y', 'b', 'orange','black','skyblue']  # 标记颜色列表
    labels = kmeans.labels_      # 获取聚类标签
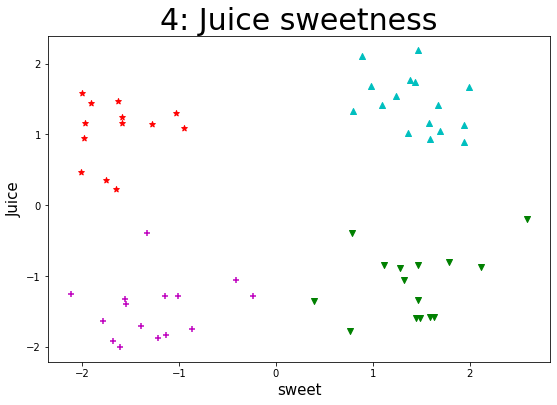
    # 聚类结果及其各类簇中心点的可视化（散点图），从而观察各类簇分布情况
    plt.figure(figsize=(9, 6))
    plt.title('{0}: Juice sweetness'.format(n_clusters),fontsize=30)
    plt.xlabel('sweet',fontsize=15)
    plt.ylabel('Juice',fontsize=15)
    for i in range(n_clusters):
        members = labels == i      # members是一个布尔型数组
        plt.scatter(
            npdata[members, 1],      # 城市经度数组
            npdata[members, 0],      # 城市纬度数组
            marker = markers[i],   # 标记样式
            c = colors[i]          # 标记颜色
        )   # 绘制散点图
    
    
    

3 准确率:73.959867
4 准确率:188.066731
5 准确率:166.399894
6 准确率:156.117815
7 准确率:149.989669
8 准确率:157.312805
9 准确率:160.865889

关注公众号 布沃布图 ，后台回复 机器学习实验 获取源码