2.1 递归的概念
1、递归算法
递归算法:直接或者间接调用自身的算法称为递归算法。
2、适合递归算法的问题
- 递归函数:用函数自身给出定义的函数。
- 递归结构:二叉树。
- 可以转化为递归算法解决。
3、典型递归程序示例


4、递归算法设计的一般步骤

5、递归解决实际问题-汉诺塔问题


# include<stdio.h>
void move(char a, char b){
printf("从%c移到%c\n", a, b);
}
void hanoi(int n, char a, char b, char c){
if(n == 0){
return;
}
else{
hanoi(n-1, a, c, b);
move(a, b);
hanoi(n-1, c, b, a);
}
}
int main(){
char a = 'a';
char b = 'b';
char c = 'c';
hanoi(10, a, b, c);
}
下面内容与上面是同样的思路:
递归关系:
- 1、将n-1个盘子从from -> buffer
- 2、将1个盘子从from -> to
- 3、将n-1个圆盘从buffer -> to
终止条件:
- 4、递归结束的条件是,只有一个盘子时,只需一次移动操作即可。
public class hanoi {
public static void move(int n, String from, String buffer, String to) {
//第一步:递归结束的条件
if (n == 1) {
System.out.println("from " + from + " to " + to);
return;
}
// n-1 个圆盘从 from -> buffer
move(n - 1, from, to, buffer);
//将 1 个圆盘从 from -> to
move(1, from, buffer, to);
//将 n-1 个圆盘从 buffer -> to
move(n - 1, buffer, from, to);
}
public static void main(String[] args) {
hanoi.move(3, "石柱1", "石柱2", "石柱3");
}
}
下面是在网上看到的关于递归的理解,感觉说的挺好的。


6、递归解决实际问题-排列问题





7、递归优缺点
- 优点:结构清晰,可读性强,而且容易用数学归纳法来证明算法的正确性,因此它为设计算法、调试程序带来很大方便。
- 缺点:递归算法的运行效率较低,无论是耗费的计算时间还是占用的存储空间都比非递归算法要多。
2.2 分治法的基本原理
1、分治法所解决问题的特征
1、原问题的规模缩小到一定的程度就可以容易地解决;
2、原问题可以分解为若干个规模较小的相同子问题;
3、合并子问题的解可以得到原问题的解;
4、子问题之间相互独立,即不同子问题不包含公共子问题。
2、分治法解决问题的基本思想
1、分解原问题:原问题分解成多个子问题
2、解决子问题:递归地求解各个子问题
3、合并问题解:将结果合并为原问题解
注意事项:1、子问题与原问题性质完全相同;2、子问题之间相互独立,可分别求解;3、最小子问题可直接求解。
3、分治算法的基本框架

4、分治法的复杂性分析

2.3 分治法解集合运算
1、分治法示例-将数组元素升序排列

2、问题一:求数组中的最大值
问题一:n个元素存放在一维数组A中,试用分治法求A中元素的最大值。

时间复杂度:O(n)
#include<cstdio>
int max(int A[], int low, int high){
if(low == high){
return A[low];
}else{
int mid = (low + high) / 2;
int a = max(A, low, mid);
int b = max(A, mid+1, high);
if(a > b){
return a;
}else{
return b;
}
}
}
int main(){
int A[] = {8, 6, 5, 4, 3, 9, 7, 1, 2};
printf("数组的最大值是:%d", max(A, 0, 8));
}
运行结果:

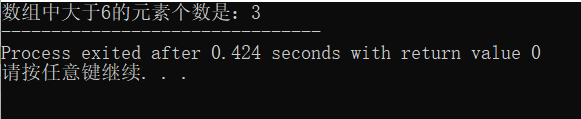
3、问题二:求数组中大于x的元素个数
问题二:n个整数存放在一维数组A中,试用分治法求A中大于x的元素个数。

时间复杂度:O(n)
#include<cstdio>
int com(int A[], int low, int high, int x){
if(low == high){
if(A[low] > x){
return 1;
}else{
return 0;
}
}
int mid = (low + high) / 2;
int a = com(A, low, mid, x);
int b = com(A, mid+1, high, x);
return a+b;
}
int main(){
int A[] = {8, 6, 5, 4, 3, 9, 7, 1, 2};
printf("数组中大于6的元素个数是:%d", com(A, 0, 8, 6));
}
运行结果:
2.4 大整数乘法
问题描述:n位10进制整数X和Y,由于X和Y位数较大,若直接做乘法运算则可能会内存溢出,如何求X和Y的乘积?

计算策略:模拟竖式计算乘法过程,先用整型数组X,Y分别表示两个n位10进制整数,其中X[0]表示位数,X[1]表示正负号,X[2]是个位数,X[3]是十位数,依次类推;然后逐位相乘再相加得到X和Y乘积,最后将结果存放到Z数组。按这种策略计算的时间复杂度为O(n²)。






2.5 Strassen矩阵乘法


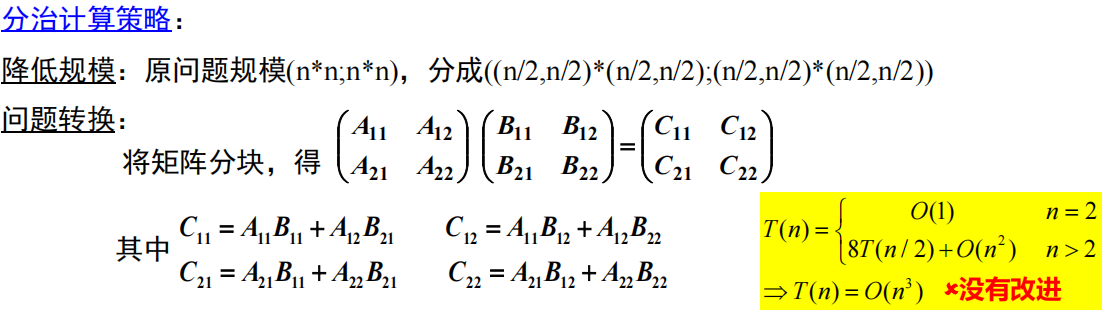




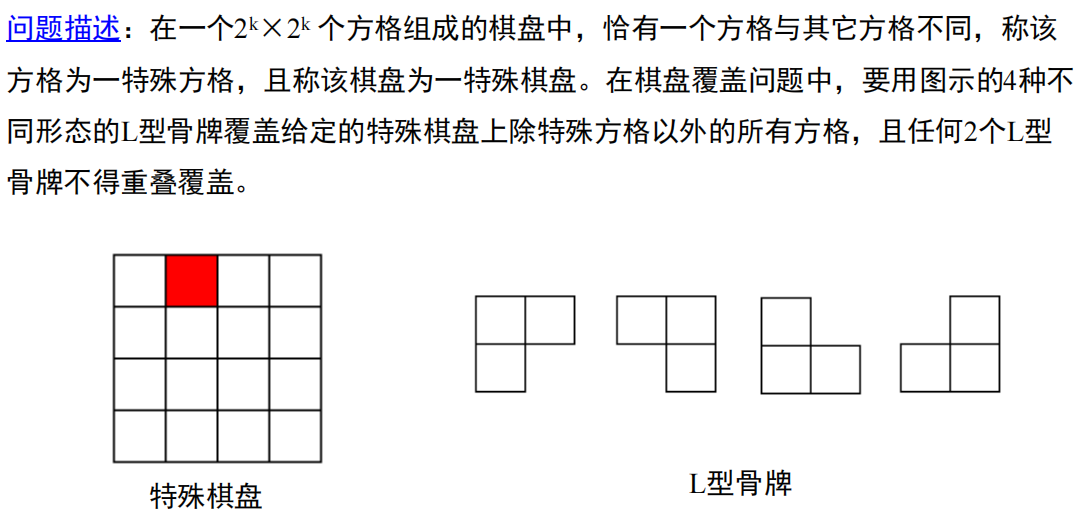
2.6 棋盘覆盖问题








2.7 分治法进行排序
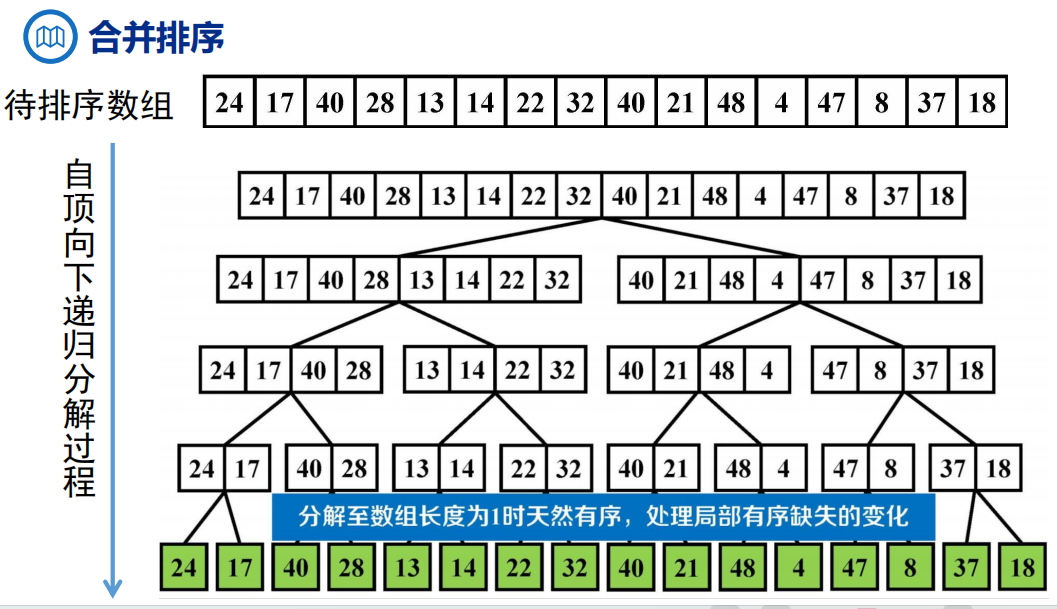
1、合并排序
基本思想:将待排序元素分成大小大致相同的两个子集合,分别对两个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
基本操作:
- 分:分成大小大致相同的子集合。
- 治:分别对两个子集合进行排序。
- 合:将排好序的子集合合并成一个有序的集合。



2、快速排序



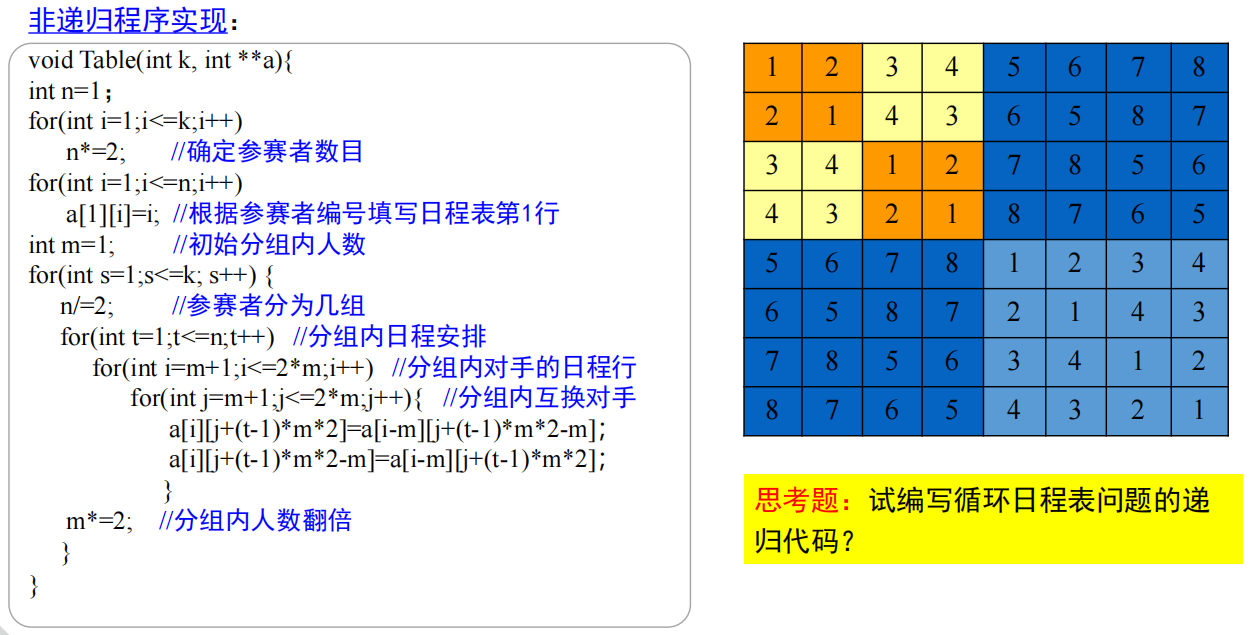
2.8 循环赛日程表



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










