MIT-归并排序和快速排序

问题描述

将一组无序的元素按某种顺序（通常是升序或降序）排列的过程。

例子

输入：arr = [5, 2, 9, 1, 5, 6]
输出：arr = [1, 2, 5, 5, 6, 9]

算法实现

冒泡排序（暴力排序）

冒泡排序是一种简单的排序算法，其核心思想是：通过不断交换相邻的元素，将较大的元素“冒泡”到数组的末尾，直到整个数组有序。

1. 从数组的第一对元素开始，比较相邻的两个元素。如果前一个元素大于后一个元素，则交换它们。
2. 继续比较下一对元素，直到比较到数组的末尾，这样每一轮结束时，最大的元素会被“冒泡”到数组的末尾。
3. 对剩下的未排序部分继续重复步骤1和步骤2，直到整个数组排序完成。

假设我们有一个数组：

arr = [5, 2, 9, 1, 5, 6]

第一轮：

• 比较 5 和 2，交换它们，得到 [2, 5, 9, 1, 5, 6]。
• 比较 5 和 9，不交换。
• 比较 9 和 1，交换它们，得到 [2, 5, 1, 9, 5, 6]。
• 比较 9 和 5，交换它们，得到 [2, 5, 1, 5, 9, 6]。
• 比较 9 和 6，交换它们，得到 [2, 5, 1, 5, 6, 9]。

第一轮结束时，最大的元素 9 被“冒泡”到数组的最后一位。

第二轮：

• 比较 2 和 5，不交换。
• 比较 5 和 1，交换它们，得到 [2, 1, 5, 5, 6, 9]。
• 比较 5 和 5，不交换。
• 比较 5 和 6，不交换。

第二轮结束时，第二大的元素 6 被“冒泡”到数组倒数第二位。

第三轮：

• 比较 2 和 1，交换它们，得到 [1, 2, 5, 5, 6, 9]。
• 比较 2 和 5，不交换。
• 比较 5 和 5，不交换。

第三轮结束时，第三大的元素 5 被“冒泡”到数组的倒数第三位。

第四轮：

• 比较 1 和 2，不交换。

此时数组已经排序完成，结果为：

[1, 2, 5, 5, 6, 9]

void bubbleSort(int &A[], int n)
{
		for (int i = 0; i < n - 1; i ++ )  // 后 i 个数已经有序
		{
				bool isSwap = false;	
				for (int j = 0; j < n - i - 1; j ++ )
				{
					if (A[j] > A[j + 1]) swap(A[j], A[j + 1]), isSwap = true;
				}
				if (isSwap) break;
		}
}

时间复杂度：$O(n^2)$

---

归并排序（分治）

归并排序法是将两个(或两个以上)有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

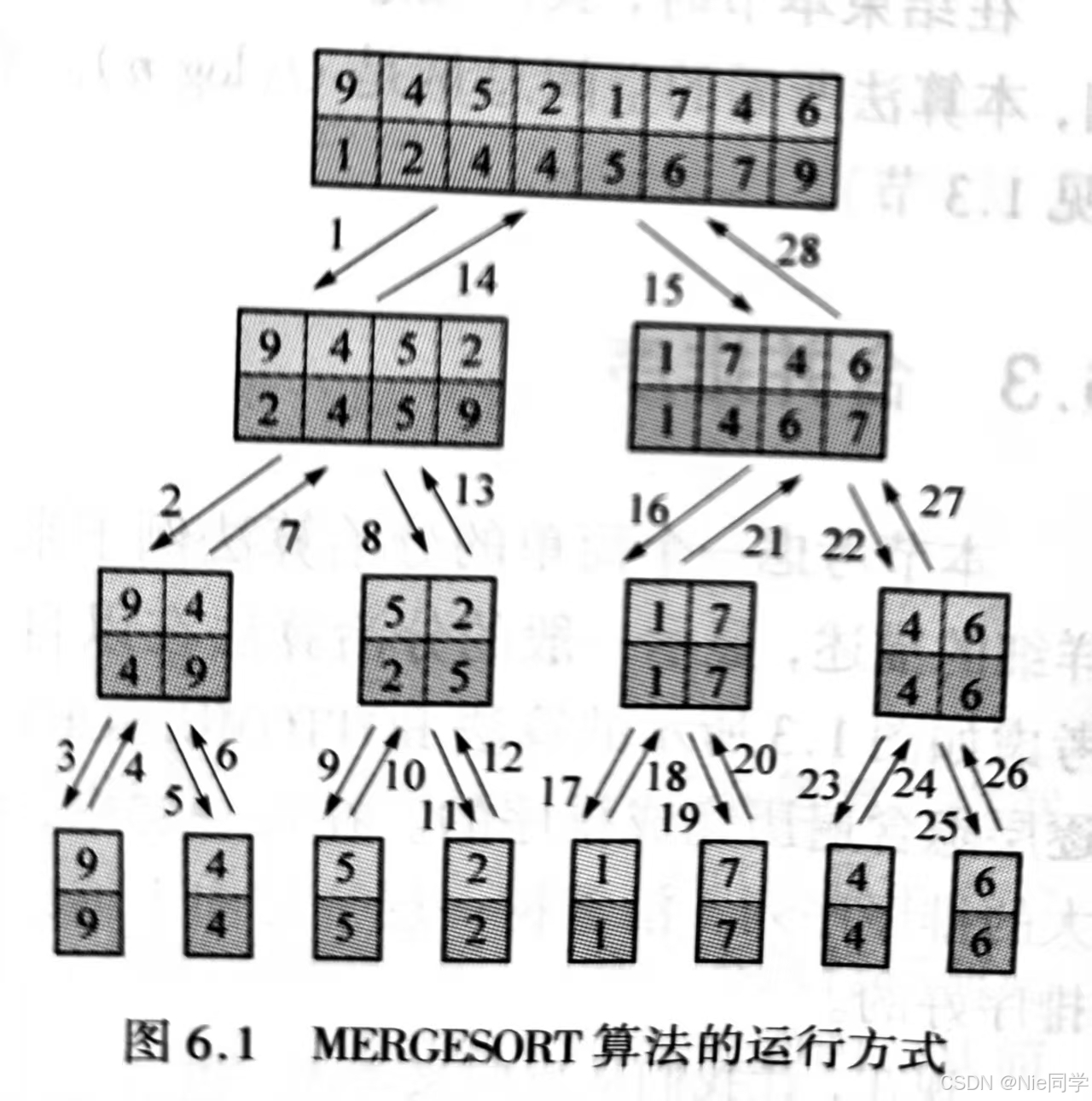
void mergeSort(int &A[], int low, int high)
{
		if (low >= high) return;
		
		int mid = (low + high) / 2;
		
		mergeSort(A, low, mid);  // 左边
		mergeSort(A, mid + 1, high); // 右边
		Merge(A, low, mid, high); // 合并
}

void Merge(int &A[], int low, int mid, int high)
{
		int n = high - low + 1;
		int B[n];
		int i = 0;
		int l = low, r = mid + 1;

		while (l <= mid && r <= high)
		{
				if (A[l] < A[r]) B[i ++ ] = A[l ++ ];
				else B[i ++ ] = B[r ++ ];
		}

		while (l <= mid) B[i ++ ] = A[l ++ ];
		while (r <= high) B[i ++ ] = B[r ++ ];

		for (i = 0; i < n; i ++ )
				A[low + i] = B[i];
}

时间复杂度：$O(n{\log }_{2}n)$

假设 $n=2^h$ 且 $T(1)=O(1)$，$T(n)$ 是执行一次大小为 $n$ 次的 mergeSort 所需的时间。

• mergeSort(A, low, mid)：$T(\frac{n}{2})$
• mergeSort(A, mid + 1, high)：$T(\frac{n}{2})$
• Merge(A, low, mid, high)：$O(n)$

$$\begin{array}{rl}T(n)& =2T(\frac{n}{2})+O(n)\\ & \le 2T(\frac{n}{2})+cn\\ & \le 2\left[2T(\frac{n}{2^2})+c\frac{n}{2}\right]+cn\\ & =2^{2}T(\frac{n}{2^2})+2cn\\ & \le ...\\ & =2^{h}T(\frac{n}{2^h})+hcn\\ & =nT(1)+cn{\log }_{2}n\\ & =O(n{\log }_{2}n)\end{array}$$

---

快速排序（分治）

给定一个中轴元素 $A[w]$，在待排序的数组 $A[low,high]$ 通过划分、比较和交换，使得：

• $A[low,w-1]<A[w]$
• $A[w]>A[w+1,high]$

其中 $i$ 是当前数组最后一个小于中轴元素 $A[w]$ 的下标；$j$ 是当前数组最后一个大于中轴元素 $A[w]$ 的下标。

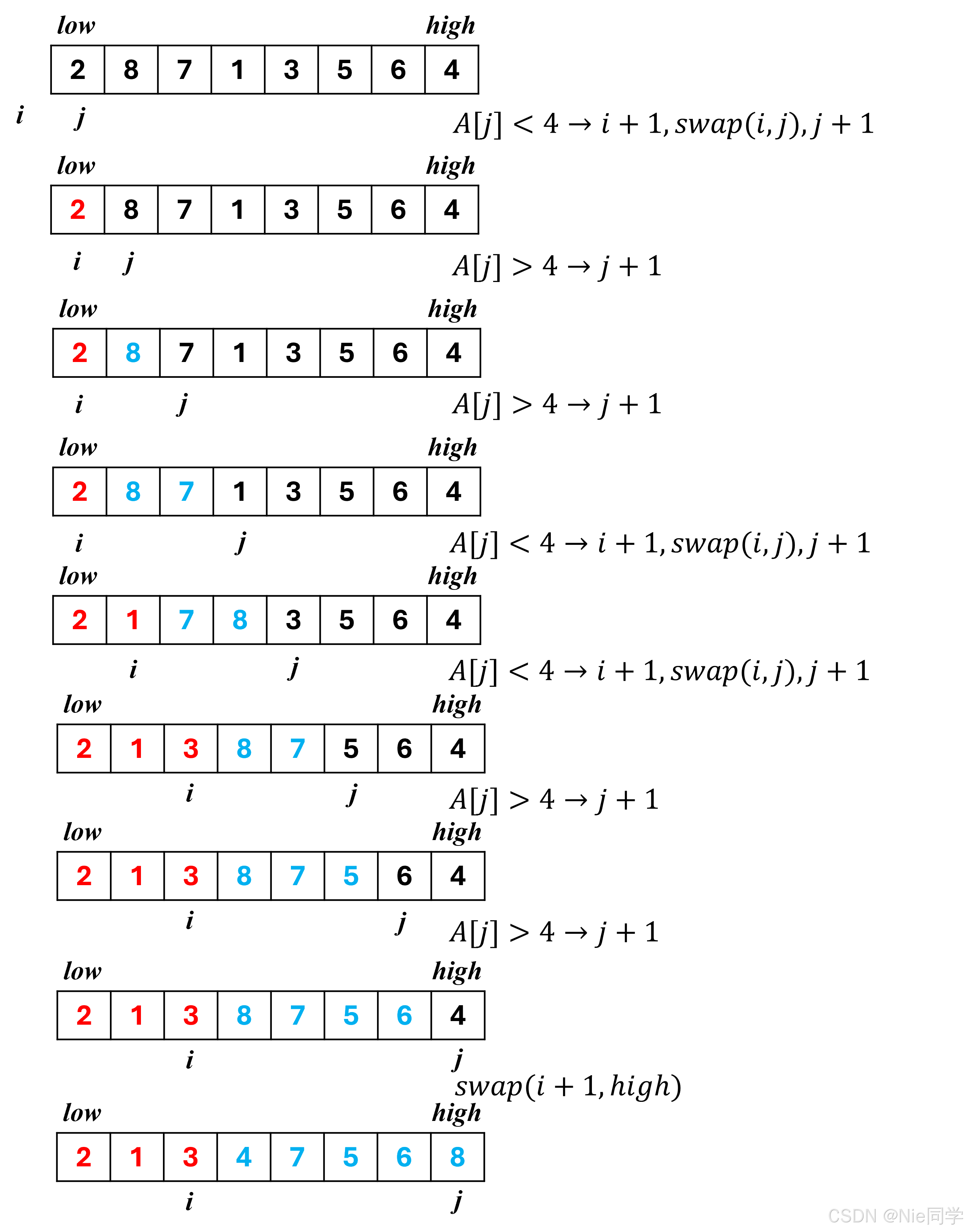
void quickSort(int &A[], int low, int high)
{
		if (low >= high) return;
		
		int mid = partition(A, low, high);

		quickSort(A, low, mid - 1);
		quickSort(A, mid + 1, high);
}

int partition(int &A[], int low, int high)
{
		int i = low - 1, j = low;
		int x = A[high];

		while (j <= high - 1)
		{
				if (A[j] < x) swap(A[ ++ i], A[j]);
				j ++ ;
		}

		swap(A[i + 1], A[high]);
		
		return i + 1;
}

时间复杂度：$O(n{\log }_{2}n)$

假设 $n=2^h$ 且 $T(1)=O(1)$，$T(n)$ 是执行一次大小为 $n$ 次的 quickSort 所需的时间。

• quickSort(A, low, mid - 1)：$T(\frac{n}{2})$
• quickSort(A, mid + 1, high)：$T(\frac{n}{2})$
• int mid = partition(A, low, high)：$O(n)$

$$\begin{array}{rl}T(n)& =2T(\frac{n}{2})+O(n)\\ & \le 2T(\frac{n}{2})+cn\\ & \le 2\left[2T(\frac{n}{2^2})+c\frac{n}{2}\right]+cn\\ & =2^{2}T(\frac{n}{2^2})+2cn\\ & \le ...\\ & =2^{h}T(\frac{n}{2^h})+hcn\\ & =nT(1)+cn{\log }_{2}n\\ & =O(n{\log }_{2}n)\end{array}$$