2020年1月4日 GCD&LCM与快速幂取模
林大OJ 1077 最大公约数与最小公倍数
模板题,背就完事了。
#include <bits/stdc++.h>
using namespace std;
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
int Lcm(int a,int b){
return a/gcd(a,b)*b;
}
int main()
{
int a,b;
while(cin>>a>>b){
cout<<gcd(a,b)<<" "<<Lcm(a,b)<<endl;
}
return 0;
}
也可以直接使用C++中的内置gcd函数,使用方法为__gcd(a,b):
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a,b;
while(cin>>a>>b)
printf("%lld %lld\n",__gcd(a,b),a/__gcd(a,b)*b);
return 0;
}
林大OJ 992 又见GCD
#include <bits/stdc++.h>
using namespace std;
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
int main()
{
int a,b,c,i;
while(cin>>a>>b){
for(i=b+1;;i++){//a一定大于b,所以可以从b+1开始遍历,节省时间
if(gcd(a,i)==b && i!=b){
c=i;
break;
}
}
cout<<c<<endl;
}
return 0;
}
林大OJ 764 多个数的最大公约数
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
long long gcd(long long a,long long b){
return b?gcd(b,a%b):a;
}
int main()
{
long long n,a[11],i;
while(cin>>n){
for(i=1;i<=n;i++)
cin>>a[i];
for(i=1;i<=n-1;i++)
a[i+1]=gcd(a[i],a[i+1]);
printf("%lld\n",a[n]);
}
return 0;
}
林大OJ 765 多个数的最小公倍数
#include <bits/stdc++.h>
using namespace std;
long long gcd(long long a,long long b){
if(b==0) return a;
else return gcd(b,a%b);
}
long long Lcm(long long a,long long b){
return a/gcd(a,b)*b;
}
int main()
{
long long n,a[11],i;
while(cin>>n){
for(i=1;i<=n;i++)
cin>>a[i];
for(i=1;i<=n-1;i++)
a[i+1]=Lcm(a[i],a[i+1]);
cout<<a[n]<<endl;
}
return 0;
}
林大OJ 1221 人见人爱gcd
这道题我只想打他。。
这题要用数学公式推导出gcd(x,y)=gcd(a,b)
从而得到 x² + y² = a²-2 * b * gcd(a,b)

#include <bits/stdc++.h>
using namespace std;
long long gcd(long long a,long long b){
if(b==0) return a;
else return gcd(b,a%b);
}
long long Lcm(long long a,long long b){
return a/gcd(a,b)*b;
}
int main()
{
int t,i;
long long a,b;
while(~scanf("%d",&t)){
while(t--){
scanf("%lld %lld",&a,&b);
printf("%d\n",a*a-2*b*gcd(a,b));
}
}
return 0;
}
林大OJ 1411 LCM&GCD
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){
if(b==0) return a;
else return gcd(b,a%b);
}
ll Lcm(ll a,ll b){
return a/gcd(a,b)*b;
}
int main()
{
ios::sync_with_stdio(false);
ll t,x,i,k,y;
int ans;
while(cin>>t){
while(t--){
ans=0;
cin>>x>>y;//假设gcd(k,i)=x,lcm(k,i)=y,则可得:gcd*lcm=k*i,即x*y=k*i
for(i=x;i<=y;i+=x){//在[x,y]区间内暴力遍历所有i的取值,每次+x(比每次+1要快)
//每次+x的原因是,由于x是k和i的最大公约数,则i一定是x的倍数,所以只需+x即可
if((x*y)%i==0){//满足k*i=x*y,则k=x*y/i,首先必须满足(x*y)%i==0
k=(x*y)/i;//直接得到k的取值
if(Lcm(k,i)==y &&gcd(k,i)==x)//k在[x,y]范围内,并且gcd(k,i)==x,即满足条件
ans++;
}
}
cout<<ans<<endl;
}
}
return 0;
}
林大OJ 1669 高木同学的因子
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){
return b?gcd(b,a%b):a;
}
int main()
{
ios::sync_with_stdio(false);
ll x,y,i;
int ans=0;
cin>>x>>y;
ll k=gcd(x,y);
for(i=1;i*i<k;i++){
if(k%i==0)
ans+=2;
}
if(i*i==k) ans++;
cout<<ans<<endl;
return 0;
}
林大OJ 601 快速幂取模
模板题,重在理解。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll quickmod(ll a,ll b,ll c){
int ret=1;
while(b){
if(b&1)
ret=ret*a%c;
a=a*a%c;
b/=2;
}
return ret;
}
int main()
{
ll a,b,c;
while(cin>>a>>b>>c){
cout<<quickmod(a,b,c)<<endl;
}
return 0;
}
★林大OJ 1666 库特的数学题
终于做出来一道库特题了!
方法1:打表递推。
打表找规律,可以发现 a[n]=6*3(n-1),用快速幂求解即可。方法来源于大佬的题解。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,mod=1e9+7;
ll quickmod(ll a,ll b)
{
ll s=1;
while(b)
{
if(b&1)s=s*a%mod;
a=a*a%mod;b=b/2;
}
return s;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n;
printf("%lld\n",6*quickmod(3,n-1)%mod);//注意算出3的n-1次幂,再乘以6之后一定还要再取模!
return 0;
}
方法2:矩阵快速幂。
方法来源:九度OJ 1081 递推数列。
将求递推数列的第n项转化为求矩阵的n-1次幂,并用快速幂缩短运算时间。
很不幸,超时了。以上算法的时间复杂度为O(k), 当k很大时,会TLE。
再次分析题目,会发现递推公式
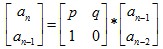
进而推出
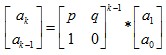
问题转化为求
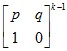
然后用快速幂求解。
#include <bits/stdc++.h>
using namespace std;
#define mod 1000000007
/*将矩阵p与矩阵q相乘,结果存入p矩阵*/
void Matrix_mul(long long p[2][2],long long q[2][2]){
int i,j,k;
long long t[2][2]={0};
for(i=0;i<=1;i++)
for(j=0;j<=1;j++)
for(k=0;k<=1;k++)
t[i][j]+=p[i][k]*q[k][j];
for(i=0;i<=1;i++)
for(j=0;j<=1;j++)
p[i][j]=t[i][j]%mod;
}
/*计算p矩阵的n次方,结果存入p矩阵*/
void Matrix_cal(long long p[2][2],long long n){
int i,j;
long long t[2][2];
for(i=0;i<=1;i++)
for(j=0;j<=1;j++)
t[i][j]=p[i][j];
if(n==1) return;
else if(n&1){
Matrix_cal(p,n-1);
Matrix_mul(p,t);
}
else{
Matrix_cal(p,n/2);
Matrix_mul(p,p);
}
}
int main()
{
long long n;
while(~scanf("%lld",&n))
{
if(n==1)
printf("%d\n",6);
else if(n==2)
printf("%d\n",18);
else
{
long long matrix[2][2]={{2,3},{1,0}};
Matrix_cal(matrix,n-2);//计算从1开始的第n项,总共乘了n-2个中间矩阵
printf("%lld\n",((18*matrix[0][0]%mod)%mod+(6*matrix[0][1]%mod)%mod)%mod);
}
}
return 0;
}
林大OJ 1834 异或方程解的个数
移项n=(n⊕x)+x(⊕表示异或)
可以发现若a的某个二进制位为1,x有2种取值;若a的某个二进制位为0,x有1种取值。
所以只需要计算出a的二进制中1的个数,假设为n,答案就是2^n。
(不用快速幂也行,每次找到n中二进制位为1的地方就直接乘2即可)
先移项:a=x+(a^x),然后看二进制数的某一位,讨论即可发现规律:
a x+(a^x)
1 0+(1^0)==1
1 1+(1^1)==1
0 0+(0^0)==0
0 1+(0^1)==10
可以发现,第四种情况(a==0,x==1)会改变产生进位,改变了a的值,所以排除第四种情况。
综合第三,四种情况,可以发现,如果a的某一位为0的话,那么x对应位只能为0。
再来看第一,第二种情况,我们发现,当a的某一位为1时,x的对应位可以为1,可以为0。
所以,我们只需求出a的二进制数中,有多少个1即可,答案即为2^n
#include <bits/stdc++.h>
using namespace std;
int pre[35],a,k,sum;
int main()
{
pre[0]=1;
for(int i=1;i<=30;i++)
pre[i]=2*pre[i-1];
while(cin>>a){
for(int i=1;i<=30;i++)
if(pre[i]>a){
k=i-1;
break;
}
sum=0;
for(int i=0;i<=k;i++){
if((1<<i)&a)
sum++;
}
cout<<pre[sum]<<endl;
}
return 0;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








