
电力系统故障与计算是电力工程中非常重要的一个方面,涉及到对电力系统中各种故障情形的分析、计算和解决方案设计。通过对电力系统故障的分析,可以确保电力系统在发生故障时的稳定性,并优化电力系统的运行。以下是一些核心概念和计算方法的详细介绍。
电力系统故障分析
电力系统故障是指在电力系统运行过程中,由于设备故障或外部因素的影响,系统某部分出现的电气异常现象。这些故障可能是由于设备损坏、导线短路、过载等多种因素引起的。常见的电力系统故障类型包括:
-
短路故障:包括单相接地短路、两相短路、两相接地短路、三相短路等。
- 单相接地故障:发生在一相与地之间,导致电力系统中性点电压波动。
- 两相短路:发生在两相之间,通常比单相接地故障更加严重。
- 三相短路:是最严重的故障类型,通常涉及到三相电力系统中的所有相。
-
开路故障:当电力系统的某一部分线路或设备发生开路时,会导致电流无法流通,电力供应中断。
-
过载故障:设备负荷过大,超过额定工作范围,导致电气设备损坏或失效。
电力系统故障计算
故障计算是对电力系统故障状态下的电流、电压、功率等进行的分析和计算,以便评估故障对系统稳定性的影响,并制定相应的处理措施。常见的故障计算方法包括:
-
对称分量法(Symmetrical Components Method)
- 对称分量法是解决不对称故障(例如单相接地、两相短路等)的经典方法。通过将不对称的故障分解为三个对称的分量:正序分量、负序分量和零序分量,简化了故障分析的过程。
- 正序分量:代表正常运行的电力系统状态,三相电流和电压对称。
- 负序分量:反映了不对称负载或故障的影响,通常出现在故障状态下。
- 零序分量:代表由零序电流和电压产生的不对称故障,通常与地面接触有关。
-
故障电流计算:
- 故障电流的大小和特性对于电力系统的保护和设备选择至关重要。在计算故障电流时,通常需要考虑到系统的短路容量、线路阻抗以及设备的阻抗等因素。
- 短路电流计算涉及到使用变压器的等效模型、线路的阻抗矩阵等数据,来求解系统在不同故障条件下的电流分布。
-
稳定性分析:
- 故障发生后,电力系统的稳定性需要特别关注,特别是在故障发生后是否能迅速恢复供电。稳定性分析常包括暂态稳定性分析和小扰动稳定性分析。
-
保护设备配置与选择:
- 为了保护电力系统的设备和人员安全,电力系统故障分析的结果会用于配置合理的保护设备,包括过电流保护、差动保护、距离保护等。
- 保护设备需要根据故障电流大小、故障类型和系统的运行特性来选择和调整。
故障分析的应用
-
提高系统可靠性:通过故障分析,可以设计合理的电力系统保护策略,防止由于故障引发的大规模停电事故。
-
设备选型:故障电流计算帮助确定适当的设备容量和保护设置,确保电力系统的设备能够承受故障电流并及时切断故障部分。
-
故障隔离与恢复:在发生故障时,通过对故障位置和类型的准确分析,可以快速实现故障隔离和电力恢复,保证系统的持续运行。
-
优化系统设计:根据故障分析结果,可以优化电力系统的设计,例如调整变电站的布局、优化线路选择和负荷分配。
结语
电力系统故障分析与计算是保障电力系统稳定、可靠运行的重要手段。通过深入的故障分析、有效的故障计算和合理的保护措施,可以大大提升电力系统的安全性与经济性。

这张图列出了一些非常关键的关于电力系统故障分析与对称分量法的问题,下面我来逐条进行详细讲解:
1. 三相不对称故障如何分析计算?
三相不对称故障包括:
- 单相接地故障(最常见)
- 两相短路
- 两相接地
- 三相不等幅不等角短路等
分析方法:
- 使用对称分量法:将不对称电流和电压分解为正序、负序、零序分量;
- 构建三个序网络(正序、负序、零序网络);
- 在故障点将三个网络按不同方式连接(并联、串联),再进行等值电路分析;
- 利用变换矩阵将序电流、电压转化为相量形式。
2. 正序、负序、零序加在对称系统上有什么特点?
在一个理想对称的三相系统中:
- 正序分量:电压或电流的三相大小相等,间隔120°,与原系统方向一致;
- 负序分量:大小相等,120°相位差,但方向相反;
- 零序分量:三相电压或电流大小相等、相位相同(无相差),通常只在系统不平衡或与地有关的故障中存在。
特点总结:
- 对称运行时,只有正序分量存在;
- 不对称运行时(如故障或不平衡负载),会出现负序和零序;
- 这三类序分量在系统中分别通过对应序网络传输。
3. 对称分量法?
定义:
对称分量法是将任意三相不对称系统变量(电压、电流)分解为三个对称系统分量的方法。
数学表达:
如果 ( A ), ( B ), ( C ) 是三相电流,则:
[
\begin{bmatrix} I_0 \ I_1 \ I_2 \end{bmatrix} = \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \ 1 & a & a^2 \ 1 & a^2 & a \end{bmatrix} \begin{bmatrix} I_A \ I_B \ I_C \end{bmatrix}
]
其中:
- ( I_0 ): 零序分量
- ( I_1 ): 正序分量
- ( I_2 ): 负序分量
- ( a = e{j120\circ} ):120°复数旋转因子
该方法使得复杂的不对称问题转换为三个对称问题来分别处理,大大简化计算。
4. 中性点的阻抗对正序、负序、零序有什么影响?
- 正序电流:一般与中性点无关,不通过中性线;
- 负序电流:同样也不通过中性线,主要与负载不平衡有关;
- 零序电流:必须通过中性点或大地,因此中性点的阻抗会直接影响零序网络。
举例:
- 如果中性点接地电阻较大,则零序电流受限制;
- 如果中性点不接地(或阻抗很大),则零序电流近似为0,系统对接地故障的响应变弱。
5. 变压器的零序等值电路如何确定?
变压器在零序状态下的行为不同于正负序,主要取决于其绕组接线方式:
- Y接地-Y接地:零序可通过,零序阻抗为两侧零序阻抗之和;
- Y不接地-Δ:零序电流无法传递;
- Δ-Y接地:零序电流无法通过Δ侧,但Δ绕组会有环流,影响计算;
- 零序网络的建模要根据接线方式判断是否连通以及阻抗大小。
常规步骤:
- 查图纸确定接线方式;
- 判断零序电流是否能流通;
- 给出等值电路中是否存在阻抗支路,以及其数值;
- 与其他设备组成完整零序网络。

现在详细讲一下电力系统中的不对称短路故障,这是继对称三相短路之后更具实际意义的分析内容,因为现实系统中大多数故障其实都是不对称的。
🌩 什么是不对称短路?
在三相电力系统中,正常运行或三相短路时各相对称。但如果故障只发生在部分相(如一相或两相),则系统将进入不对称状态,称为不对称故障或不对称短路。
这些故障电压和电流在幅值和相位上都不再对称,常见的不对称故障包括:
| 故障类型 | 描述 | 发生概率 | 特点 |
|---|---|---|---|
| 单相接地故障 | 一相(如A)对地短路 | 最常见 | 存在零序电流 |
| 两相短路(无接地) | 两相(如BC)相间短路 | 较常见 | 无零序分量 |
| 两相接地短路 | 两相(如BC)同时接地短路 | 一般 | 有零序分量 |
| 三相不对称短路 | 三相不等幅不等相位的短路(少见) | 极少 | 最复杂 |
🧠 为什么需要特别分析?
不对称故障会引起:
- 电动机产生负序电流 → 产生转矩波动 → 机械震荡甚至烧毁;
- 系统电压跌落严重;
- 保护装置误动作或拒动;
- 零序电流可能导致接地网、电缆屏蔽层烧毁;
🧮 如何分析不对称故障?
分析这类故障的标准方法是——对称分量法(Symmetrical Components Method)。
🔁 第一步:三相量 → 对称分量变换
将不对称的三相量分解为三个对称分量:
[
\begin{bmatrix}
I_0 \
I_1 \
I_2
\end{bmatrix}
= \frac{1}{3}
\begin{bmatrix}
1 & 1 & 1 \
1 & a & a^2 \
1 & a^2 & a
\end{bmatrix}
\begin{bmatrix}
I_a \
I_b \
I_c
\end{bmatrix}
]
其中:
- ( I_0 ):零序分量
- ( I_1 ):正序分量
- ( I_2 ):负序分量
- ( a = e{j120\circ} )
🔄 第二步:构建三序网络
将系统模型拆成三个独立网络:
- 正序网络:表示正常运行的系统阻抗(电源、电感等);
- 负序网络:表示不对称扰动的等效阻抗;
- 零序网络:考虑接地阻抗、变压器接线等因素。
不同故障类型,连接方式不同:
| 故障类型 | 三序网络连接方式(串/并) |
|---|---|
| 单相接地 | 零、负、正 序串联 |
| 两相短路 | 负、正 序串联 |
| 两相接地 | 零、负、正 序串联 |
| 三相短路 | 仅正序网络参与 |
📌 第三步:计算故障电流、电压
- 写出序电流电压的KVL/KCL方程;
- 解方程得到序分量值;
- 用逆变换还原出三相电流和电压。
🧾 示例:A相接地短路
设电源内阻抗为:
- 正序阻抗:( Z_1 )
- 负序阻抗:( Z_2 )
- 零序阻抗:( Z_0 )
故障点接地电阻为 ( R_f )
序网络连接如下(串联):
[
I_0 = I_1 = I_2 = \frac{E}{Z_0 + Z_1 + Z_2 + 3R_f}
]
计算出序电流后,再变换回三相电流。
🔌 不对称故障与设备影响
| 序分量 | 对设备的影响 |
|---|---|
| 正序 | 正常运行电流,无危害 |
| 负序 | 产生电机转矩波动、振动、发热 |
| 零序 | 流经接地网、电缆金属层 → 发热甚至烧毁 |
🛡 保护策略
- 负序电流保护:检测电机或变压器的非正常负载;
- 零序电压/电流保护:用于接地故障检测;
- 距离保护、差动保护等配合使用,提升故障识别精度。
✅ 总结
| 项目 | 三相对称故障 | 不对称故障(单相、两相) |
|---|---|---|
| 分析复杂度 | 简单 | 高 |
| 使用网络 | 只用正序网络 | 用三序网络 |
| 影响 | 对称,冲击性大 | 不对称,负序零序影响严重 |
| 应对策略 | 快速切断、自动重合闸 | 细致检测、分量保护、接地方案 |
如果你想,我还可以:
- 演示一个具体的不对称短路计算;
- 画出对应的序网络连接图;
- 模拟故障点电流波形变化;
- 或解释某设备(如变压器)在某类故障下的响应。

对称分量法(Symmetrical Components Method)展开深入讲解——这是分析电力系统中不对称故障(尤其是单相、两相短路等)最重要的数学工具之一,也是电力系统保护和稳定分析的基础方法。
🔍 一、什么是对称分量法?
对称分量法由美国电机工程师 Fortescue 于1918年提出,其核心思想是:
“任何不对称的三相系统,都可以分解成三个对称的分量系统:正序分量、负序分量和零序分量。”
这样做的好处是:将复杂的不对称问题变成了三个对称问题分别分析,大大简化了计算!
⚡️ 二、三种序分量的定义与特性
设三相电压(或电流)分别为:
[
V_a,\quad V_b,\quad V_c
]
则对应的序分量为:
-
零序分量(Zero-sequence component)
所有三相分量幅值相同,相位一致
[
V_0 = \frac{1}{3}(V_a + V_b + V_c)
] -
正序分量(Positive-sequence component)
三相大小相等,相位相差120°,相序与正常系统一致
[
V_1 = \frac{1}{3}(V_a + a V_b + a^2 V_c)
] -
负序分量(Negative-sequence component)
与正序相反的旋转方向,相位仍相差120°
[
V_2 = \frac{1}{3}(V_a + a^2 V_b + a V_c)
]
其中 ( a = e{j120\circ} = -\frac{1}{2} + j\frac{\sqrt{3}}{2} )
🧮 三、数学形式(变换矩阵)
✅ 三相 → 三序(正变换):
[
\begin{bmatrix}
V_0 \
V_1 \
V_2
\end{bmatrix}
= \frac{1}{3}
\begin{bmatrix}
1 & 1 & 1 \
1 & a & a^2 \
1 & a^2 & a
\end{bmatrix}
\begin{bmatrix}
V_a \
V_b \
V_c
\end{bmatrix}
]
✅ 三序 → 三相(逆变换):
[
\begin{bmatrix}
V_a \
V_b \
V_c
\end{bmatrix}
\begin{bmatrix}
1 & 1 & 1 \
1 & a^2 & a \
1 & a & a^2
\end{bmatrix}
\begin{bmatrix}
V_0 \
V_1 \
V_2
\end{bmatrix}
]
这意味着,只要知道三序分量,就能还原三相值。
🧰 四、对称分量法的实际应用步骤
💡 场景:单相接地故障(A相接地)
步骤如下:
- 识别故障类型与位置;
- 将系统中三相电压电流分解为三序分量;
- 构建三个序网络(零序、正序、负序);
- 根据故障类型将三序网络串联或并联连接;
- 求解序电流/电压;
- 使用逆变换还原回三相电压或电流;
- 分析故障影响、制定保护动作方案。
📊 五、序网络连接规律(重点!)
| 故障类型 | 序网络连接方式 | 特点说明 |
|---|---|---|
| 单相接地 | 零序、负序、正序串联 | 存在零序分量,受接地阻抗影响大 |
| 两相短路 | 负序、正序串联 | 无零序分量 |
| 两相接地 | 零序、负序、正序串联 | 两相同时接地,零序回路形成 |
| 三相短路 | 仅用正序网络 | 电流最大,对称 |
🛠 六、对称分量法的典型应用
- 故障分析(特别是不对称故障);
- 保护整定(负序保护、零序电流保护等);
- 设备运行监测(监测负序电流是否过高);
- 仿真模拟(如PSCAD/EMTDC, DIgSILENT, Matlab Simulink);
- 中性点接地方案设计(影响零序回路);
📌 七、实际意义与工程价值
| 应用场景 | 序分量的意义 |
|---|---|
| 变压器运行 | 零序分量判断中性点接地情况 |
| 电机保护 | 负序电流过大 → 负序保护动作 |
| 中性点故障检测 | 零序电流出现或突变 → 判断单相接地故障 |
| 波形监测 | 通过DFT提取序分量 → 实现在线监测与自动化判断 |
✅ 总结精要
| 分量类型 | 特征 | 存在条件 | 主要作用 |
|---|---|---|---|
| 正序 | 正常三相对称旋转 | 所有故障类型 | 反映系统主电源供电能力 |
| 负序 | 反方向旋转,三相不对称 | 不对称故障 | 电机过热、负序保护等 |
| 零序 | 三相同幅同相 | 接地故障 | 接地保护、判断中性点状态 |
如果你感兴趣,我可以进一步给出:
- 一个完整的数值计算案例(比如单相接地求故障电流);
- 一个变压器零序网络构建示例;
- 或者 Matlab/手算推导一组对称变换过程。

这张图展示的是在分析不对称短路故障时使用的一个非常重要的理论工具——电路等值原理,尤其强调了如何用**戴维南等值(Thevenin Equivalent)**来处理不对称电压加在系统中的求解问题。
🔧 一、电路等值原理简介
电路等值原理的本质是:
将一个复杂电力系统中非故障部分 用一个电压源 + 等值阻抗代替,只保留影响故障点的部分。
这个原理的好处是:
- 极大简化了计算;
- 保留对故障电流、电压的主要影响因素;
- 是故障分析中的基础技巧。
⚡ 二、图中逻辑解释
👉 结构划分:
图中分为三部分:
- 正常电力系统部分(左侧):即未发生故障的部分;
- 故障电压源(右上):由于三相不对称,产生了不对称电压源;
- 故障部分(右下):短路位置、接地电阻、电弧等建模组成;
它们之间的连接方式:
- 故障电压源施加在正常系统上;
- 用戴维南等值电路替代正常系统,即一个电压源 ( \bar{E}{th} ) + 一个阻抗 ( Z{th} );
- 最终问题简化为一个单一故障回路分析问题。
🧠 三、图中重点术语解释
🔺 三相电压不对称
故障时三相电压幅值、相位不一致,导致系统非平衡。这是对称分量法存在的前提。
🔁 戴维南等值
戴维南定理指出:
一个任意线性网络,在任意两个端口之间,可以等效为一个 电压源 + 阻抗 的串联结构。
在电力系统中:
- 该电压源是正序电压(通常为系统母线电压);
- 该阻抗为系统的序阻抗(正序、负序、零序等);
- 这就是我们常说的“系统等值电源”。
🛠 四、求解思路总结(配合对称分量法)
这张图其实暗示了 不对称故障求解的三步策略:
| 步骤 | 操作 | 工具 |
|---|---|---|
| 1️⃣ | 将系统划分为“非故障部分 + 故障部分” | 电路等值原理 |
| 2️⃣ | 将非故障部分戴维南等值 | 戴维南定理 |
| 3️⃣ | 将三相电压不对称 → 三序电压 | 对称分量法 |
✍️ 举个例子:A相接地短路
- 将系统划分:变压器、线路、电源 → 非故障部分;
- 对A相接地点做戴维南等值:
- ( E_1 ):正序戴维南电压;
- ( Z_1, Z_2, Z_0 ):正、负、零序戴维南阻抗;
- 将A相故障建模为:三序电压串联,求故障电流。
📘 结尾总结
| 核心概念 | 作用 |
|---|---|
| 电路等值原理 | 简化系统结构 |
| 戴维南等值 | 替代复杂网络,保留本质影响 |
| 三相电压不对称 | 引出序分量分析的必要性 |
| 对称分量法 | 将不对称问题 → 三个对称问题分别分析 |
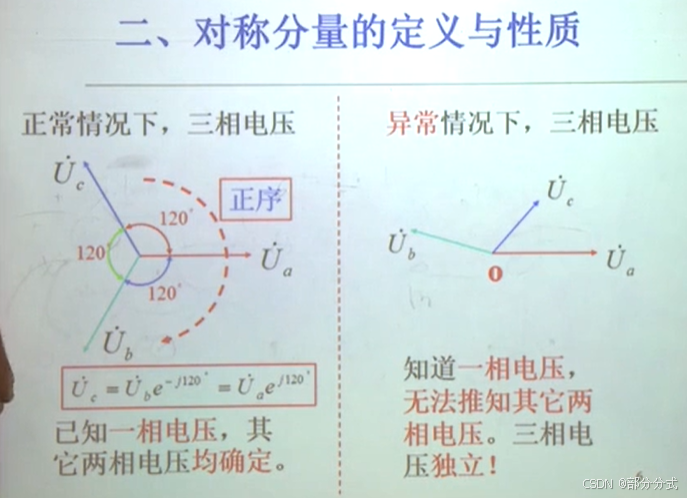
这张图非常清晰地解释了对称分量的定义与性质,特别是对正常与异常(三相对称与不对称)情况的电压分布特性做了对比。我们逐点来详细讲解👇
🔷 一、标题:《对称分量的定义与性质》
对称分量的核心就是:
将三相电压/电流(不管是否对称)分解为 正序、负序、零序 三部分。
🟢 左边:正常情况下(三相电压对称)
特性:
- 三相电压幅值相等,彼此之间相差120°;
- 是标准的“正序分量”形式;
- 在这种情况下,只要知道任意一相电压,可以推导出其余两相!
图中表示:
- 电压向量 ( \vec{U}_a, \vec{U}_b, \vec{U}_c ) 形成一个120°的三相旋转;
- 它们遵循公式:
[
\vec{U}_b = \vec{U}_a e{-j120\circ},\quad \vec{U}_c = \vec{U}_a e{j120\circ}
] - 在对称系统中,这种旋转规律严格成立,三相联动。
📌 结论:
知道一相电压即可唯一确定整个三相电压系统。
🔴 右边:异常情况下(三相电压不对称)
特性:
- 电压幅值和相位不再相等;
- 三相之间不再存在严格的120°角度关系;
- 系统进入非对称状态,这正是我们说的“不对称电压”。
图中表示:
- 三个电压向量散乱、方向不一;
- 显然彼此无固定相位差,不能再用“旋转因子”推导出其他相。
📌 结论:
只知道一相电压,无法确定其余两相,三相电压是独立变量。
✅ 核心对比总结
| 情况 | 特点 | 变量关系 | 分析方法 |
|---|---|---|---|
| 正常(三相对称) | 大小相等,相差120° | 一相推三相 | 单相等效或正序分析 |
| 异常(不对称) | 幅值、相位各不相同 | 三相独立 | 对称分量法(三序网络) |
🧠 所以为何要用对称分量法?
因为当三相电压/电流不对称时,传统三相分析法失效!必须使用对称分量法来将其拆解为可处理的“对称部分”分析。
📚 补充知识:对称分量的三种成分再回顾一下
| 分量 | 相位关系 | 意义 | 是否存在于对称运行中 |
|---|---|---|---|
| 正序 | 120°,方向正常 | 正常运行电压/电流 | ✅ 是 |
| 负序 | 120°,方向反向 | 表征不平衡分量 | ❌ 否 |
| 零序 | 同相、同幅值 | 地故障/不平衡电流 | ❌ 否 |
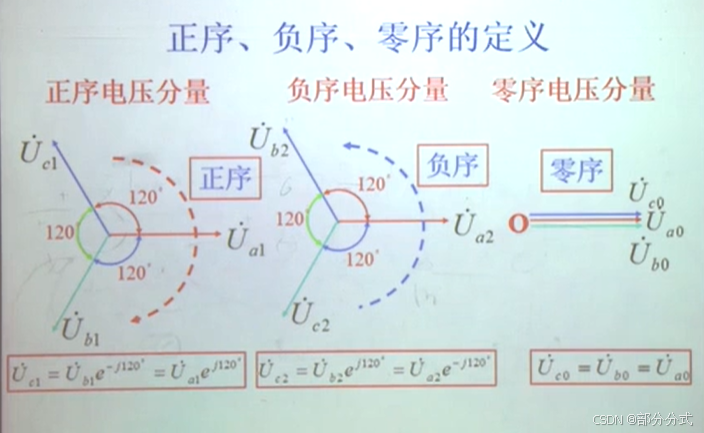
这张图深入讲解了正序、负序、零序电压分量的定义,并展示了它们在三相系统中的具体表现。图中通过三种不同的电压分量来说明对称分量的概念。我们来逐步解析每一部分。
🔴 正序电压分量
特性:
- 正序电压表示正常对称的三相电压系统,三相电压大小相等、相位相差120°;
- 在图中,正序电压的向量(如 ( \vec{U}_1 ), ( \vec{U}_2 ), ( \vec{U}_3 ))形成一个完整的旋转电压向量,通常为正常系统的电压。
数学表达:
- 正序电压分量:
[
\vec{U}{c1} = \vec{U}{b1} e{-j120\circ} = \vec{U}_{a1} e{j120\circ}
] - 它们在空间中围绕原点旋转,相位差为120°,并且遵循旋转公式。
🟢 负序电压分量
特性:
- 负序电压表示不对称三相系统中不对称部分的电压,三相电压大小相等、相位相差120°,但是方向相反于正序电压;
- 负序电压是故障或不平衡负载等情况下的电压分量,通常出现在不对称故障中。
数学表达:
- 负序电压分量:
[
\vec{U}{c2} = \vec{U}{b2} e{-j120\circ} = \vec{U}_{a2} e{j120\circ}
] - 它的旋转方向与正序电压相反,代表了系统的不平衡部分。
🔵 零序电压分量
特性:
- 零序电压表示三相电压大小相等且相位一致的情况,通常与接地故障、系统不平衡以及其他一些特定情况相关;
- 在图中,零序电压分量表现为三相电压相位相同,大小相等。
数学表达:
- 零序电压分量:
[
\vec{U}{c0} = \vec{U}{b0} = \vec{U}_{a0}
] - 它们的相位完全一致,通常与地故障等不平衡情况有关。
🧠 核心要点总结:
- 正序电压:代表正常、对称运行的三相系统,三相电压大小相等,相位相差120°;
- 负序电压:代表不对称或不平衡故障(如单相接地、两相短路等),三相电压大小相等,相位差120°,方向反向;
- 零序电压:代表三相电压幅值相等、相位相同的情况,通常与接地故障相关。
💡 应用:
在电力系统中,对称分量法使用这三种分量来将复杂的不对称故障分解为多个对称系统进行分析,从而简化问题并进行有效计算。

这张图内容非常关键,是对对称分量法理论基础的数理证明部分,来自于经典的**“对称分量定理”**。我们逐条分析它所表达的内容:
📘 标题:定理 1
任意一组三相电压,均可唯一分解为:
- 正序分量(第一列)
- 负序分量(第二列)
- 零序分量(第三列)
这个定理是对称分量法的数学基础,也就是说:
所有不对称三相电压,都可以通过对称分量变换,写成三个独立子系统的向量和。
✅ 公式表达:
[
\begin{bmatrix}
\vec{U}_a \
\vec{U}_b \
\vec{U}_c
\end{bmatrix}
\begin{bmatrix}
\vec{U}{a1} \
\vec{U}{b1} \
\vec{U}{c1}
\end{bmatrix}
+
\begin{bmatrix}
\vec{U}{a2} \
\vec{U}{b2} \
\vec{U}{c2}
\end{bmatrix}
+
\begin{bmatrix}
\vec{U}{a0} \
\vec{U}{b0} \
\vec{U}_{c0}
\end{bmatrix}
]
其中:
- 下标“1”:正序;
- 下标“2”:负序;
- 下标“0”:零序。
🧮 变换基础 —— “旋转因子 a”
[
a = e{j120\circ} = -\frac{1}{2} + j\frac{\sqrt{3}}{2},\quad a^2 = e{-j120\circ} = -\frac{1}{2} - j\frac{\sqrt{3}}{2}
]
这些是对称分量法中最基础的复数单位旋转因子,具有如下特性:
- ( a^3 = 1 )
- ( 1 + a + a^2 = 0 )
🧠 推导逻辑梳理(底部部分)
在这个证明中:
- 利用旋转因子的特性,将三相电压用对称关系表示;
- 例如:
[
\vec{U}{b1} = a^2 \vec{U}{a1},\quad \vec{U}{c1} = a \vec{U}{a1}
]
表示正序三相电压的相位关系; - 同样的,负序分量的关系则为:
[
\vec{U}{b2} = a \vec{U}{a2},\quad \vec{U}{c2} = a^2 \vec{U}{a2}
] - 零序则三相相等:
[
\vec{U}{a0} = \vec{U}{b0} = \vec{U}_{c0}
]
🧾 所以我们可以总结如下:
🔺 对称分量展开公式(核心):
[
\begin{bmatrix}
\vec{U}_a \
\vec{U}_b \
\vec{U}_c
\end{bmatrix}
\underbrace{
\begin{bmatrix}
1 & 1 & 1 \
1 & a^2 & a \
1 & a & a^2
\end{bmatrix}
}_{\text{对称分量逆变换矩阵}}
\cdot
\begin{bmatrix}
\vec{U}_0 \
\vec{U}_1 \
\vec{U}_2
\end{bmatrix}
]
这是从三序分量 → 三相量的变换公式。
📌 工程意义
| 项目 | 作用 |
|---|---|
| 正序分量 | 表示系统正常运行部分电压/电流 |
| 负序分量 | 表示系统不平衡部分,对电机有破坏作用 |
| 零序分量 | 表示接地或中性点不平衡引起的共同模式变化 |


































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








