子串
560.和为K的子数组【没理解】

什么是前缀和:前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身)
通常,会在前缀和首位放一个0。比如数组[1,2,3。其前缀和是[0,1,3,6]
前缀和通常可以帮助我们快速计算某个区间内的和。
比如我们要算i,j之间的和,那么就是nums[i]+nums[i+1]+⋯+nums[j]=前缀和(j) - 前缀和(i-1)
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
presum = 0
record = {0:1}
res = 0
for i in range(len(nums)):
presum += nums[i]
r = presum - k
if r in record:
res += record[r]
record[presum] = record.get(presum, 0) + 1
return res
该方法超时
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
# 要求的连续子数组
count = 0
n = len(nums)
preSum = [0]
# 求前缀和数组,第i位置代表nums前面i个相加,共有len(nums)+1长
tmp = 0
for i in range(n):
tmp += nums[i]
preSum.append(tmp)
# 求和为k的连续子数组,求i到j之间的和
for i in range(1, n+1):
for j in range(i, n+1):
if preSum[j] - preSum[i-1] == k: # preSum[j] - preSum[i-1]代表着在nums数组中,前j个数之和减去前i-1个数之和
count += 1
return count
【暴力解法】
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
# 要求的连续子数组
count = 0
n = len(nums)
for i in range(n):
sum = 0
for j in range(i, n):
sum += nums[j]
if sum == k:
count += 1
return count
239.滑动窗口最大值【大顶堆】

from collections import deque
class MyQueue: #单调队列(从大到小
def __init__(self):
self.queue = deque() #这里需要使用deque实现单调队列,直接使用list会超时
#每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
#同时pop之前判断队列当前是否为空。
def pop(self, value):
if self.queue and value == self.queue[0]:
self.queue.popleft()#list.pop()时间复杂度为O(n),这里需要使用collections.deque()
#如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
#这样就保持了队列里的数值是单调从大到小的了。
def push(self, value):
while self.queue and value > self.queue[-1]:
self.queue.pop()
self.queue.append(value)
#查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
def front(self):
return self.queue[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
result = []
for i in range(k): #先将前k的元素放进队列
que.push(nums[i])
result.append(que.front()) #result 记录前k的元素的最大值
for i in range(k, len(nums)):
que.pop(nums[i - k]) #滑动窗口移除最前面元素
que.push(nums[i]) #滑动窗口前加入最后面的元素
result.append(que.front()) #记录对应的最大值
return result
76.最小覆盖子串【双指针|滑动窗口】【困难】

- 用need字典维护,当前还需要的字符以及个数,need[i]为负数,代表无需求,need[i]代表需要
- 滑动串口,先让right动起来,左指针指向队首,如果能cover字符T;就开始收缩窗口,让left滑动,直至不能coverT
- 在窗口滑动过程中,维护的need也要变,加入字符,就–,减去字符就+
class Solution:
def minWindow(self, s: str, t: str) -> str:
ans_left, ans_right = -1, len(s)
left = 0
cnt_s = Counter() # s 子串字母的出现次数
cnt_t = Counter(t) # t 中字母的出现次数
for right, c in enumerate(s): # 移动子串右端点
cnt_s[c] += 1 # 右端点字母移入子串
while cnt_s >= cnt_t: # 涵盖【收集结果】
if right - left < ans_right - ans_left: # 找到更短的子串
ans_left, ans_right = left, right # 记录此时的左右端点
cnt_s[s[left]] -= 1 # 左端点字母移出子串
left += 1 # 移动子串左端点
return "" if ans_left < 0 else s[ans_left: ans_right + 1]
如果尝试访问一个在 defaultdict 中不存在的键,它会自动创建一个新键,并将其值设置为默认值(在这个例子中是 0)。但是{}不支持自动创建键
def minWindow(self, s: str, t: str) -> str:
need=collections.defaultdict(int)
for c in t:
need[c]+=1
needCnt=len(t)
left=0
res=(0,float('inf'))
for index,c in enumerate(s):
if need[c]>0: #如果需要字母c
needCnt-=1
need[c]-=1
if needCnt==0: #步骤一:滑动窗口包含了所有T元素
while True: #步骤二:增加left,排除多余元素
c=s[left]
if need[c]==0:
break
need[c]+=1
left+=1
if index-left<res[1]-res[0]: #记录结果,当前窗口左指针left,右指针index
res=(left,index)
need[s[left]]+=1 #步骤三:left增加一个位置,寻找新的满足条件滑动窗口
needCnt+=1
left+=1
return '' if res[1]>len(s) else s[res[0]:res[1]+1] #如果res始终没被更新过,代表无满足条件的结果
普通数组
53.最大子数组和【动态规划】

因为dp[i]只与dp[i-1]和nums[i]有关,因此直接在nums原地修改,空间复杂度O(1)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
for i in range(1,len(nums)):
nums[i] = max(nums[i-1]+nums[i],nums[i])
return max(nums)
'''
dp[i]:以nums[i]结尾的连续子数组的,最大和
dp[i] = max(dp[i-1]+nums[i], nums[i])
dp[0]=nums[0]
'''
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [0] * len(nums)
dp[0] = nums[0]
for i in range(1, len(nums)):
dp[i] = max(dp[i-1]+nums[i], nums[i])
return max(dp)
56.合并区间

- 先对左节点排序
- 判断当前合并区间和候选区间,是否重叠
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
ans = []
intervals.sort() # 按照所有区间的左端点进行排序
for interval in intervals:
if not ans or ans[-1][1] < interval[0]: #当ans为空,或者 当前区间的右节点 在 候选区间的左边【无重叠】
ans.append(interval)
else: #当前并区间和候选区间 有重叠
ans[-1][1] = max(interval[1],ans[-1][1]) #取最大右区间
return ans
189.轮转数组

直接用nums会报错??
修改nums[:]不会影响到nums,nums[;]是一个新列表,是nums的副本,她两指向不同内存地址
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
k = k % len(nums)
nums[:] = nums[len(nums)-k:] + nums[:len(nums)-k]
return nums
238.除自身以外数组的乘积

- 先初始化ans,ans[0]=1;辅助变量temp=1
- 计算下三角,计算上三角乘积temp,并乘以上三角
索引容易搞错,可以看个图,根据图写索引
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
ans = [1] * len(nums)
temp = 1
for i in range(1,len(nums)):
ans[i] = ans[i-1] * nums[i-1] #下三角
for j in range(len(nums)-2,-1,-1):
temp *= nums[j+1] #上三角
ans[j] *= temp #下三角 * 上三角
return ans
41.缺失的第一个正数【困难】
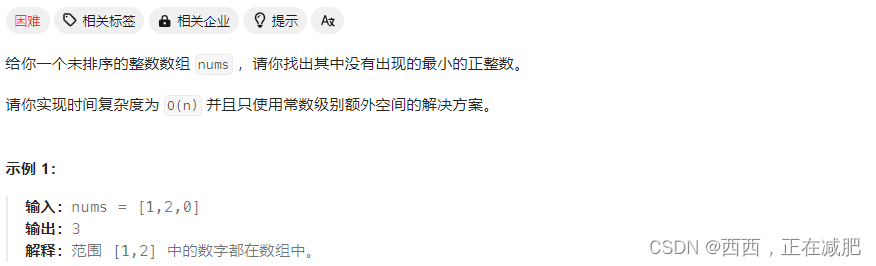
最后的结果一定是在 [1,n+1] 内
修改 nums,使对应的下标 [0,n] 里 nums[i] 第一个不是 i+1 的,i+1 就是答案
也就是,让 nums 里的数字,在 [1,n] 内的,都去他们对应的 [0,n-1] 位置上去的
'''
1.把数字【1,n】放到nums上,nums[i]=i+1
2.遍历nums,如果nums[i] !=i+1,代表缺失
'''
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
n = len(nums)
for i in range(n):
while 1 <= nums[i] <= n and nums[nums[i] - 1] != nums[i]:
# 这是错误的
# nums[i], nums[nums[i] - 1] = nums[nums[i] - 1], nums[i]
#先计算右边的值,也就是nums[i]和nums[nums[i] - 1]的值,然后将他们赋值给一个临时元祖;
#然后按顺序赋值给左边,也就是说会先修改nums[i]的值,这样一来,nums[i] - 1就不是原来想要修改的下标了。
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
for i in range(n):
if nums[i] != i + 1:
return i + 1
return n + 1
矩阵
73.矩阵置0

两遍扫matrix,第一遍用集合记录哪些行,哪些列有0;第二遍置0
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
row = len(matrix)
col = len(matrix[0])
row_zero = set()
col_zero = set()
for i in range(row):
for j in range(col):
if matrix[i][j] == 0:
row_zero.add(i)
col_zero.add(j)
for i in range(row):
for j in range(col):
if i in row_zero or j in col_zero:
matrix[i][j] = 0
54.螺旋矩阵
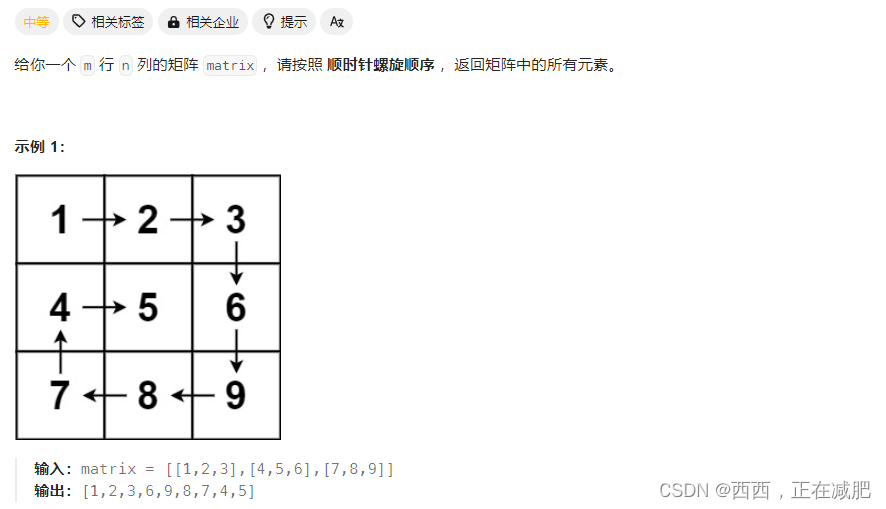
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix: return []
left, right, top, bottom = 0, len(matrix[0]) - 1, 0, len(matrix) - 1
res = []
while True:
for i in range(left, right + 1):
res.append(matrix[top][i]) #从左上角 到 右上角
top += 1
if top > bottom:
break
for i in range(top, bottom + 1):
res.append(matrix[i][right]) # 从右上角 到 右下角
right -= 1
if left > right:
break
for i in range(right, left - 1, -1):
res.append(matrix[bottom][i]) # 从右下角 到左下角
bottom -= 1
if top > bottom:
break
for i in range(bottom, top - 1, -1):
res.append(matrix[i][left]) #从左下角 到 左上角
left += 1
if left > right:
break
return res
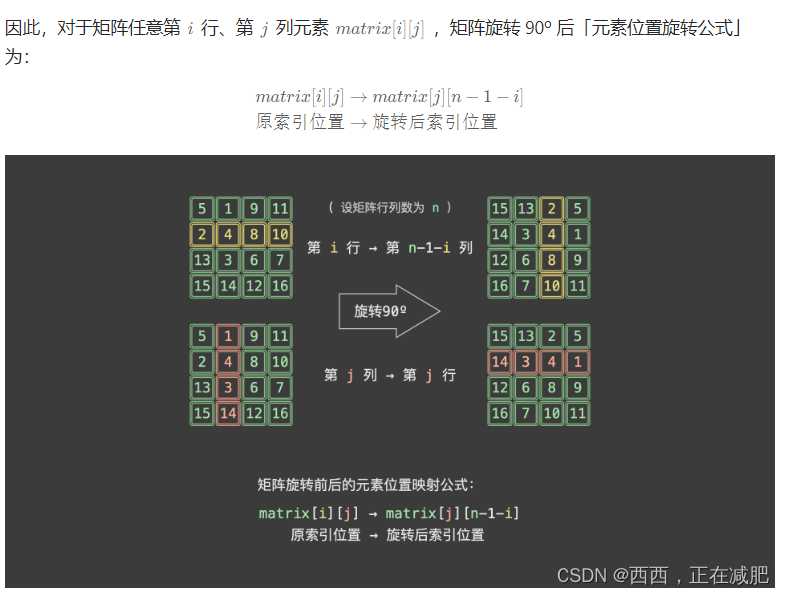
48.旋转图像

方法一:借助一个辅助矩阵temp暂存原矩阵
方法二:原地修改。一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 1/41/41/4 的各元素为起始点执行以上旋转操作,即可完整实现矩阵旋转。【当矩阵大小n为偶数,就取n//2行,n//2列原始为起始点;矩阵大小n为奇数,取前n//2行,(n+1)//2列为起始点
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
temp = copy.deepcopy(matrix) # 深拷贝 matrix -> tmp
for i in range(n):
for j in range(n):
matrix[i][j] = temp[n-j-1][i] # 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
for i in range(n//2):
for j in range((n+1)//2):
temp = matrix[i][j]
matrix[i][j] = matrix[n-j-1][i]
matrix[n-j-1][i] = matrix[n-i-1][n-j-1]
matrix[n-i-1][n-j-1] = matrix[j][n-i-1]
matrix[j][n-i-1] = temp
240.搜索二维矩阵||

'''
起点为右上角,向左走:变小,向右走:变大
'''
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
i, j = 0, len(matrix[0])-1
while i<len(matrix) and j >= 0:
if matrix[i][j] > target:
j -= 1
elif matrix[i][j] < target:
i += 1
else:
return True
return False





























 657
657

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








