1. 奇偶校验码
> 校验码
校验码是指能够发现或能够自动纠正错误的数据编码,也称检错纠错码。
校验码的原理是通过增加一些冗余码,来检验或纠错编码。

如上图,添加一位冗余码,这时当出现位错误时(如 100 -> 101),就会发现变为非法状态进而检错。
> 几个概念
- 码字: 由若干位代码组成的一个字
- 码字间的距离:两个码字逐位对比,具有不同位的个数
- 码距:各合法码字间的最小距离
当码距 d = 1 时,无检错能力;d >= 2 时,有检错能力。码距越大,检错、纠错能力越强。
> 奇偶校验码
- 奇校验码:整个校验码(有效信息位和校验位)中 1 的个数为奇数
- 偶校验码:整个校验码(有效信息位和校验位)中 1 的个数为偶数
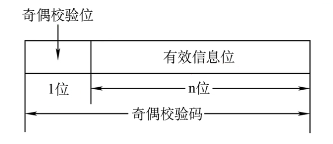
具体来说如何检验这就涉及到计网所学:

> 偶检验的硬件实现
各信息进行异或运算,得到的结果即为偶校验位:

2. 海明校验码
海明码实际上是一种多重奇偶校验码。其实现原理是将信息位分组进行奇偶校验,有多个校验位,并且多个校验位可以标注出出错位置。
> 确定校验位数目
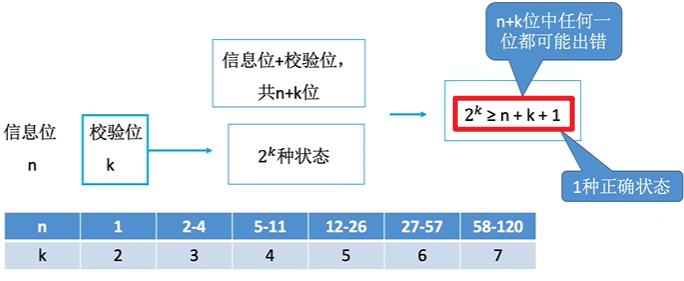
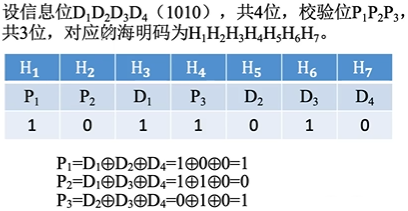
设信息位为 D 4 D 3 D 2 D 1 D_4D_3D_2D_1 D4D3D2D1 共 4 位,则校验位 P 3 P 2 P 1 P_3P_2P_1 P3P2P1 共 3 位,对应海明码 H 7 H 6 H 5 H 4 H 3 H 2 H 1 H_7H_6H_5H_4H_3H_2H_1 H7H6H5H4H3H2H1 。
> 确定校验位的分布
海明码规定,校验位 P i P_i Pi 要放在海明位号为 2 i − 1 2^{i-1} 2i−1 的位置上。因此, H 1 H_1 H1 = P 1 P_1 P1、 H 2 H_2 H2 = P 2 P_2 P2、 H 4 H_4 H4 = P 3 P_3 P3
对于信息位
D
4
D
3
D
2
D
1
D_4D_3D_2D_1
D4D3D2D1 (1010),按顺序插入,则有:

> 校验位的值
将每个信息位所处的海明位号以二进制形式表示出来,校验位
P
i
P_i
Pi 的值为第 i 组(由该校验位校验的数据位)所有位求异或,如下图:

则有下表:

> 海明的校验原理
每个校验组分布利用校验位和参与形成该校验位的信息位进行奇偶校验,构成 k 个校验方程:
- S 1 = P 1 ⊕ D 1 ⊕ D 2 ⊕ D 4 S_1 = P_1 ⊕ D_1 ⊕ D_2 ⊕ D_4 S1=P1⊕D1⊕D2⊕D4
- S 2 = P 2 ⊕ D 1 ⊕ D 3 ⊕ D 4 S_2 = P_2 ⊕ D_1 ⊕ D_3 ⊕ D_4 S2=P2⊕D1⊕D3⊕D4
- S 3 = P 3 ⊕ D 2 ⊕ D 3 ⊕ D 4 S_3 = P_3 ⊕ D_2 ⊕ D_3 ⊕ D_4 S3=P3⊕D2⊕D3⊕D4
若
S
3
S
2
S
1
S_3S_2S_1
S3S2S1 值为
000
000
000 ,则说明没有出错;否则说明出错,
S
3
S
2
S
1
S_3S_2S_1
S3S2S1 即为错误位位号。具体来说:

注意:有的题目可能信息位和校验位顺序是颠倒的,如 D 1 D 2 D 3 D 4 D_1D_2D_3D_4 D1D2D3D4、 P 1 P 2 P 3 P_1P_2P_3 P1P2P3,但是其做法是不变的,只不过调整顺序即可。
> 补充
海明码具有 1 个比特位的纠错能力,和 2 个比特位的检错能力。但是它无法区分到底是 1 位错误还是 2 位错误。
为了解决此问题,海明码使用时通常在首部加上 全校验位 ,对整体进行偶校验。

S
3
S
2
S
1
=
000
S_3S_2S_1 = 000
S3S2S1=000 且全体偶校验成功,则没有出错。
S
3
S
2
S
1
≠
000
S_3S_2S_1 ≠ 000
S3S2S1=000 且全体偶校验失败,则有 1 位出错,纠错即可。
S
3
S
2
S
1
≠
000
S_3S_2S_1 ≠ 000
S3S2S1=000 且全体偶校验成功,则有 2 位出错,需要重传。
ps:不得不说,海明太强了,怪不得获得了图灵奖
3. 循环冗余校验码
> 基本思想
收发双方约定好一个 生成多项式 G(x) ,发送方基于待发送的数据和生成多项式计算出 R 位校验码 ,将其添加到 K 位信息码 (待传输数据)的后面一起传输。

在接收端,利用生成多项式对接收到的 K+R 位 CRC 码 进行模 2 除法,若整除则说明没有出错,否则要进行重传或纠错。
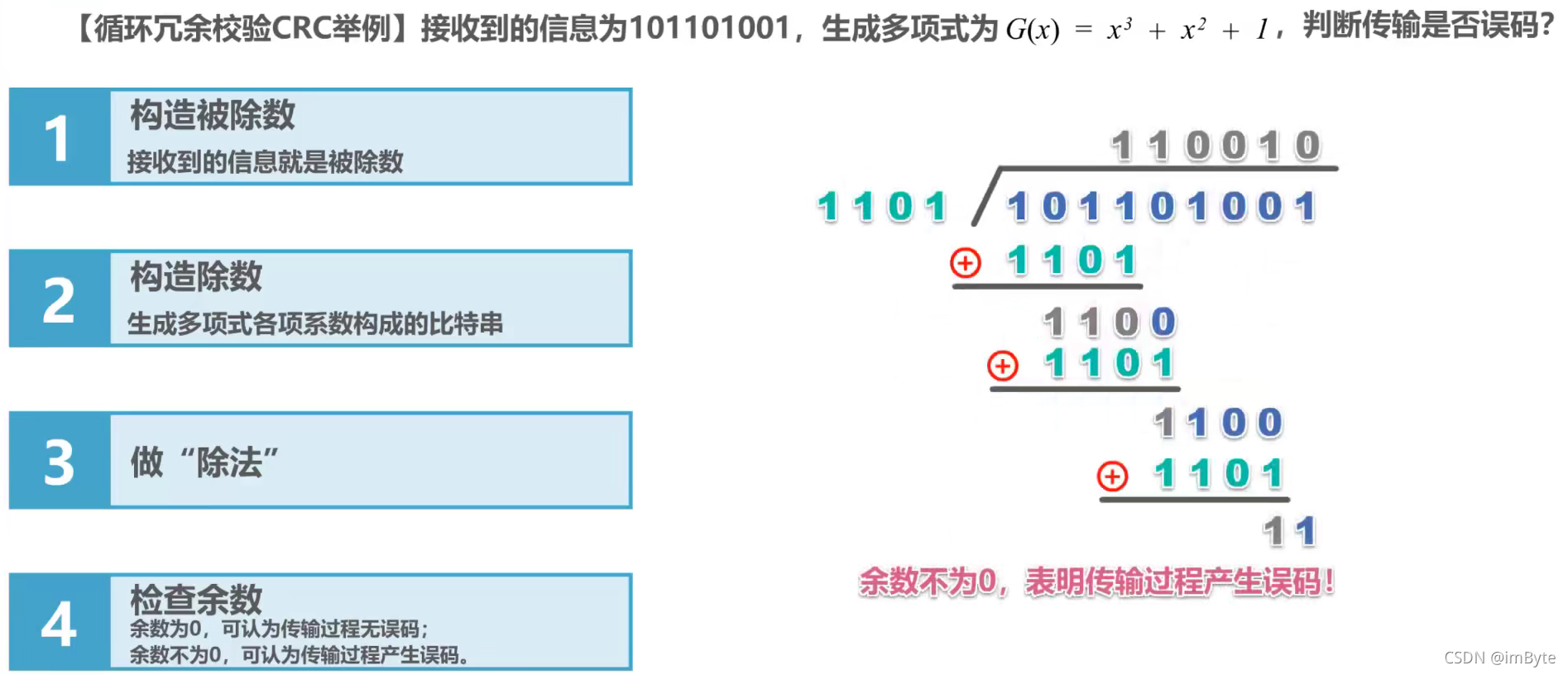
> 具体来说
首先,计算出 R 位校验码,即下图所示余数,并拼接成 K + R 位 CRC 码发送给接收端:

之后,对接收收到的信息与生成多项式系数所构成的比特串相除,看余数是否为 0 :
> 检错和纠错
对于上述例子,出错位置和对应余数如下图所示:
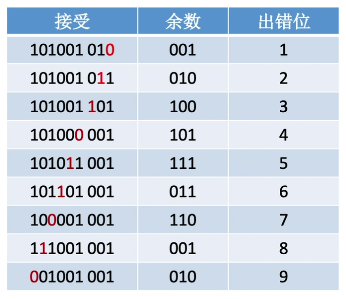
可以看出,即使计算出余数为 010 并不一定是第二位出错,也可能是第九位出错。
上图是从王道考研视频中扒下来的,其实从第二行开始数据就错了。用在这里只是想说明一下 CRC 码是否可以纠错与 R 的位数是相关的,如果能够一一对应,CRC 码是可以纠错的,只需取反即可。
其实,若生成多项式选择得当,满足 2^R ≥ K+R+1,则 CRC 码是可以纠正 1 位错误的。但一般在差错检测是信息位远大于检错位,所以循环冗余校验实际中只用来检错。










 本文详细介绍了几种常见的校验码,包括奇偶校验码、海明校验码和循环冗余校验码的工作原理和应用。通过对这些校验码的理解,可以帮助读者更好地掌握数据通信中的错误检测与纠正技术。
本文详细介绍了几种常见的校验码,包括奇偶校验码、海明校验码和循环冗余校验码的工作原理和应用。通过对这些校验码的理解,可以帮助读者更好地掌握数据通信中的错误检测与纠正技术。

















 2122
2122

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










