二叉树

二叉树的基本概念

二叉树(binary tree,简写成BT)是一种特殊的树型结构，它的度数为2的树。即二叉树的每个结点最多有两个子结点。每个结点的子结点分别称为左孩子、右孩子，它的两棵子树分别称为左子树、右子树。二叉树有5中基本形态：

 前面引入的树的术语也基本适用于二叉树，但二叉树与树也有很多不同，如：首先二叉树的每个结点至多只能有两个结点，二叉树可以为空，二叉树一定是有序的，通过它的左、右子树关系体现出来。

二叉树的性质

【性质1】在二叉树的第i层上最多有2^{i - 1}个结点(i >= 1)。

证明：很简单，用归纳法：当i = 1时，2^{i - 1} = 1 显然成立；现在假设第 i - 1 层时命题成立，即第i - 1层上最多有 2^{i –2} 个结点。由于二叉树的每个结点的度最多为 2，故在第i层上的最大结点数为第 i - 1层的2倍， 即 2 * 2^{i - 2}=2^{i – 1}。

【性质2】深度为k的二叉树至多有2^k –1个结点(k >= 1)。 证明：在具有相同深度的二叉树中，仅当每一层都含有最大结点数时，其树中结点数最多。因此利用性质1可得，深度为k的二叉树的结点数至多为： 2⁰ + 2¹ + …+ 2^{k - 1} = 2^k - 1 故命题正确。

【特别】

• 一棵深度为k且有2^k–1个结点的二叉树称为满二叉树。如下图A为深度为4的满二叉树，这种树的特点是每层上的结点数都是最大结点数。 可以对满二叉树的结点进行连续编号，约定编号从根结点起，自上而下，从左到右，
• 由此引出完全二叉树的定义，深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树。 下图B就是一个深度为4，结点数为12的完全二叉树。它有如下特征：叶结点只可能在层次最大的两层上出现；对任一结点，若其右分支下的子孙的最大层次为m，则在其左分支下的子孙的最大层次必为m或m+1。下图中C、D不是完全二叉树

【性质3】对任意一棵二叉树，如果其叶结点数为n₀，度为2的结点数为n₂，则一定满足：n₀=n₂+1。 证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)应等于0度结点数n₀、1度结点n₁和2度结点数n₂之和：n=n_o+n₁+n₂ ……(式子1)   另一方面，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是： n₁+2n₂ 树中只有根结点不是任何结点的孩子，故二叉树中的结点总数又可表示为： n=n₁+2n₂+1 ……(式子2) 由式子1和式子2得到： n_o=n₂+1

【性质4】具有n个结点的完全二叉树的深度为floor(log2n)+1 证明：假设深度为k，则根据完全二叉树的定义，前面k-1层一定是满的，所以n>2k –1 -1。但n又要满足n<=2k -1。所以，2k–1–1<n<=2k -1。变换一下为2k–1<=n<2k。 以2为底取对数得到：k-1<=log2n<k。而k是整数，所以k= floor(log2n)+1。

【性质5】对于一棵n个结点的完全二叉树，对任一个结点(编号为i)，有： ①如果i=1,则结点i为根，无父结点；如果i>1,则其父结点编号为i/2。 如果2*i>n，则结点i无左孩子(当然也无右孩子，为什么？即结点i为叶结点)；否则左孩子编号为2*i。 ②如果2*i+1>n，则结点i无右孩子；否则右孩子编号为2*i+1。

证明：略，我们只要验证一下即可。总结如图：

特殊二叉树

一、满二叉树

　　一棵二叉树的结点要么是叶子结点，要么它有两个子结点(如果一个二叉树的层数为K，且结点总数是(2^k) -1，则它就是满二叉树。)

二、完全二叉树

　　若设二叉树的深度为k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，第k 层所有的结点都连续集中在最左边，这就是完全二叉树。

三、平衡二叉树

　　它或者是一颗空树，或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

四、最优二叉树(哈夫曼树)

　　树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

二叉树的存储结构

链式存储结构

——即单链表结构或双链表结构(同树)。数据结构修改如下：

typedef struct node;
typedef node *tree;
struct node　
{
    char data;
    tree lchild, rchild;
    　　
};
tree bt;

或

typedef struct node;
typedef node *tree;
struct node
{
    char data;
    tree lchild, rchild, father;
    　　
};
tree bt;

如左图的一棵二叉树用单链表就可以表示成右边的形式：

顺序存储结构

——几个数组加一个指针变量。数据结构修改如下：

const int n = 10;
char data[n];
char lchild[n];
char rchild[n];
int bt; //根结点指针

二叉树在处理表达式时经常用到，一般用叶结点表示运算元，分支结点表示运算符。这样的二叉树称为表达式树。如现在有一个表达式：(a+b/c)*(d-e)。可以用以图表示：

数据结构定义如下：

按表达式的书写顺序逐个编号，分别为1..9，注意表达式中的所有括号在树中是不出现的，因为表达式树本身就是有序的。叶结点的左右子树均为空(用0表示)。 　　

char data[9] = {'a', '+', 'b', '/', 'c', '*', 'd', '-', 'e'};
int lchild[9] = {0,1,0,3,0,2,0,7,0};
int rchild[9] = {0,4,0,5,0,8,0,9,0};
int bt; //根结点指针,初值=6，指向'*'

二叉树的操作: 最重要的是遍历二叉树，但基础是建一棵二叉树、插入一个结点到二叉树中、删除结点或子树等。

例3 医院设置

【问题描述】 设有一棵二叉树(如图3-8，其中圈中的数字表示结点中居民的人口，圈边上数字表示结点编号。现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻结点之间的距离为1。就本图而言，若医院建在1处，则距离和=4+12+2*20+2*40=136；若医院建在3处，则距离和=4*2+13+20+40=81……

【输入格式】 输入文件名为hospital.in，其中第一行一个整数n，表示树的结点数(n<=100)。接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格(一个或多个)分隔，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接，为0表示无链接。

【输出格式】 输出文件名为hospital.out，该文件只有一个整数，表示最小距离和。

 【样例输入】

5 　　

13 2 3 　　

4 0 0 　　

12 4 5 　　

20 0 0 　　

40 0 0

【样例输出】 　　

81

【算法分析】 这是一道简单的二叉树应用问题，问题中的结点数并不多，数据规模也不大，采用邻接矩阵存储，用Floyed法求出任意两结点之间的最短路径长，然后穷举医院可能建立的n个结点位置，找出一个最小距离的位置即可。当然也可以用双链表结构或带父结点信息的数组存储结构来解决，但实际操作稍微麻烦了一点。

【参考程序】

#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
int a[101];
int g[101][101];
int main()
{
    int n, i, j, k, l, r, min, total;
    freopen("hospital.in", "r", stdin);
    freopen("hospital.out", "w", stdout);
    cin >> n;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            g[i][j] = 1000000;
    for (i = 1; i <= n; i++) //读入、初始化
    {
        g[i][i] = 0;
        cin >> a[i] >> l >> r;
        if (l > 0)
            g[i][l] = g[l][i] = 1;
        if (r > 0)
            g[i][r] = g[r][i] = 1;
    }
    for (k = 1; k <= n; k++) //用Floyed求任意两结点之间的最短路径
        for (i = 1; i <= n; i++)
            if (i != k)
                for (j = 1; j <= n; j++)
                    if (i != j && k != j && g[i][k] + g[k][j] < g[i][j])
                        g[i][j] = g[i][k] + g[k][j];
    min = 0x7fffffff;
    for (i = 1; i <= n; i++) //穷举医院建在N个结点，找出最短距离
    {
        total = 0;
        for (j = 1; j <= n; j++)
            total += g[i][j] * a[j];
        if (total < min)
            min = total;
    }
    cout << min << endl;
    return 0;
}

二叉树的遍历

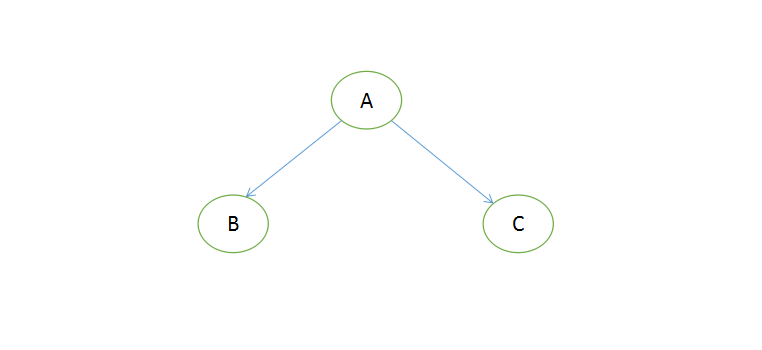
二叉树遍历分为三种：前序、中序、后序，其中序遍历最为重要。为啥叫这个名字？是根据根节点的顺序命名的。

比如上图正常的一个满节点，A：根节点、B：左节点、C：右节点，前序顺序是ABC(根节点排最先，然后同级先左后右)；中序顺序是BAC(先左后根最后右)；后序顺序是BCA(先左后右最后根)。

    

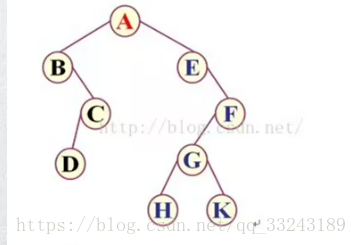
比如上图二叉树遍历结果

    前序遍历：ABCDEFGHK

    中序遍历：BDCAEHGKF

    后序遍历：DCBHKGFEA

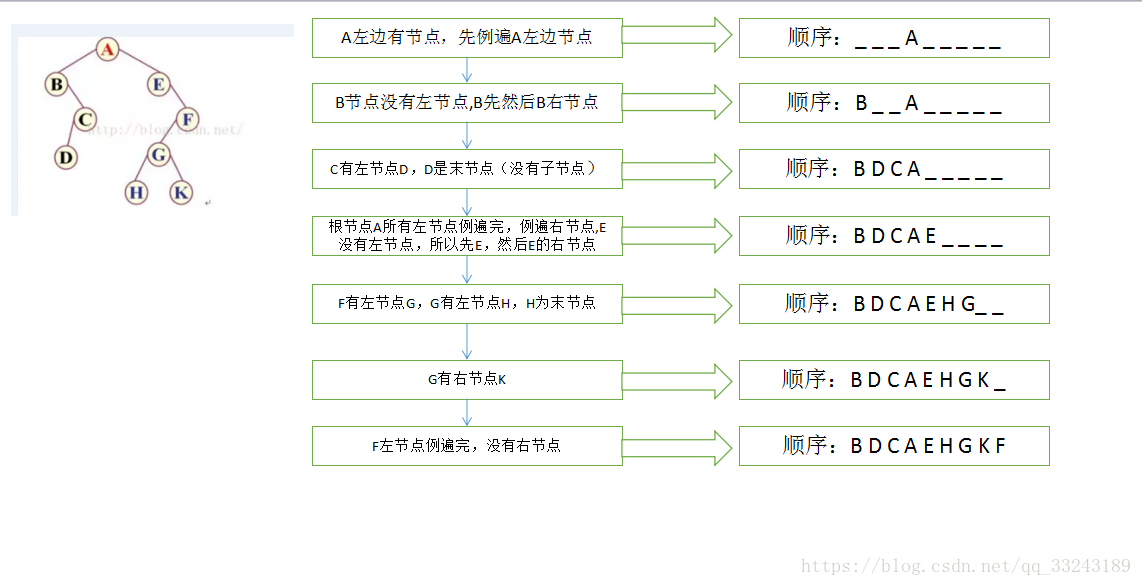
分析中序遍历如下图，中序比较重要(java很多树排序是基于中序，后面讲解分析)

前序遍历

对于当前节点，先输出该节点，然后输出他的左孩子，最后输出他的右孩子。以上图为例，递归的过程如下：
(1)：输出 1，接着左孩子；
(2)：输出 2，接着左孩子；
(3)：输出 4，左孩子为空，再接着右孩子；
(4)：输出 6，左孩子为空，再接着右孩子；
(5)：输出 7，左右孩子都为空，此时 2 的左子树全部输出，2 的右子树为空，此时 1 的左子树全部输出，接着 1 的右子树；
(6)：输出 3，接着左孩子；
(7)：输出 5，左右孩子为空，此时 3 的左子树全部输出，3 的右子树为空，至此 1 的右子树全部输出，结束。

中序遍历

对于当前结点，先输出它的左孩子，然后输出该结点，最后输出它的右孩子。以上图为例：
(1)：1-->2-->4，4 的左孩子为空，输出 4，接着右孩子；
(2)：6 的左孩子为空，输出 6，接着右孩子；
(3)：7 的左孩子为空，输出 7，右孩子也为空，此时 2 的左子树全部输出，输出 2，2 的右孩子为空，此时 1 的左子树全部输出，输出 1，接着 1 的右孩子；
(4)：3-->5，5 左孩子为空，输出 5，右孩子也为空，此时 3 的左子树全部输出，而 3 的右孩子为空，至此 1 的右子树全部输出，结束。

后序遍历

对于当前结点，先输出它的左孩子，然后输出它的右孩子，最后输出该结点。依旧以上图为例：
(1)：1->2->4->6->7，7 无左孩子，也无右孩子，输出 7，此时 6 无左孩子，而 6 的右子树也全部输出，输出 6，此时 4 无左子树，而 4 的右子树全部输出，输出 4，此时 2 的左子树全部输出，且 2 无右子树，输出 2，此时 1 的左子树全部输出，接着转向右子树；
(2)：3->5，5 无左孩子，也无右孩子，输出 5，此时 3 的左子树全部输出，且 3 无右孩子，输出 3，此时 1 的右子树全部输出，输出 1，结束。

根据前序遍历中序遍历推导树的结构

已知：
前序遍历: GDAFEMHZ
中序遍历: ADEFGHMZ
求后序遍历
首先，要先画出这棵二叉树，怎么画呢？根据上面说的我们一步一步来……
1.先看前序遍历，前序遍历第一个一定是根节点，那么我们可以知道，这棵树的根节点是G，接着，我们看中序遍历中，根节点一定是在中间访问的，那么既然知道了G是根节点，则在中序遍历中找到G的位置，G的左边一定就是这棵树的左子树，G的右边就是这棵树的右子树了。
2.我们根据第一步的分析，大致应该知道左子树节点有：ADEF，右子树的节点有：HMZ。同时，这个也分别是左子树和右子树的中序遍历的序列。
3.在前序遍历遍历完根节点后，接着执行前序遍历左子树，注意，是前序遍历，什么意思？就是把左子树当成一棵独立的树，执行前序遍历，同样先访问左子树的根，由此可以得到，左子树的根是D，第2步我们已经知道左子树是ADEF了，那么在这一步得到左子树的根是D，请看第4步。
4.从第2步得到的中序遍历的节点序列中，找到D，发现D左边只有一个A，说明D的左子树只有一个叶子节点，D的右边呢？我们可以得到D的右子树有EF，再看前序遍历的序列，发现F在前，也就是说，F是先前序遍历访问的，则得到E是F的左子树，只有一个叶子节点。
5.到这里，我们可以得到这棵树的根节点和左子树的结构了。如下图：

6.接着看右子树，在第2步的右子树中序遍历序列中，右子树是HMZ三个节点，那么先看前序遍历的序列，先出现的是M，那么M就是右子树的根节点，刚好，HZ在M的左右，分别是它的左子树和右子树，因此，右子树的结构就出来了：

7.到这里，我们可以得到整棵树的结构：

根据树的中序遍历后序遍历推导树的结构

中序遍历：ADEFGHMZ
后序遍历：AEFDHZMG

1..根据后序遍历的特点(左右中)，根节点在结尾，确定G是根节点。根据中序遍历的特点(左中右)，确定ADEF组成左子树，HMZ组成右子树。

2.分析左子树。ADEF这四个元素在后序遍历(左右中)中的顺序是AEFD，在中序遍历(左中右)中的顺序是ADEF。根据后序遍历(左右中)的特点确定D是左子树的节点，根据中序遍历(左中右)的特点发现A在D前面，所以A是左子树的左叶子，EF则是左子树的右分枝。
EF在后序(左右中)和中序(左中右)的相对位置是一样的，所以EF关系是左右或者左中，排除左右关系(缺乏节点)，所以EF关系是左中。
到此得出左子树的形状

3.分析右子树。HMZ这三个元素在中序遍历(左中右)的顺序是HMZ，在后序遍历(左右中)的顺序是HZM。根据后序遍历(左右中)的特点，M在尾部，即M是右子树的节点。再根据中序遍历(左中右)的特点，确定H(M的前面)是右子树的左叶子，Z(M的后面)是右子树的右叶子。

所以右子树的形状

4.最后得出整棵树的形状

例题：下落的树叶

输入格式

输出格式 

#include <iostream>
#include <cstring>
using namespace std;
#define maxn 10010
int sum[maxn];
void build(int p)
{
    int v;
    cin >> v;
    if (v == -1)
    {
        return;
    }
    sum[p] += v;
    build(p - 1);
    build(p + 1);
}

bool init()
{
    int v;
    cin >> v;
    if (v == -1)
    {
        return false;
    }
    memset(sum, 0, sizeof(sum));
    int pos = maxn / 2;
    sum[pos] = v;
    build(pos - 1);
    build(pos + 1);
    return true;
}

int main()
{
    int kase = 0;
    while (init())
    {
        int p = 0;
        while (sum[p] == 0)
            p++;
        cout << "Case " << ++kase << "：\n"
             << sum[p++];
        while (sum[p] != 0)
        {
            cout << " " << sum[p++];
        }
        cout << "\n\n";
    }
    return 0;
}