第六题、图的广度优先搜索（难度系数100）

图的广度优先搜索
描述：
图的广度优先搜索类似于树的按层次遍历，即从某个结点开始，先访问该结点，然后访问该结点的所有邻接点，再依次访问各邻接点的邻接点。如此进行下去，直到所有的结点都访问为止。在该题中，假定所有的结点以“A”–“Z”中的若干字符表示，且要求结点的访问顺序要求根据由“A”至“Z”的字典顺序进行访问。例如有如下图：

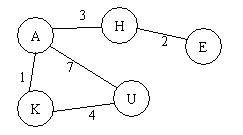
如果要求从H开始进行广度优先搜索，则搜索结果为：H->A->E->K->U.
输入：
输入只包含一个测试用例，第一行为一个自然数n，表示顶点的个数，第二行为n个大写字母构成的字符串，表示顶点，接下来是为一个n*n大小的矩阵，表示图的邻接关系。数字为0表示不邻接，否则为相应的边的长度。
最后一行为一个字符，表示要求进行广度优先搜索的起始顶点。
输出：
用一行输出广度优先搜索结果，起始点为给定的顶点，各顶点之间用一个空格隔开。要求同一顶点的邻接点的访问顺序按“A”—“Z”的字典顺序。
样例输入：

5
HUEAK
0 0 2 3 0
0 0 0 7 4
2 0 0 0 0
3 7 0 0 1
0 4 0 1 0
H

样例输出：

H A E K U

参考：

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        String name = sc.next();
        int[][] mp = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                mp[i][j] = sc.nextInt();
            }
        }
        String be = sc.next();
        int begin = name.indexOf(be);
        boolean[] vis = new boolean[n];
        Queue<Integer> q = new LinkedList<>();
        q.add(begin);
        while (!q.isEmpty()) {
            int fr = q.poll();
            System.out.print(name.charAt(fr) + " ");
            vis[fr] = true;
            ArrayList<Character> al = new ArrayList<>();
            for (int i = n - 1; i >= 0; i--) {
                if (mp[fr][i] != 0 && !vis[i]) {
                    al.add(name.charAt(i));
                    vis[i] = true;
                }
            }
            Collections.sort(al);
            for (int i = 0; i < al.size(); i++) {
                q.add(name.indexOf(al.get(i)));
            }
        }
    }
}