1. 红黑树的优势
- 有了二叉搜索树,为什么还需要平衡二叉树?
二叉搜索树容易退化成一条链,这时,查找的时间复杂度从 O ( l o g 2 N ) O(log_2N) O(log2N) 将退化成 O ( N ) O(N ) O(N),引入对左右子树高度差有限制的平衡二叉树,保证查找操作的最坏时间复杂度也为 O ( l o g 2 N ) O(log_2N) O(log2N) - 有了平衡二叉树,为什么还需要红黑树?
AVL(平衡二叉树)的左右子树高度差不能超过1,每次进行插入/删除操作时,几乎都需要通过旋转操作保持平衡,在频繁进行插入/删除的场景中,频繁的旋转操作使得AVL的性能大打折扣。
红黑树通过牺牲严格的平衡,换取插入/删除时少量的旋转操作,整体性能优于AVL。红黑树插入时的不平衡,不超过两次旋转就可以解决;删除时的不平衡,不超过三次旋转就能解决。通过红黑树的红黑规则,保证最坏的情况下,也能在 O ( l o g 2 N ) O(log_2N) O(log2N)时间内完成查找操作。
2. 红黑规则
- 非黑即红
- 根节点为黑色
- 叶节点为黑色(叶节点是指末梢的空节点Null)
- 一个节点为红色,则其两个子节点必须是黑色的(根到叶子的所有路径,不可能存在两个连续的红色节点)
- 每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度)
3. 左旋转算法
rotateLeft(TreeNode<K,V> root,TreeNode<K,V> p)
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
// 确保 p 的右孩子 r 不为空
if (p != null && (r = p.right) != null) {
// 将 r 上面的 左孩子 覆盖原来 p 上面的右孩子
if ((rl = p.right = r.left) != null)
rl.parent = p;
// 将 r 作为 头节点 与 p 原来父节点相连,若为null说明作为了根,黑色
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
// p 作为了 r 的左孩子
r.left = p;
p.parent = r;
}
return root;
}

4. 右旋转算法
rotateRight(TreeNode<K,V> root,TreeNode<K,V> p)
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
// 确保 p 的 左孩子 l 不为null
if (p != null && (l = p.left) != null) {
// 将 l 上的 右孩子 覆盖 p 的 左孩子
if ((lr = p.left = l.right) != null)
lr.parent = p;
// 将 l 作为头节点 连接 p 原来的父亲,若为null说明作为了根,黑色
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
// p 作为了 l 的右孩子
l.right = p;
p.parent = l;
}
return root;
}
5. 插入平衡算法
规则:
- 插入的节点设为红色
- 若该节点没有父节点,为根节点,黑色
- 若该节点的父亲为黑色或者祖父节点为null,则不用继续调整
- 若该节点的父亲为红色并且祖父节点不为空:
- 判断父节点为祖父的左孩子还是右孩子
- 若叔节点存在并且为红色,则父、叔节点变为黑色,祖父变为红色,祖父视为新的插入节点向上调整
- 若叔节点为空或者叔节点为黑色,则根据父节点在祖父的左边还是右边进行旋转,上色规则为叔父都变为黑色,祖父变为红色,以祖父为旋转p点(前后黑色高度不变)
balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x)
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// 新插入的节点设为红色
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
// 如果 x的父节点 为空
// 说明 x节点 为根节点-黑色
x.red = false;
return x;
} else if (!xp.red || (xpp = xp.parent) == null)
// 如果 x的父节点 为黑色 || x的祖父节点 为空
// 说明 不需要再调整,直接返回根节点
return root;
// x的父节点 为红色 && x的祖父节点 不为空
if (xp == (xppl = xpp.left)) {
// 如果 x的父节点 为 x的祖父节点 的 左孩子
if ((xppr = xpp.right) != null && xppr.red) {
// 如果 x的祖父 的 右孩子 不为空 并且为红色
// x的祖父 的 左右孩子 都为黑色
// x的祖父 为 红色
xppr.red = false;
xp.red = false;
xpp.red = true;
// x 变为 x 的祖父-红色
x = xpp;
} else {
// 如果 x的祖父 的 右孩子 为空 或者为黑色
if (x == xp.right) {
// 如果 x 为父节点的 右孩子
// 左旋转
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
// 祖父节点为红色,父、叔节点为黑色
xp.red = false;
if (xpp != null) {
xpp.red = true;
// 右旋转
root = rotateRight(root, xpp);
}
}
}
} else {
// 如果 x的父节点 为 x的祖父节点 的 右孩子
if (xppl != null && xppl.red) {
// 如果 x的祖父 的 左孩子 不为空 并且为红色
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} else {
// 如果 x的祖父 的 左孩子 为空 或者为黑色
if (x == xp.left) {
// 如果 x 为父节点的 左孩子
// 右旋转
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
// 祖父节点为红色,父、叔节点为黑色
xp.red = false;
if (xpp != null) {
xpp.red = true;
// 左旋转
root = rotateLeft(root, xpp);
}
}
}
}
}
}
将代码进行拆解图示说明
x的父节点 为 x的祖父节点 的 左孩子:
-
如果 x的祖父 的 右孩子 不为空 并且为红色
if ((xppr = xpp.right) != null && xppr.red) { // x的祖父 的 左右孩子 都为黑色 // x的祖父 为 红色 xppr.red = false; xp.red = false; xpp.red = true; // x 变为 x 的祖父-红色 x = xpp; }变色:

-
如果 x的祖父 的 右孩子 为空 或者为黑色
-
如果 x 为父节点的 右孩子
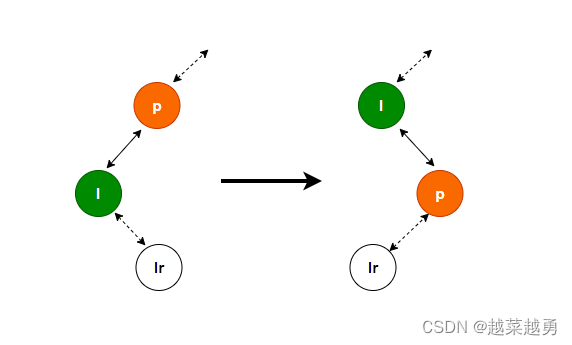
if (x == xp.right) { // 左旋转 root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; }左旋转(父节点 p):

-
如果 x 为父节点的 左孩子
if (xp != null) { // 祖父节点为红色,父、叔节点为黑色 xp.red = false; if (xpp != null) { xpp.red = true; // 右旋转 root = rotateRight(root, xpp); } }变色:
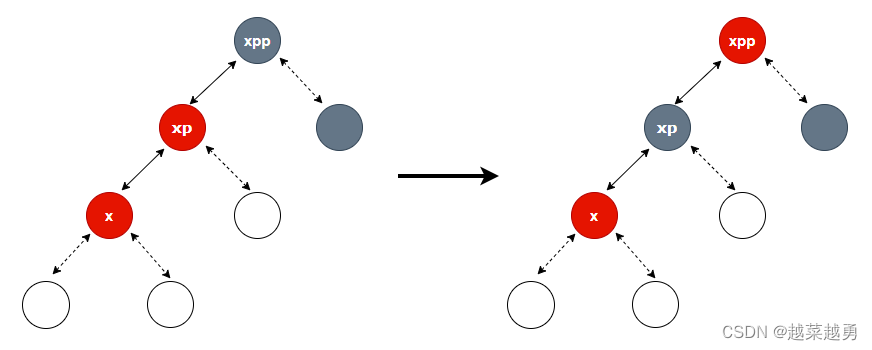
右旋转(祖父节点 p):
-
x的父节点 为 x的祖父节点 的 右孩子:
-
如果 x的祖父 的 左孩子 不为空 并且为红色
if (xppl != null && xppl.red) { xppl.red = false; xp.red = false; xpp.red = true; x = xpp; }变色:
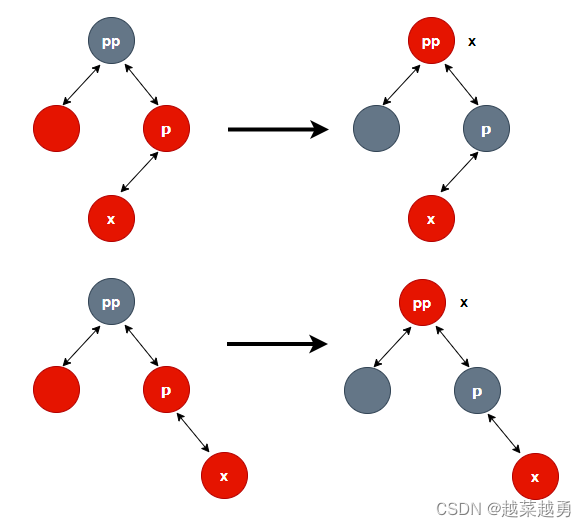
-
如果 x的祖父 的 左孩子 为空 或者为黑色
- 如果 x 为父节点的 左孩子
右旋转(父节点 p):if (x == xp.left) { // 右旋转 root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; }
- 如果 x 为父节点的 右孩子
变色:if (xp != null) { // 祖父节点为红色,父、叔节点为黑色 xp.red = false; if (xpp != null) { xpp.red = true; // 左旋转 root = rotateLeft(root, xpp); } }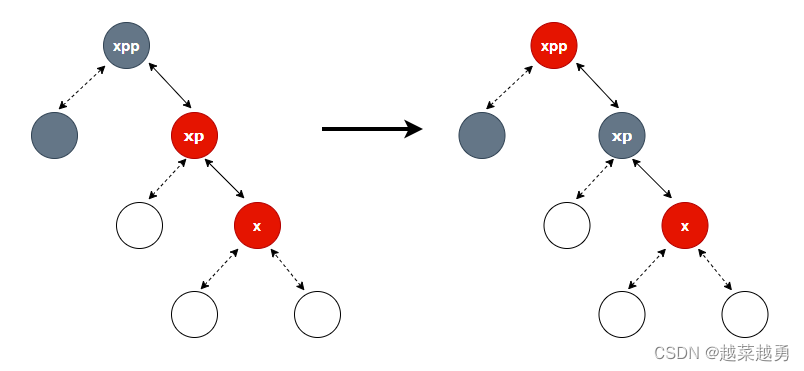
左旋转(祖父节点 p):
- 如果 x 为父节点的 左孩子











 本文详细介绍了红黑树相对于二叉搜索树和AVL树的优势,阐述了红黑树的五条核心规则,并提供了左旋、右旋以及插入平衡算法的代码实现。通过对插入节点时可能的失衡情况的处理,展示了如何通过旋转和颜色调整来维护红黑树的平衡,确保其在最坏情况下的查找效率仍为O(logN)。
本文详细介绍了红黑树相对于二叉搜索树和AVL树的优势,阐述了红黑树的五条核心规则,并提供了左旋、右旋以及插入平衡算法的代码实现。通过对插入节点时可能的失衡情况的处理,展示了如何通过旋转和颜色调整来维护红黑树的平衡,确保其在最坏情况下的查找效率仍为O(logN)。
















 2087
2087

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








