同态滤波器原理及其数字图像处理算法实现

第一次尝试写文章，希望可以巩固知识和分享知识。

1. #一、基础概念与模型

一幅图像f(x,y)能够用它的入射光分量和反射光分量来表示，其关系式如下

f(x,y)是由光源产生的照度场和目标的反射系数场的共同作用下产生的。该模型可作为频率域中同时压缩图像的亮度范围和增强图像的对比度的基础。

2. #二、算法分析与推导

但在频率域中不能直接对照度场和反射系数场频率分量分别进行独立的操作。可做出以下简单取对数运算：

其中，最后一步变换是傅里叶变换。已知，图像中的照明分量往往具有变化缓慢的特征，而反射分量则倾向于剧烈变化，特别在不同物体的交界处。由于这种持征，图像的自然对数的傅里叶变换的低频分量与照明分量相联系，而其高频分量则与反射分量相联系。利用上式，讲图像中的照明分量和反射分量分开，这样经过同态滤波可以分别作用在这两个分量上。如下处理：

滤波去噪后，经过快速傅里叶逆变换回到空域，最后对两边取指数实现同态滤波过程。
流程图如下：

可知，同态滤波的关键在于滤波函数的选择。同态滤波函数示意图：


同态滤波是一种特殊的高通滤波器，由于高通滤波能够衰减或者抑制低频分量，因此同态滤波器能对图像进行锐化处理。
由滤波函数示意图可知，同态滤波传递函数的波形和传统的巴特沃斯高通滤波器十分相似，而n阶巴特沃斯高通滤波器的传递函数为：

(2-1)
类比式子（2-1）的传递函数模型，根据同态滤波器的传递函数特性，可以对（2-1）做出改进。因为，退化的图像经过高通滤波之后，丢失了许多低频信息，平滑区基本消失，需要高频加强滤波来弥补，因此，可以在滤波传递函数中添加一个常数c ，取值范围为[0,1],从而得到一种与n阶巴特沃斯高通滤波器对应的同态滤波器自适应的传递函数：
（2-2）

**

3. #三、算法实现**
   ##同态滤波功能函数实现：

function im_e = omom_filter(im,d,rL,rH)
% 同态滤波
%函数输入: 
%         im:  输入的二维图像矩阵
%         d:   截止频率
%         rL   低频增益
%         rH   高频增益
%函数输出: 
%         im_e: 重构滤波图像
if ~isa(im,'double')
    im = double(im);
end
[r c]=size(im); % 输入图像维数
% 高斯高通滤波
A=zeros(r,c);
for i=1:r
    for j=1:c
        A(i,j)=(((i-r/2).^2+(j-c/2).^2)).^(.5);
        B(i,j)=A(i,j)*A(i,j);
        H(i,j)=(1-exp(-((B(i,j)).^2/d.^2)));% 传递函数
    end
end
% 同态滤波器传递函数：
H=((rH-rL).*H)+rL;
im_l=log2(im + 1e-5);% 取对数
im_f=fft2(im_l);% 离散傅里叶变换
im_nf=H.*im_f;% 滤波
im_n=abs(ifft2(im_nf));% DFT反变换
% 指数变换，消除取对数
im_e = exp(im_n);  % 滤波矩阵
im_e = uint8(im_e);

##主函数测试图片代码

%　同态滤波
clc,clear,close all  % 清理命令区、清理工作区、关闭显示图形
feature jit off      % 加速代码运行
tic
[filename ,pathname]=...
    uigetfile({'*.bmp';'*.tif';'*.jpg';},'选择图片'); %选择图片路径
str=[pathname filename]; % 合成路径+文件名
im = imread(str);        % 读图
im = imnoise(im,'gaussian',0,1e-3); % 原图像 + 白噪声
 
%同态滤波参数设置
rL = 0.3999;  % 低频增益
rH = 0.71;   % 高频增益
D0 = 1;   % 截止频率
figure,
subplot(121),imshow(im);title('原始图像')
colormap(jet)  % 颜色
shading interp % 消隐
im_e = Homom_filter(im,D0,rL,rH);   % 同态滤波
subplot(122),imshow(im_e,[]);title('同态滤波图像')
colormap(jet)  % 颜色
shading interp % 消隐
toc

#滤波结果：

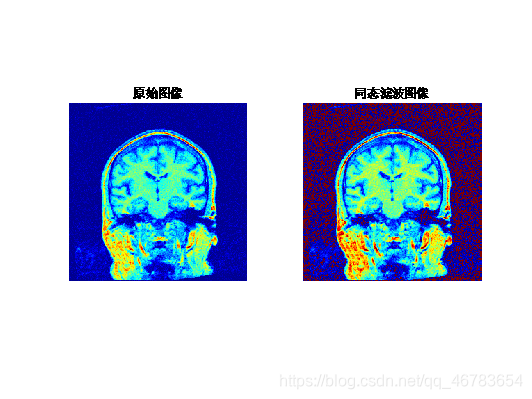
就写到这里啦，希望看到这个文章的同学能有所收获。
##一些注意点：
1、输入的图片需要深度为8位图像。
2、附录原图：