7-3 最小生成树-kruskal (10 分)(思路+详解+并查集详解+段错误超时解决)宝 Come

一：前言

本题需要用到并查集的知识，建议先学完并查集后再看看本题

二：题目

题目给出一个无向连通图，要求求出其最小生成树的权值。
温馨提示：本题请使用kruskal最小生成树算法。
输入格式:
第一行包含两个整数 N(1<=N<=1x10 6
),M(1<=M<=1x10 6
) 表示该图共有 N 个结点和 M 条无向边。接下来 M 行每行包含三个整数 X ，表示有一条长度为 Z 的无向边连接结点 X
输出格式:
输出一个整数表示最小生成树的各边的长度之和。

输入样例:

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出样例:

7

三：介绍kruskal

1:介绍kruskal

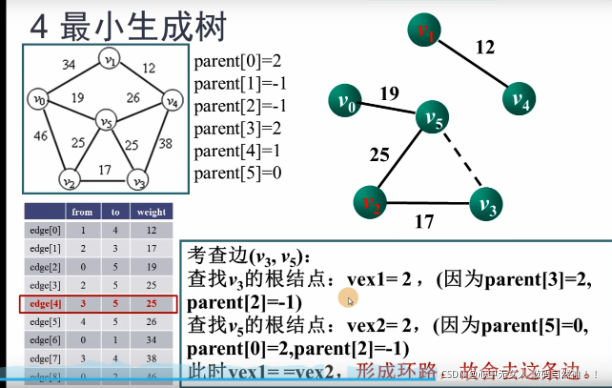
2：演示算法过程就是并查集的过程

形成环：即顶点3和5的根节点为同一个结点那么就不用合并

四:思路

思路：
1.用kruskal算法是从边的角度出发的每次选取最小的边
2.这里涉及到并查集，回归到本题就是先将每个顶点当成一个联通分量（也是一棵树）
并设置其父节点都为 -1，表示根节点，如果两个连通分量根节点不同，那么将其合并，
同时更新其中一个连通分量的根节点为另一个连通分量的根节点
那么到最后就会形成一个根节点，此时图的各个结点也是连通的，我们在每次计算是否合并
两个连通分量的时候，我们就已将权值进行相加，那么这样的结果是最小生成树

3.那么我们就需要对边进行升序排序了，按顺序每次选取最小的边

4.这里考虑到还要对权值进行升序处理，而且是按一组数据中的某个元素 升序处理
那么这里我们就不再用邻接矩阵和邻接表来存数据了，用结构体数组来存每组数据
同时通过重写sort方法来处理升序问题

5.那么通过上方的分析你还有另外一个收获，判断图是否连通，哈哈哈，如果最后的father数组
中每个结点的根节点都是同一个值 那么说明他是连通的 （这里的结点指的是father数组当中的下标）

五：上码

/**
 	思路：
	 1.用kruskal算法是从边的角度出发的每次选取最小的边
	 2.这里涉及到并查集，回归到本题就是先将每个顶点当成一个联通分量（也是一棵树） 
	   	并设置其父节点都为 -1，表示根节点，如果两个连通分量根节点不同，那么将其合并，
	 	同时更新其中一个连通分量的根节点为另一个连通分量的根节点
		 那么到最后就会形成一个根节点，此时图的各个结点也是连通的，我们在每次计算是否合并
		 两个连通分量的时候，我们就已将权值进行相加，那么这样的结果是最小生成树 
		 
		 	 
	 3.那么我们就需要对边进行升序排序了，按顺序每次选取最小的边
	 
	 4.这里考虑到还要对权值进行升序处理，而且是按一组数据中的某个元素  升序处理
	 	那么这里我们就不再用邻接矩阵和邻接表来存数据了，用结构体数组来存每组数据
		 同时通过重写sort方法来处理升序问题 
		 
	5.那么通过上方的分析你还有另外一个收获，判断图是否连通，哈哈哈，如果最后的father数组
	只输出一个值 那么说明他是连通的		 
	
*/ 

#include<bits/stdc++.h>
using namespace std;
#define maxx 1000010//这里需要7位数

//定一结构体数组来存每组数据 
struct Node{
	int from;
	int to;
	int val; 
	
}node[maxx]; 

int father[maxx];

bool sort_val(Node a,Node b){
	return a.val < b.val;
}

//查询元素的根节点 
int find( int a ){
	int r=a;
    while(father[r]!=r)
    r=father[r];		//找到他的前导结点
    int i=a,j;
    while(i!=r){	//路径压缩算法
       j=father[i];	//记录x的前导结点
       father[i]=r;	//将i的前导结点设置为r根节点
       i=j;
    }
    return r;
}


//合并根节点不同的联通分量 
void merg(int a,int b){
	
//	int a = find(x);//查询x的根节点 
//	int b = find(y);//查询y的根节点 
	
//	if(a != b){
		father[a] = b;	
//	} 	
}

int main(){
	
	int n,m;
	int sum = 0;
	
	//cin >> n >> m;
	scanf("%d%d",&n,&m);
    
	//初始化father数组 将其每个顶点的根节点设置为自己的节点号
	for(int i = 1; i <= n; i++){
		father[i] = i;
	} 
	
	for(int i = 0; i < m; i++){		
		//cin >> node[i].from >> node[i].to >> node[i].val;
      scanf("%d%d%d",&node[i].from,&node[i].to,&node[i].val);
	}
		
	sort(node,node+m,sort_val);
	
//	for(int i = 0; i < m; i++){
//		cout << node[i].val << endl;
//	}

    int count = 0;
    
	for(int i = 0; i < m; i++){		
        if(count == n - 1){//n个顶点需要 n - 1边
            break;
        }
		int a = find(node[i].from);
		int b = find(node[i].to);
		if(a != b){
			father[a] = b;
			sum += node[i].val;			
		    count++;
        }	
       
	}
	printf("%d",sum);
    // cout << sum; 	
}
 

六：知识速递（对并查集不了解的兄弟们可以了解下）

这道题用到了并查集，所以我就学了一下并查集，所以把自己的见解也分享给大家（建议 先看视频 再浏览 博客 再自己敲一遍 学习效率高而已，我总是乱着来 以为看几篇博客就会了，其实最后还是老老实实 去B站看大佬讲解视频 才搞懂）

1:并查集

并查集是一种树型的数据结构，
用于处理一些不相交集合（Disjoint Sets）的合并及查询问题
1：查询元素a和元素b是否属于同一组
2：合并元素a和元素b所在组 （将有相同元素的元素 合并为一个组 ）
3：需要初始化一个数组存放父节点，其索引值 代表元素

2：并查集的AC代码（模板`）

/*
并查集是一种树型的数据结构，
用于处理一些不相交集合（Disjoint Sets）的合并及查询问题

1：查询元素a和元素b是否属于同一组
2：合并元素a和元素b所在组 （将有相同元素的元素 合并为一个组 ）
3：需要初始化一个数组存放父节点，其索引值 代表元素
*/

#include<bits/stdc++.h>
using namespace std;
 
int father[100]; 
 

int find( int x){
	
	while( x != father[x] )
	{
		x = father[x];
	}
		
	return x;		
} 

void merge(int x,int y)
{
	int a = find(x);//x的根节点为a 
	int b = find(y);//y的根节点为b
	if( a != b )
	father[b] = a;//那么将b的根节点  设为 a 
	 
}


int main()
{
	//初始化： 我们将每一个结点的前导结点设置为自己，
	//如果在merge函数时未能形成连通，将独立成点
	for( int i = 0; i < 10; i++ )
	{
		father[i] = i;
	}
	

上方的find函数 效率不高，当处理大数据时，使用并查集查找时，如果查找次数很多，那么使用朴素版的查找方式肯定要超时。比如，有一百万个元素，每次都从第一百万个开始找，这样一次运算就是106，如果程序要求查找个一千万次，这样下来就是1013,肯定要出问题的。

所以有了压缩路径的算法（就是一棵树只有叶节点）

int find( int a ){
	int r=a;
    while(Father[r]!=r)
    r=Father[r];		//找到他的前导结点
    int i=a,j;
    while(i!=r){	//路径压缩算法
       j=Father[i];	//记录x的前导结点
       Father[i]=r;	//将i的前导结点设置为r根节点
       i=j;
    }
    return r;
}

七：超时和段错误解决

1.超时建议将cin cout改为scanf 和printf
2.段错误建议将上方的开辟最大值调至 七位数