【紫书第十章】数论与概率入门

一、数论初步

1.欧几里得算法(辗转相除法)

在求两个数的最大公因数时，我们通常使用欧几里得算法来求解。

int gcd(int a,int b)
{
	if(b==0)return a;
	else return gcd(b,a%b);
}

最小公倍数：(a*b)/最大公约数

int lcm(int a,int b)
{
	return a/gcd(a,b)*b;   //这么写可以防止溢出
}

2.素数筛-埃氏筛

埃氏筛是用每个数的所有质因子去筛掉他这个数。
每个数的根号以内所有质因子会筛掉这个数。
从这个可以看出给定 个数，每个数被筛的次数就是质因子的个数。复杂度O(nloglogn)。
代码：
合数10 = 2*5

int Eratosthenes(int n) {
	int p = 0;
	for (int i = 0; i <= n; ++i) is_prime[i] = 1;
		is_prime[0] = is_prime[1] = 0;
	for (int i = 2; i <= n; ++i) {
		if (is_prime[i]) {
			prime[p++] = i; // prime[p]是i,后置自增运算代表当前素数数量
			for (int j = i * i; j <= n; j += i)
				is_prime[j] = 0; // i的倍数的均不是素数
				// 因为从 2 到 i - 1 的倍数我们之前筛过了，这里直接从 i
				// 的倍数开始，提高了运行速度
		}
	}
	return p;
}

3.素数筛-欧拉筛

利用了合数的性质，一个非素数必定是素数的乘积，特点是每个数只被筛过一遍。每个数被自己最小的质因子筛去，复杂度是O(n)

void init() {
	for (int i = 2; i < MAXN; i++)is_prime[i] = 1;
	for (int i = 2; i < MAXN; ++i) {
		if (is_prime[i]) {
			pri[cnt++] = i;
		}
		for (int j = 0; j < cnt && pri[j] * i < MAXN; ++j) {
			is_prime[i * pri[j]] = 0;
			if (i % pri[j] == 0) { break; }
			// i % pri[j] == 0
			// 换言之，i 之前被 pri[j] 筛过了
			// 由于 pri 里面质数是从小到大的，所以 i 乘上其他的质数的结果一定也是
			// pri[j] 的倍数 它们都被筛过了，就不需要再筛了，所以这里直接 break
			// 掉就好了
		}
	}
}

4.扩展欧几里得算法

• 概念：求解ax+by=gcd(a,b)方程的解

void gcd(int a, int b, int& d, int& x, int& y)
{
	if (!b)
		d = a, x = 1, y = 0;
	else
		gcd(b, a % b, d, y, x), y -= x * (a / b);
}

通过上述函数，我们求得一组解（x₀,y₀）;

• 其它所有解为（x₀+kb’,y₀-ka’）
• a’=a/gcd(a,b);
• b’=b/gcd(a,b);
• k是任意整数；

推广到任意ax+by=c:当c不为gcd(a,b)整数倍时无整数解。

5.快速幂

用途：求解 aⁿ %mod问题
博客链接：快速幂问题

int qmi(int m, int k, int p)//求m的k次方取余于p
{
	int res = 1%p, t = m%p;
	while (k)
	{
		if (k & 1)//{等效于if(k%2==1)}判断k转化为2进制后最后一位数是不是1
		{
			res = res * t % p;
		}
		t = t * t % p;
		k >>=1;//2进制数/2,即2进制删除最后一位数{等效于k/=2}
	}
	return res;
}

二、概率基础

1.容斥原理

求1~n中能被x，y，z整除的个数

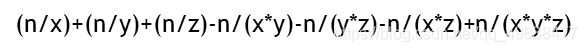
• 解释：一般来说，对于任意多个集合都可以列出这样一个等式，左边是所有集合的并的元素个数。右边是这些元素的各种组合。每一个组合都是若干个集合的交集，并且每一项前面的正负号取决于集合的个数：奇数个集合为正，偶数个集合为负。

2.杨辉三角和二项式定理

• 概念：见高中教科书
• 求C[n][k]的方法
  • C[n][k]=C[n-1][k]+C[n-1][k-1] (复杂度O(n²)，太慢了不实用)
  • C[n][k]=((n-k-1)/k)*C[n][k-1]，通过C[n][0]=1递归求解。一般写成C[n][k]=(n-k-1)*C[n][k-1]/k，先乘后除是为了考虑先除后不为整数的问题。
• 关于组合数的一些性质
  

3.离散概率基础

• P(A|B):事件B发生的前提下A发生的概率
• P(AB):事件A和B都发生的概率：P(AB)=P(A)*P(B)
• 条件概率：P(A|B)=P(AB)/P(B)；P(A|B)=P(B|A)*P(A)/P(B)
• 全概率公式：P(A)=P(A|B₁)*P(B₁)+P(A|B₂)*P(B₂)+…+P(A|B_N-1)*P(B_N-1)+P(A|B_N)*P(B_N);

三、其它数学专题

1.汉诺塔

• 概念：汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？
  
  
• 公式：f(1)=1，f(k+1)=2f(k)+1

2.斐波拉契数列

• 概念：不会有人不知道吧…fn=fn-1+fn-2(n>=2) f0=0,f1=1;
• 性质
  • 模除周期性：数列的数模除某个数的结果会呈现一定周期性，因为数列中的某个数取决与前两个数，一旦有连着的两个数的模除结果分别等于第0 第一项的模除结果，那麽代表着一个新的周期的的开始，如果模除n，则每个周期中的元素不会超过n×n;
  • 黄金分割：随着i的增大Fi/Fi-1 接近于0.618.
  • 平方与前后项：从第二项开始，每个奇数项的平方都比前后两项之积多一，每个偶数项的平方比前后两项之积少一.
  • 斐波那契数列的第n+2项代表了集合{1，2，…n}中所有不包含相邻正整数的子集的个数.
  • 隔项关系：f(2n-2m-2)[f(2n)+f(2n+2)]=f(2m+2)+f(4n-2m) [ n〉m≥-1，且n≥1
  • 两倍项关系：f(2n)/f(n)=f(n-1)+f(n+1)
  • 尾数循环：个位数：周期60；最后两位：300；最后三位：1500

作者：Avalon Demerzel，喜欢我的博客就点个赞吧，更多紫书知识点请见作者专栏《紫书学习笔记》