【灵巧手抓握】ILDA算法学习：同类别不同物体的抓握泛化——Learning Generalizable Dexterous Manipulation from Human Grasp

综述

论文题目：《Learning Generalizable Dexterous Manipulation from Human Grasp Affordance》

论文出处：CoRL2022

论文链接：https://proceedings.mlr.press/v205/wu23a/wu23a.pdf

源码链接：https://kristery.github.io/ILAD

背景

​  为了使机器人在日常生活中能够灵活地协助人类，多指机器手的灵巧操作是机器人操作任务中的核心问题。但是，由于灵巧手具有高自由度的关节（自由度一般从24DoF到30DoF），控制算法想要实现自然、且合乎物理的抓取操作非日常难，算法的泛化性能难以达到较好的保障。虽然强化学习（RL）的最新工作在复杂灵巧操作方面取得了一定的进展，但是他仍受到训练中大量样本要求的限制，并且训练后的策略难以推广部署到新的物体上。

​  为了提高训练中的样本效率，一个主流方向是从人类演示中进行模仿学习，人类可以利用Mocap和视频从虚拟现实（VR）中的遥控操作中收集灵巧操作的专家演示。以人类为指导，他不仅降低了学习中的样本复杂度，而且还可以帮助机械手做出像人类一样的安全行为。然而，当前的数据收集设置在很大程度上限制了演示的规模和多样性，由于每个数据都需要部署人力来采集，获取大规模的训练数据成本较高，算法的泛化性能难以得到有效的提升。并且由于数据有限，学习到的策略很难泛化到训练过程中未见过的物体上。

主要思想

​​  在本文中，作者提出了一种新的灵巧抓握方法，可以实现同一类别中的新物体实例的抓握泛化，也就是实现同类别多对象的抓握。作者首先根据现有的人类抓握可供性模型（human grasp affordance model）生成人类手与同一类别中不同物体交互的大规模演示（demonstration）（如下图左侧所示）。具体地来说，我们可以利用人类抓握可供性模型生成人手的抓握姿势和接触方式（可参考算法GraspTTA），之后利用运动规划算法生成一条轨迹，将机械手从起始状态移动到目标抓握状态，该轨迹部分演示了机械手如何像人类一样到达并稳定地抓取物体，为后续的任务做准备。然后，使用模仿学习来训练策略，通过使用这些演示增强RL，并在未见过的物体上进行测试（如下图右侧所示）。策略算法将物体点云和机械手状态作为决策的输入，通过联合学习来解决泛化问题：

• 使用新的模仿学习目标进行技能泛化；
• 使用行为克隆目标进行几何表示的泛化；

模仿学习目标：为了学习策略，作者使用生成的演示来增强强化学习策略，以进行模仿学习。以前的方法在学习过程中对所有演示赋予同等权重。为了利用多样化和大规模的演示，作者提出了一种新颖的排名函数，用于鼓励策略从不太可能重现的轨迹中学习。此外，作者根据 权重不断增加的演示 来估计状态-动作对的优势值，以便该策略在后期训练阶段仍可以从给定的演示中受益。

几何表征学习：策略需要根据点云输入来理解对象形状，以便对其进行相应的操作。作者利用PointNet对输入对象的点云进行编码，并使用大规模演示，通过行为克隆任务对表示进行预训练。随着策略在学习过程中与环境不断做交互，算法会收集新数据以继续通过行为克隆对PointNet进行微调，该流程联合优化了技能泛化的模仿学习目标和表征泛化的行为克隆目标。

​  作者的贡献点主要为：

• 一种针对不同物体生成大规模灵巧操作演示的新方法；
• 一种用于泛化灵巧操作的新颖模仿学习目标和3D几何表示学习方法；
• 比基线方法显著改进了对新物体的灵巧操作。

方法

为了更方便地表述，本节均用第一人称描述。

​  我们的策略的全称为（Imitation Learning f rom Affordance Demonstration, ILAD）将物体点云和手关节状态作为输入，整个策略结构分为两个阶段：

• 可供性演示生成（Affordance Demonstration Generation）：利用最先进的抓握姿态预测模型GraspCVAE来生成同一类别中不同物体的不同抓握动作，并且利用运动规划来获取实现这些抓握动作的轨迹。虽然这些轨迹并未展示如何执行特定的任务，但他们可以作为指导我们的策略实现抓握动作中正确接触的部分演示。
• 带有表征学习的模仿学习（Imitation Learning with Representation Learning）：我们提出了一种新的模仿学习目标，通过可供性演示来学习策略。同时，我们还提出了一种与模仿学习相结合的3D几何表示学习方法。

可供性演示生成

​ 算法的主要流程图如下所示：

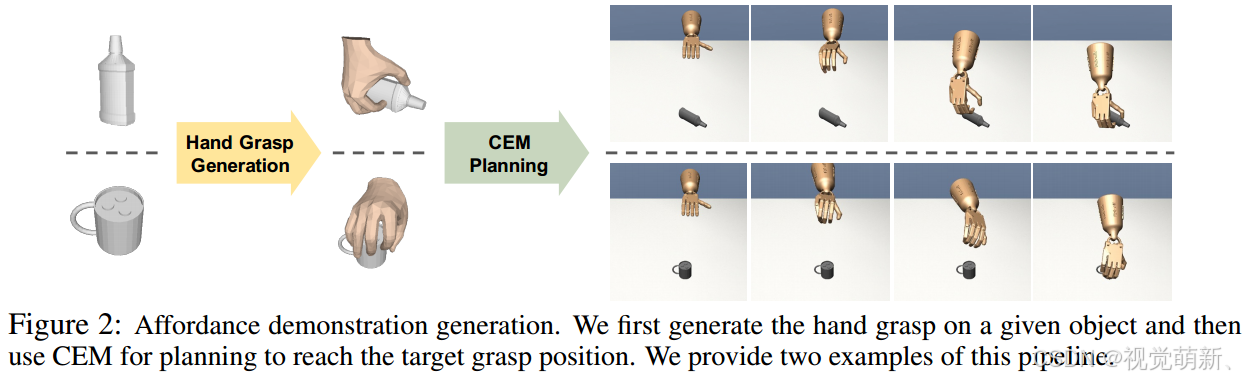
抓握生成

​  给定不同的3D物体，我们采用预先训练的GraspCVAE模型为每个物体生成不同的人类抓握动作。具体地来说，GraspCVAE以点云观测为输入，并输出由形状参数$\beta$和姿势参数$\alpha$参数化的MANO模型表示的抓握姿态。利用这些参数，我们可以使用正向运动学函数$j^h={\mathcal{J}}_h(\beta ,\alpha )$计算人手关节。

抓握轨迹的运动规划

​  给定目标抓握手部姿势的关节$j^h$，我们的目标是找到一个机器人手部动作序列$a_1,\dots ,a_K$，该序列生成机器人手部关节序列$j_0^r,\dots ,j_K^r$，使得最后的机器人手关节位置$j_K^r$达到$j^h$，这一过程就是抓握轨迹的运动规划过程，手部姿态逐步朝着目标抓握姿态做改变。注意，给出了初始机器人手关节$j_0^r$，运动规划的优化目标为：
$$\underset{a_1,\dots ,a_K}{\min }||j_K^r-j^h|{|}^2+\lambda ||p_K-p_1|{|}^2$$
其中$p_1$和$p_K$是时间步$1$和$K$处的物体姿势，常数$\lambda$为10，目标的第一项用于鼓励机械手臂逐步转变为预测的抓握姿态，第二项防止物体在此过程中移动，中间可能受到手的抓握影响，可以产生偏移，主要是约束初始位置和截止位置要尽可能相同。考虑到这个目标，我们使用交叉熵方法来进行运动规划，首先从高斯分布$G(\mu ,diag({\sigma }^2))$中抽取动作，并挑选固定数量的低成本候选对象，我们使用这些候选对象更新$\mu$和$diag({\sigma }^2)$，并且迭代重复，同时使用模型预测控制（model predictive control, MPC）执行计划的轨迹，直到目标低于阈值$\delta$，此时生成的动作序列可以当做抓握该物体的标签，用于后续的模仿学习，训练模型的参数，有点类似数据生成。

模仿学习

​​  我们使用规划算法生成的演示进行模仿学习。

准备工作

​  我们首先考虑一个标准的马尔科夫决策过程（MDP），它由一个元组$<S,A,P,R,\gamma >$表示，其中$S$和$A$为状态和动作空间，$P(s_{t+1}|s_t,a_t)$是在状态$s_t$时执行动作$a_t$的情况下，在步骤$t+1$时的状态$s_{t+1}$转移密度。$R(s,a)$是奖励，$\gamma$为折扣因子，强化学习的目标是使策略$\pi (a|s)$最大化预期奖励，我们使用一种基于DAPG（Demo Augmented Policy Gradient）的模仿学习基线算法构建了我们的方法，第$k$个时期的学习目标函数可以表示为：
$$g_{aug}=\sum _{(s,a)\in D_{{\pi }_{\theta }}}{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s)A^{{\pi }_{\theta }}(s,a)+\sum _{(s,a)\in D_{{\pi }_{\mathrm{E}}}}{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s){\lambda }_0{\lambda }_1^k\underset{(s,a)\in D_{{\pi }_{\theta }}}{\max }{A}^{{\pi }_{\theta }}(s,a),$$
其中$A^{{\pi }_{\theta }}$为优势函数，用于根据策略${\pi }_{\theta }$估计从$(s,a)$和$s$开始的折扣奖励总和的差值，$D_{{\pi }_E}$是来自专家演示的状态-动作对，$D_{{\pi }_{\theta }}$是使用策略${\pi }^{\theta }$收集的状态-动作对，${\lambda }_0$和${\lambda }_1$为超参数，为了保证训练过程中的稳定性，${\max }_{(s,a)\in D_{{\pi }_{\theta }}}{A}^{{\pi }_{\theta }}(s,a)$为1。

从多个物体的部分演示中学习

​  为了将灵巧操作推广到多个物体中（例如更容易或更具有挑战性的形状），演示（demonstration）在训练过程中不应该平等对待，我们根据对象的抓取难度和策略的学习进度自适应地对演示进行排序，排序目标为：
$$\begin{array}{rl}{g}_{ILAD}=& \sum _{(s,a)\in D_{{\pi }_{\theta }}}{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s)A^{{\pi }_{\theta }}(s,a)+\sum _{(s,a)\in D_{{\pi }_{\mathrm{E}}}}{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s){\lambda }_0{\lambda }_1^k{w}_k(s,a)+\\ & \sum _{(s,a)\in D_{{\pi }_{\mathrm{E}}}}{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s){\lambda }_0^{\prime }(1-{\lambda }_1^k)A_{\varphi }^{{\pi }_{\theta }}(s,a),\end{array}$$
其中，第二项中的$w_k(s,a)$为标准的对数似然的负数，用于鼓励策略从 当前策略难以重现的轨迹 中学习，可以表示为：
$$w_k(s,a)=\frac{l_k({\tau }_{s,a})-{\min }_{\tau }{l}_k(\tau )}{{\max }_{\tau }{l}_k(\tau )-{\min }_{\tau }{l}_k(\tau )}$$
其中，${\tau }_{s,a}$是来自包含状态-动作对$(s,a)$的演示轨迹，轨迹的对数似然的负数为：
$$\begin{array}{r}{l}_k(\tau )=-\frac{1}{|\tau |}\sum _{(s,a)\in \tau }\log \mathrm{Pr}(s,a|{\pi }_{\theta })\end{array}$$
​  第三项中的$A_{\varphi }^{{\pi }_{\theta }}$是用$\varphi$参数化的模型针对 演示的状态-动作对 估计的优势函数。

​  在实验中，作者发现使用普通的方法训练抓取策略，可以轻松地学会操纵某种类型的物体，而忽略其他物体。为了鼓励该策略对各种物体进行泛化，我们使用归一化似然权重$w_k$，动态地为当前时期可能性小的演示分配更大的权重。

​  第三项的演示优势近似旨在进一步提高演示的利用率，虽然在之前的方法中，演示的优势取值为1，但是为了更准确地估计梯度，我们近似真实的优势。我们训练神经网络$A_{\varphi }^{{\pi }_{\theta }}$来预测优势函数，新的优势函数用强化学习训练过程中收集的数据进行训练，并应用于部分演示，${\lambda }_0^{\prime }=0.1{\lambda }_0$，防止过度的参数调整。

使用几何表征进行策略训练

​​  我们的策略将物体的点云、物体的6D姿势、机器人关于手关节状态作为输入，并预测动作。具体地来说，为了表示物体的形状，我们利用PointNet编码器${\theta }_{pc}$作为点云输入，给定点云编码，我们将其与物体的6D姿势参数和手关节状态连接在一起（机器人本体状态），并将他们一起传入3层MLP网络进行决策判断，因此，策略网络由 θ = { θ p c , θ p } \theta=\{\theta_{pc},\theta_p\} θ={θpc​,θp​}参数化。在训练过程中，我们还设计了一个几何表示学习目标来联合训练PointNet的参数，模型整体架构图如下图所示：

用于几何表示学习的行为克隆

​​  我们利用行为克隆来训练PointNet编码器，直接从策略学习中与环境交互期间收集的示例$D_{{\pi }_{\theta }}$中获取训练数据，具体而言，行为克隆目标可以表示为：
$${\mathcal{L}}_{bc}=\frac{1}{|D_{{\pi }_{\theta }}|}\sum _{(s,a)\in D_{{\pi }_{\theta }}}\Vert {\pi }_{\theta }(s)-a{\Vert }^2(2)$$
我们仍然利用包括决策MLP ${\theta }_p$在内的整个网络 θ = { θ p c , θ p } \theta=\{\theta_{pc},\theta_p\} θ={θpc​,θp​}来计算损失，仅通过反向传播来优化PointNet的参数$p_{pc}$，这部分对应于图3的上半部分。

预训练

​​  相同的优化目标也可用于在用演示$D_{{\pi }_E}$进行策略学习之前对 PointNet 编码器和策略网络进行预训练。

联合两个目标进行学习

​  我们联合模仿学习目标和行为克隆目标来训练我们的策略，我们发现在强化学习中使用策略梯度训练PointNet（第一个公式）会使决策的表示不稳定。在强化学习中，梯度的方差要大得多，直接学习具有高维输入的编码器非常具有挑战性。因此，我们建议为两个目标共享网络参数 θ = { θ p c , θ p } \theta=\{\theta_{pc},\theta_p\} θ={θpc​,θp​}，但使用策略梯度来优化决策MLP ${\theta }_p$和行为克隆来优化PointNet编码器${\theta }_{pc}$，也就是说第一个公式的梯度变成了关于${\theta }_p$的，而不是$\theta$的。

​  为了获得更好的稳定性，我们对PointNet编码器执行较慢的更新，以便决策从类似的表示中学习。具体地来说，我们使用策略梯度更新每个时期的MLP ${\theta }_p$，同时我们每个$T$时期再使行为克隆对PointNet编码器${\theta }_{pc}$执行一次更新，在图3中，不同颜色的箭头代表不同的更新策略，学习过程可以总结为：

先利用公式（2）来对${\theta }_{pc}$和${\theta }_p$做预训练，之后同时利用公式（2）和公式（1）做微调。

实验

​​  作者对五个物体类别的任务进行了实验：瓶子、遥控器、杯子、罐子和相机。在这个任务中，一个物体以随机的方向和位置放在桌子上，机器人需要抓住物体并将其移动到随机的目标位置。对于每个类别，作者使用40个物体进行训练，并且使用大约 30 个未见过的物体（因类别而异）进行测试，用于评估通用性，对于每组实验物体不同但是类别相同。

​​  作者采用TRPO作为我们的 RL 基线，并且还与DAPG进行了比较。为了公平比较，作者使用与 ILAD 相同的PointNet预训练方法，并使用它来处理DAPG的点云输入，即DAPG+PC。实验细节具体可以参考原文描述。

以上仅是笔者的个人见解，若有问题，欢迎指正。