毫米波雷达——毫米波阵列的MUSIC算法

1、MUSIC算法简介

MUSIC(Multiple Signal Classification)算法，即多信号分类算法，是一种基于子空间分解/矩阵特征空间分解的算法。MUSIC算法对DOA(波达方向)的估计有很高的分辨率。但是该算法的前提是入射信号（认为是不同角度目标的反射信号）必须是互不相干的。Plus：相干怎么处理？？？待补充
信号处理的观测空间可以分解为信号子空间和噪声子空间，信号子空间和噪声子空间具有正交性。信号子空间由阵列接收到的数据的协方差矩阵中与信号对应的特征值较大的特征向量组成，噪声子空间则由协方差矩阵中所有最小特征值（噪声方差）对应的特征向量组成。而噪声特征向量与空间导向矢量阵正交（后续会证明），以此通过寻找使之乘积最小的角度来估计波源方向。
计算步骤：计算协方差矩阵，构建空间谱函数、通过谱峰搜索，估计信号的参数。

2、阵列信号模型

MIMO等效为1发多收：假设有一个发射天线TX发射一个chirp。有N个接收天线RX组成均匀线性阵列，接收阵列天线之间的间距为半波长$d=\frac{\lambda }{2}$。(在MIMO里面，例如3发4收可以等效为1发12收，【发送的chirp信号可以通过各种**多址技术(eg. TDMA, CDMA, FDMA)**使之不发生混叠】，不同的发射天线TX之间距离间隔，恰好使得接收信号相位相差能够保持等差排列；【例如对于3发4收，接收天线之间的横向间隔为$d=\frac{\lambda }{2}$，而发射天线之间的间隔为有N个接收天线RX，发射天线TX之间的间距可以为$4\cdot \frac{\lambda }{2}$，从而第一个发射天线与最后一个接收天线之间的差为$3\cdot \frac{\lambda }{2}$，而第二个发射天线与第一个接收天线之间的差为$4\cdot \frac{\lambda }{2}$，形成等差数列】MIMO可以等效为单发多收的雷达。
信号源反射信号互不相关假设：假设有M个入射信号源，(可以认为是M个目标在同一个chirp下产生的回波信号)，分别从不同的方向入射到接收阵列，每个接收天线RX的入射信号和噪声互不相关，入射信号源的功率相同且互不相干。
图示M信号源与N接收天线模型：如下图所示，以最左侧的接收天线为参考点，各个接收天线的位置相比前一个增加距离d（一般为半波长）。其中一个信号$S_1(t)$的入射方向角为$\theta$，表示入射信号与线阵法线的夹角，[一般假设信号源数目(目标数目)M小于阵元数目N]。Plus：为什么要小于？如果目标数不知道该如何处理？待补充

建立接收信号模型：在第t时刻的快时间采样 （每个chirp里面256或512个数据为快时间采样；不同chirp中，相同位置的采样点数为慢时间采样），假设得到的接收数据模型为：
$$\mathbf{X}(t)=\mathbf{A}(\theta )\cdot \mathbf{S}(t)+\mathbf{N}(t)$$
其中
$$\mathbf{X}(t)=\left(\begin{array}{c}{\mathbf{X}}_1(t)\\ {\mathbf{X}}_2(t)\\ ⋮\\ {\mathbf{X}}_N(t)\end{array}\right)$$
$\mathbf{X}(t)$是一个N行的矩阵，N行是因为指阵列有N个阵元。上面公式里面噪声部分形式最简单，先看噪声部分：
$$\mathbf{N}(t)=\left(\begin{array}{c}{\mathbf{N}}_1(t)\\ {\mathbf{N}}_2(t)\\ ⋮\\ {\mathbf{N}}_N(t)\end{array}\right)$$
$\mathbf{N}(t)$是噪声矩阵，为了简便，一般认为是高斯白噪声，不同接收天线的噪声分量相互独立，互补相关。
回波信号部分：
$$\mathbf{S}(t)=\left(\begin{array}{c}{\mathbf{S}}_1(t)\\ {\mathbf{S}}_2(t)\\ ⋮\\ {\mathbf{S}}_M(t)\end{array}\right)$$
值得注意的是：$\mathbf{S}(t)$是一个M行的矩阵，表示M个信号源发出的信号，即空间中一共有M个信号源，（表示M个目标反射到雷达的入射信号），【每个信号源到接收天线的角度都是不同的，但在符合远场条件下，一般认为同一个信号源到不同接收天线的角度是相同的】。
下面重点分析角度矩阵(导向矢量矩阵)：$\mathbf{A}(\theta )$，直接给出：
$$\mathbf{A}(\theta )=\left[\begin{array}{cccc}1& 1& \dots & 1\\ e^{-j2\pi \frac{d\sin {\theta }_1}{\lambda }}& e^{-j2\pi \frac{d\sin {\theta }_2}{\lambda }}& \dots & e^{-j2\pi \frac{d\sin {\theta }_M}{\lambda }}\\ ⋮& ⋮& \ddots & ⋮\\ e^{-j2(N-1)\pi \frac{d\sin {\theta }_1}{\lambda }}& e^{-j2(N-1)\pi \frac{d\sin {\theta }_2}{\lambda }}& \dots & e^{-j2(N-1)\pi \frac{d\sin {\theta }_M}{\lambda }}\end{array}\right]$$
写成向量的形式为：
$$\mathbf{A}(\theta )=\left[\begin{array}{cccc}\alpha ({\theta }_1)& \alpha ({\theta }_2)& \dots & \alpha ({\theta }_M)\end{array}\right]$$
值得注意的是，写成向量的形式后，这里有M个列向量，这与$\mathbf{S}(t)$对应。$\mathbf{A}(\theta )$是一个$N\times M$的空间阵列的导向矢量阵(方向角度矩阵)。
因此，$\mathbf{A}(\theta )\cdot \mathbf{S}(t)$为：
$$\mathbf{A}(\theta )\cdot \mathbf{S}(t)=\left[\begin{array}{c}\alpha ({\theta }_1){\mathbf{S}}_1(t)+\dots +\alpha ({\theta }_M){\mathbf{S}}_M(t)\end{array}\right]$$
带入得：
$$\mathbf{A}(\theta )\cdot \mathbf{S}(t)=\left[\begin{array}{c}{\mathbf{S}}_1(t)+{\mathbf{S}}_2(t)+\dots +{\mathbf{S}}_M(t)\\ e^{-j2\pi \frac{d\sin {\theta }_1}{\lambda }}{\mathbf{S}}_1(t)+\dots +e^{-j2\pi \frac{d\sin {\theta }_M}{\lambda }}{\mathbf{S}}_M(t)\\ ⋮\\ e^{-j2(N-1)\pi \frac{d\sin {\theta }_1}{\lambda }}{\mathbf{S}}_1(t)+\dots +e^{-j2(N-1)\pi \frac{d\sin {\theta }_M}{\lambda }}{\mathbf{S}}_M(t)\end{array}\right]$$
从上式可得，上式的每行代表所有信号分量到这一个接收天线的分量的叠加。对第i个接收天线（即第i行），他的输入信号分量包含每个信号源的信号经过一段相位延时（这是由于接收天线阵列排布导致的）的信号，(这个相位延迟与该信号源的角度有关，同时还与他传到第几个接收天线有关【认为最左边的天线是1号接收天线，表示0相位延迟】)，【这里的延迟是由于信号源到不同接收天线所带来的微小相位延迟，而不是不同距离带来的大延迟】【角度估计，一般认为目标在同一距离单元内】，所有的信号源经过一些相位延迟的信号总和，就是进入该接收天线的信号分量。
因此 $\mathbf{X}(t)=\mathbf{A}(\theta )\mathbf{S}(t)+\mathbf{N}(t)$可以表示为：
$$\left[\begin{array}{c}{\mathbf{X}}_1(t)\\ {\mathbf{X}}_2(t)\\ ⋮\\ {\mathbf{X}}_N(t)\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_1(t)+{\mathbf{S}}_2(t)+\dots +{\mathbf{S}}_M(t)+{\mathbf{N}}_1(t)\\ e^{-j2\pi \frac{d\sin {\theta }_1}{\lambda }}{\mathbf{S}}_1(t)+\dots +e^{-j2\pi \frac{d\sin {\theta }_M}{\lambda }}{\mathbf{S}}_M(t)+{\mathbf{N}}_2(t)\\ ⋮\\ e^{-j2(N-1)\pi \frac{d\sin {\theta }_1}{\lambda }}{\mathbf{S}}_1(t)+\dots +e^{-j2(N-1)\pi \frac{d\sin {\theta }_M}{\lambda }}{\mathbf{S}}_M(t)+{\mathbf{N}}_N(t)\end{array}\right]$$
其中，N是接收天线的数目，M是信号源数目。
实际处理中我们接收到的矩阵是一个复数方阵：不同行是不同接收天线，不同列是不同快时间采样点，包含了信号和噪声，如下：
$$\mathbf{X}(k)=\left[\begin{array}{cccc}{X}_1(1)& X_1(2)& \dots & X_1(k)\\ X_2(1)& X_2(2)& \dots & X_2(k)\\ ⋮& ⋮& \ddots & ⋮\\ X_N(1)& X_N(2)& \dots & X_N(k)\end{array}\right]$$

3、MUSIC具体算法

对阵列X做去均值处理，之后做相关处理得到协方差矩阵，这里，每一行是一个随机变量，得到其协方差矩阵【协方差矩阵的计算及意义_hi_linda的博客-CSDN博客_矩阵的协方差】
$${\mathbf{R}}_{XX}=\mathbf{E}[{\mathbf{XX}}^H]$$
其中，H表示复数矩阵的共轭转置。
$$\mathbf{X}(t)=\mathbf{A}(\theta )\mathbf{S}(t)+\mathbf{N}(t)$$
这里零均值化了，噪声均值认为为0，并且认为噪声和信号相互独立，从而得到：
$$\begin{array}{rl}{\mathbf{R}}_{XX}& =\mathbf{E}[(\mathbf{AS}+\mathbf{N})(\mathbf{AS}+\mathbf{N}{)}^H]\\ & =\mathbf{E}[(\mathbf{AS}+\mathbf{N})({\mathbf{S}}^H{\mathbf{A}}^H+{\mathbf{N}}^H)]\\ & =\mathbf{AE}[{\mathbf{SS}}^H]{\mathbf{A}}^H+\mathbf{E}[{\mathbf{NN}}^H]\\ & ={\mathbf{AR}}_S{\mathbf{A}}^H+{\mathbf{R}}_N\\ & ={\mathbf{AR}}_S{\mathbf{A}}^H+{\sigma }_N^2{\mathbf{I}}_N\end{array}$$
最后变成$N\times N$维矩阵。 $X$原来是N行k列矩阵。${\mathbf{R}}_N$ 是噪声相关阵，噪声的协方差矩阵。 ${\sigma }_N^2$是噪声方差，在实际应用中，我们通常无法直接得到 ，能用的只有样本的协方差矩阵：
$${\hat{\mathbf{R}}}_{XX}=\frac{1}{k-1}{\mathbf{XX}}^H$$
这是Rx的最大似然估计。 Plus：什么是最大似然估计？去概率论学习。采样点数N趋于无穷时，在统计上是一致的。
实际计算中：我们使用一个chirp，即一个发射的chirp被所有的接收天线接收（MIMO可等效），采样点数k，得到采样的矩阵为：

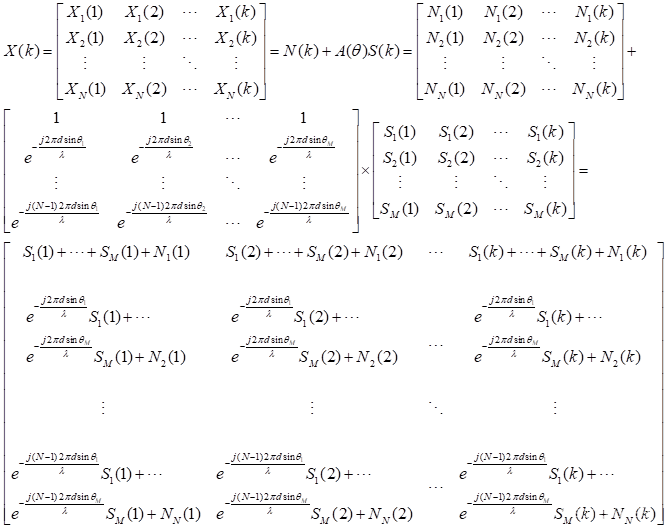
N行，N是接收天线数目；k列，k是采样点数。需要求解的是：通过对采样的输出信号X(k)，估计出M个信号源各自的波达方向角${\theta }_i(i=1,2,\cdots ,M)$。根据矩阵特征分解的理论，可对阵列协方差矩阵进行特征分解，首先考虑理想情况，即无噪声的情况：
$$\mathbf{A}(\theta )=\left[\begin{array}{cccc}1& 1& \dots & 1\\ e^{-j2\pi \frac{d\sin {\theta }_1}{\lambda }}& e^{-j2\pi \frac{d\sin {\theta }_2}{\lambda }}& \dots & e^{-j2\pi \frac{d\sin {\theta }_M}{\lambda }}\\ ⋮& ⋮& \ddots & ⋮\\ e^{-j2(N-1)\pi \frac{d\sin {\theta }_1}{\lambda }}& e^{-j2(N-1)\pi \frac{d\sin {\theta }_2}{\lambda }}& \dots & e^{-j2(N-1)\pi \frac{d\sin {\theta }_M}{\lambda }}\end{array}\right]$$
这里A是范德蒙矩阵，只要满足${\theta }_i\ne {\theta }_j,i\ne j$，则矩阵的各列相互独立。则：
$$\begin{array}{rl}{\mathbf{R}}_{XX}& =\mathbf{E}[{(\mathbf{AS})(\mathbf{AS})}^H]\\ & =\mathbf{AE}[{\mathbf{SS}}^H]{\mathbf{A}}^H\\ & ={\mathbf{AR}}_S{\mathbf{A}}^H\end{array}$$
又因为信号源两两不相关， S是M行k列矩阵；【引理：矩阵与其转置乘积的秩与矩阵原来的秩相等，怎么用多种方法证明，A矩阵的秩和A转置乘A的秩相等？ - 知乎 (zhihu.com) 】，因此$r({\mathbf{SS}}^H)=r(\mathbf{S})=M$，并且${\mathbf{R}}_S$为方阵，则 ${\mathbf{R}}_S$为非奇异矩阵，矩阵满秩，${\mathbf{R}}_S$可逆，特征值不为0，矩阵 ${\mathbf{R}}_S$的转置与矩阵拥有相同的特征值【为什么A可以逆，A转置乘以A正定？ - 知乎 (zhihu.com)】。且： 是正定矩阵，有M个正特征值证明如下：【这里貌似有点问题，待证明】

并且且${\mathbf{R}}_S$为厄米特矩阵【一个矩阵的共轭转置等于他本身，则这个矩阵是厄米特矩阵：证明：$({\mathbf{R}}_S{)}^H=({\mathbf{SS}}^H{)}^H=({\mathbf{SS}}^H)={\mathbf{R}}_S$】，他的共轭转置等于他本身，${\mathbf{R}}_S$的特征值都是实数。
引理：协方差矩阵是对称半正定矩阵【协方差矩阵(covariance matrix)是半正定的(positive semi-definite)证明_hitWeek的博客-CSDN博客_协方差矩阵半正定证明】，且矩阵相合不改变矩阵的秩【合同矩阵_百度百科 (baidu.com)】，因此 的秩与 的秩相同，都是M，引理：合同矩阵特征值正负个数相同【两个矩阵合同，这两个矩阵的特征值有什么关系么，_百度知道 (baidu.com)】，因此， 有M个正特征值，以及N-M个0特征值！
再看有噪声的情况。
$$\begin{array}{rl}{\mathbf{R}}_{XX}& =\mathbf{E}[(\mathbf{AS}+\mathbf{N})(\mathbf{AS}+\mathbf{N}{)}^H]\\ & =\mathbf{E}[(\mathbf{AS}+\mathbf{N})({\mathbf{S}}^H{\mathbf{A}}^H+{\mathbf{N}}^H)]\\ & =\mathbf{AE}[{\mathbf{SS}}^H]{\mathbf{A}}^H+\mathbf{E}[{\mathbf{NN}}^H]\\ & ={\mathbf{AR}}_S{\mathbf{A}}^H+{\mathbf{R}}_N\\ & ={\mathbf{AR}}_S{\mathbf{A}}^H+{\sigma }_N^2{\mathbf{I}}_N\end{array}$$
${\mathbf{R}}_{XX}$为满秩矩阵，所以有N个正实特征值(这里貌似有点问题，待证明)，且${\mathbf{R}}_{XX}$为厄米特矩阵【
$$\begin{array}{rl}({\mathbf{R}}_{XX}{)}^H& =(\mathbf{A}{\mathbf{R}}_S{\mathbf{A}}^H+{\sigma }_N^2{\mathbf{I}}_N{)}^H\\ & =\mathbf{A}({\mathbf{R}}_S{)}^H{\mathbf{A}}^H+{\sigma }_N^2{\mathbf{I}}_N\\ & ={\mathbf{AR}}_S{\mathbf{A}}^H+{\sigma }_N^2{\mathbf{I}}_N\\ & ={\mathbf{R}}_{XX}\end{array}$$
因此特征向量是正交的。有M个特征值是与信号和噪声都有关的，N-M个特征向量为噪声有关的。 ${\mathbf{R}}_S$是输入信号的协方差矩阵，是信号相关矩阵。${\mathbf{R}}_N$是噪声相关阵，噪声的协方差矩阵，协方差矩阵是对称半正定矩阵，${\sigma }_N^2$是噪声功率。
下面是论证特征值分解，特征子空间正交，矩阵正交分解
${\mathbf{R}}_{XX}$是厄米特矩阵，前M个特征值不相同，且均为正，后面N-M个特征值相同，均为噪声有关的特征值，因此【引理矩阵论：属于厄米特矩阵不同特征值的特征向量正交】
特征分解：将矩阵${\mathbf{R}}_{XX}$的特征向量按照信号和噪声分成两部分，前M个列向量为信号的特征值对应的特征向量，后面N-M个特征向量为噪声分量对应的特征向量。则有：

$${\mathbf{R}}_{XX}\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots {\mathbf{x}}_M,{\mathbf{x}}_{M+1},\cdots {\mathbf{x}}_N\right)=\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots {\mathbf{x}}_M,{\mathbf{x}}_{M+1},\cdots {\mathbf{x}}_N\right)\left(\begin{array}{ccccc}{J}_M& & & & \\ & {\lambda }_{M+1}& & & \\ & & \ddots & & \\ & & & & {\lambda }_N\end{array}\right)$$
前面信号的特征值不一定化为对角形，所以用J来表示了。
$${\lambda }_1⩾{\lambda }_2⩾...⩾{\lambda }_K>{\lambda }_{K+1}=...={\lambda }_M={\sigma }^2$$即前K个特征值与信号有关。特征子空间分解： $${\mathbf{R}}_{XX}\left(\begin{array}{cc}{P}_S& P_N\end{array}\right)=\left(\begin{array}{cc}{P}_S& P_N\end{array}\right)\left(\begin{array}{ccccc}{J}_M& & & & \\ & {\lambda }_{M+1}& & & \\ & & \ddots & & \\ & & & & {\lambda }_N\end{array}\right)$$
$$\begin{array}{rl}{\mathbf{R}}_{\mathrm{XX}}& =\left(P_S{P}_N\right)\left(\begin{array}{ccccc}{J}_M& & & & \\ & {\lambda }_{M+1}& & & \\ & & \ddots & & \\ & & & {\lambda }_N& \end{array}\right){\left(P_S{P}_N\right)}^{-1}\\ & =\left(P_{S}0\right)\left(\begin{array}{ccccc}{J}_M& & & & \\ & 0& & & \\ & & & \ddots & \\ & & & & 0\end{array}\right){\left(\begin{array}{cc}{P}_S& 0\end{array}\right)}^{-1}+\left(\begin{array}{cc}0& P_N\end{array}\right)\left(\begin{array}{ccccc}{J}_M& & & & \\ & {\lambda }_{M+1}& & & \\ & & \ddots & & \\ & & & & {\lambda }_N\end{array}\right){\left(\begin{array}{cc}0& P_N\end{array}\right)}^{-1}\end{array}$$
因此，进行特征子空间分解，由于特征向量正交，因此构成的特征子空间也是正交的，协方差矩阵${\mathbf{R}}_{XX}$可以进行特征值分解，利用特征向量构建两个正交的子空间，分别为信号子空间和噪声子空间 矩阵分解339
$$\begin{gathered} R_{XX}=U\Sigma U^H=U_S{\Sigma }_S{U}_S^H+U_N{\Sigma }_N{U}_N^H \\ U=[U_S,U_N],\Sigma =diag({\sigma }_1^2,\cdots {\sigma }_N^2) \end{gathered}$$
Us是由大的特征值构成的特征向量，成为信号子空间，Un是由小的特征值构成的特征向量，称为噪声子空间。
$$\Sigma =\left[\begin{array}{cc}{\Sigma }_S& \\ & {\Sigma }_N\end{array}\right]=\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_N\end{array}\right]$$
$${\lambda }_1⩾{\lambda }_2⩾\cdots ⩾{\lambda }_M>{\lambda }_{M+1}=\cdots ={\lambda }_N={\sigma }^2$$
$${\Sigma }_S=\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_M\end{array}\right]$$
$${\Sigma }_N=\left[\begin{array}{cccc}{\lambda }_{M+1}& & & \\ & {\lambda }_{M+2}& & \\ & & \ddots & \\ & & & {\lambda }_N\end{array}\right]$$
噪声子空间Un与信号子空间Us正交。因此将与信号个数M相等的特征值和对应的特征向量看做信号部分空间，将剩下的N-M个特征值和特征向量看做噪声部分空间。设λi是第i个特征值，vi是与λi相对应的特征向量，即：
$${\mathbf{R}}_{XX}{\nu }_i={\lambda }_i{\nu }_i$$
由矩阵的形式$$R_{XX}=A{R}_S{A}^H+{\sigma }^{2}I$$
可知，最后N-M个特征值均为 $${\lambda }_i={\sigma }^2$$
，是最小特征值，设特征向量为vi，带入可得：$$(A{R}_s{A}^H+{\sigma }^{2}I)v_i={\sigma }^2{v}_i$$
展开可得：
$$A{R}_s{A}^H{\nu }_i=0$$
因为$A^{H}A$是M*M维满秩矩阵，因此逆存在，而Rs满秩，因此逆存在，则上式两边同时乘以$R_s^{-1}{\left(A^{H}A\right)}^{-1}{A}^H$
可得：$$R_s^{-1}{\left(A^{H}A\right)}^{-1}{A}^{H}A{R}_s{A}^H{\nu }_i=0$$
因此：$A^H{\nu }_i=0,i=D+1,D+2,\dots ,M$
由上式可得，噪声对应的特征向量与矩阵A正交！而A的各列是与信号源的方向相对应的，因此可以利用噪声的特征向量求解信号源方向。
构造噪声矩阵$E_n=\left[\begin{array}{c}{\nu }_{M+1},{\nu }_{M+2},\dots ,{\nu }_N\end{array}\right]$
定义空间谱$$P_{mu}(\theta )=\frac{1}{a^H(\theta )E_n{E}_n^{H}a(\theta )}$$
其中
$$a(\theta )=\left(\begin{array}{c}1\\ e^{-j2\pi d\sin \theta /\lambda }\\ ⋮\\ e^{-j(N-1)2\pi d\sin \theta /\lambda }\end{array}\right)$$
当$\theta$恰好是某一个信号源角度时，因为正交性，$P_{mu}$有峰值。计算谱函数，通过寻求峰值来得到波达方向的估计值。

4、仿真+实测-待实现