线性分类基础（1）

1. 逻辑回归

1.1 两个基本点：

1. 名为 回归 实为 分类；
2. 是线性的分类器。

为啥有 回归？
该算法基于多元线性回归算法,.

1.2 一条曲线

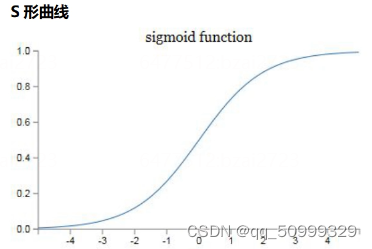
Sigmoid函数：
$$\begin{gathered} y=\frac{1}{1+e^{-x}} \\ y\in [0,1],x\in (-\infty ,+\infty ) \end{gathered}$$

# Python 实现 sigmoid 函数
import numpy as np
import math
import matplotlib.pyplot as plt


def sigmoid(x):
	a = []
	for item in x:
		a.append(1.0/(1.0 + math.exp(-item))
	return a


if __name__ == '__main__':
	x = np.arrange(-10, 10, 0.1)  # 在 (-10, 10) 之间每隔 0.1 取 一个数
	y = sigmoid(x)
	# 画出图形
	plt.plot(x, y)
	plt.show()

输出的图像:

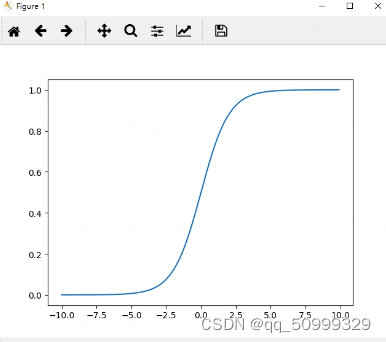
1.2.1 讨论一下 Sigmoid 的作用

该算法基于多元线性回归算法,
在其基础上把结果缩放到 0与1 之间,
以 0.5 为界限将结果分为两类，
越接近 1 为正例，越接近 0 为负例。
所以结合线性回归公式可以有:
$$y=\frac{1}{1+e^{-Z}}$$
$$Z={\theta }^{T}x$$

分类的本质
找分界处，则该分类器就是找0.5时 θ 的解，后续通过确定分界的 θ 分类数据。
sigmoid函数的原理
二分类，数学模型对应 伯努利分布，即 结果 有 0 和 1 两种，且两者概率和为1。
则其概率函数为
$$f\left(x|p\right)=\{\begin{array}{l}{p}^x{q}^{1-x},x=0,1\\ 0,x\ne 0,1\end{array}\left(q=1-p\right)$$
逻辑回归的sigmoid函数也就将 x 划分为正例1和负例0。

1.2.2 广义线性回归(由伯努利推Sigmoid)

不管是分类还是回归问题,
我们都是想预测 某个随机变量y，而 y 是某些特征 x 的 函数。
我们对这种情况会有三个基本假设:

1. 概率分布 服从 指数族分布；
2. 给出历史数据输入x，目的是得到预测函数结果 y 在 x 情况下的期望。
3. 参数 η 与 输入 x 是线性相关的： η = θx。

指数族分布
基本有:
高斯分布、二项分布、伯努利分布、多项分布、泊松分布、指数分布、beta分布、拉普拉斯分布、gamma分布。
如果 y 服从某个，就可以用广义线性回归进行建模。

指数族分布的模型公式：
$$\begin{gathered} p\left(y;\eta \right)=b\left(y\right)\exp \left({\eta }^{T}T\left(y\right)-a\left(\eta \right)\right) \\ \eta \text{是}\text{自然参数(我们要求解的模型)，}T\left(y\right)\text{是}\text{充分统计量}\left(\text{一般就为}y\right) \\ a\left(\eta \right)\text{是}\text{对数部分函数}\left(\text{确保分布的连续函数积分为}1\right) \end{gathered}$$
那么如何由 伯努利挂接sigmoid?

首先看伯努利分布:
$$\begin{gathered} p\left(y;\varphi \right)={\varphi }^y{\left(1-\varphi \right)}^{1-y} \\ =exp\left(ylog\varphi -\left(1-y\right)log\left(1-\varphi \right)\right) \\ =exp\left(\left(log\left(\frac{\varphi }{1-\varphi }\right)\right)y+log\left(1-\varphi \right)\right) \\ \varphi \text{为预测的期望，}y\text{为真实标签}\left(0\text{或}1\right) \end{gathered}$$

对应指数族分布模型,得出模型η:
$$\begin{gathered} \eta =Z=log\left(\frac{\varphi }{1-\varphi }\right) \\ {e}^Z=\frac{\varphi }{1-\varphi } \\ \varphi =e^Z-e^Z\cdot \varphi =\frac{1}{1+e^{-Z}} \\ \text{这样求出来就是}\text{预测的期望}\left(\text{或概率}\right),\text{也是}Sigmoid\text{的可见形态} \end{gathered}$$
至此转化完成。

然后你回看线性回归
高斯分布 -> η = ax + b
首先列出高斯分布，设置方差为1:
$$p\left(y;\mu \right)=\frac{1}{\sqrt{2\pi }}exp\left(-\frac{1}{2}{\left(y-\mu \right)}^2\right)$$
对应广义线性分布:
$$p\left(y;\mu \right)=\frac{1}{\sqrt{2\pi }}exp\left(-\frac{1}{2}{y}^2\right)\cdot exp\left(\mu y-\frac{1}{2}{\mu }^2\right)$$
则期望 μ 就为 η, 即 η = θx，而正好求期望μ。

1.3 损失函数

这里用到的还是最大似然估计 (MLE) 的思想,根据若干已知的X,y(训练集)找到一组 W， 使得 X 条件下 y 发生的概率最大。
逻辑回归预测的期望是 结果为 正例标签 的概率是多少，则模型的好解就是正确结果的概率越大越好，即:
$$P\left(\text{正确}\right)=\{\begin{array}{l}{h}_{\theta }\left(x\right),y=1\\ 1-h_{\theta }\left(x\right),y=0\end{array}$$
进一步整合:
$$P\left(\text{正确}\right)={\left(h_{\theta }\left(x\right)\right)}^y\cdot {\left(1-h_{\theta }\left(x\right)\right)}^{1-y}$$
则 P 越大越好，可以作为似然函数，然后对其取对数:
$$P\left(\theta \right)=\sum _{i=1}^m{y}^i\log h\left(x^i\right)+\left(1-y^i\right)\log \left(1-h\left(x^i\right)\right)$$
损失函数则为越小越好，取P的负数即可:
$$L\left(\theta \right)=-(\sum _{i=1}^m{y}^i\log h\left(x^i\right)+\left(1-y^i\right)\log \left(1-h\left(x^i\right)\right))$$

1.4 代码实现

import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
import numpy as np
import math


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def p_w_function(features, w):
    """
        线性关系 Z 的 Sigmoid 的 得分
    :param features: 数据特征
    :param w: 所得参数
    :return: Sigmoid得分
    """
    Z = np.dot(features, w.T)
    return sigmoid(Z)


def loss_function(y_hat, y):
    """
        计算 Loss 损失
    :param y_hat: 预测值
    :param y: 实际值
    :return: Loss 值
    """
    loss = -(np.dot(y, np.log(y_hat)) + np.dot((1 - y), np.log(1 - y_hat)))
    return loss


if __name__ == '__main__':
    # 读取数据
    data = load_breast_cancer()
    X, y = data['data'][:, :2], data['target']
    print(X.shape, y.shape)
    # 定义模型
    model = LogisticRegression(fit_intercept=False)  # 参数是: 是否计算W0
    model.fit(X, y)
    # 查看参数
    w = model.coef_
    print(w.shape)
    # 模拟参数
    w_space = np.linspace(w - 0.6, w + 0.6, 50)
    print(w_space.shape)
    # 计算得分和loss
    scores = np.array([p_w_function(X, W) for W in w_space])
    print(scores.shape)
    loss = np.array([loss_function(score.ravel(), y) for score in scores])
    # 看一下区别
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    fig = plt.figure(figsize=(10, 9))

    plt.subplot(2, 1, 1)  # 第一个参数 w1
    plt.plot(w_space.reshape(-1, 2)[:, 0], loss, label='loss')
    plt.xlabel('w1')
    plt.ylabel('loss')
    plt.title('w1 与 loss')
    plt.legend()

    plt.subplot(2, 1, 2)  # 第二个参数 w2
    plt.plot(w_space.reshape(-1, 2)[:, 1], loss, label='loss')
    plt.xlabel('w2')
    plt.ylabel('loss')
    plt.title('w2 与 loss')
    plt.legend()

    plt.show()

1.5 逻辑回归 求导

$$\begin{gathered} y^{‘}={\left(\frac{1}{1+e^{-Z}}\right)}^{\prime } \\ =\frac{1}{1+e^{-Z}}\cdot \left(1-\frac{1}{\left(1+e^{-Z}\right)}\right) \\ =y\cdot \left(1-y\right) \end{gathered}$$
损失函数求导:
$$\begin{gathered} L\left(\theta \right)\prime ={\left(-\frac{1}{m}\sum _{i=1}^m{y}_i\log h\left(x_i\right)-\left(1-y_i\right)\log \left(1-h\left(x_i\right)\right))\right)}^{\prime } \\ =\frac{1}{m}\sum _{i=1}^m\left(h\left(x_i\right)-y_i\right)x_i^j \end{gathered}$$

1.6 鸢尾花练习

1.6.1 鸢尾花练习（二分类）

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
import numpy as np

# 加载数据
iris = load_iris()
print(iris.keys())
# 转化标签 为 二分类问题 (以 是否第三种 为基准)
X, y = iris['data'], (iris['target'] == 2).astype(np.int_)
print(X.shape, y.shape)

# 模型定义
model = LogisticRegression(solver='sag', max_iter=1000)
model.fit(X, y)

# 新数据预测
X_new = np.linspace(0, 3, 1000).reshape(-1, 4)
print(X_new.shape)
y_hat_prob = model.predict_proba(X_new)  # 获取可能性
print(y_hat_prob)
y_hat = model.predict(X_new)  # 获取类别号
print(y_hat)

1.6.2 鸢尾花练习（多分类）

二分类 下的 多分类, one vs all， 即指定某一类为基准，其他为附属类，分别计算不同基准求最大概率下的类别。
逻辑回归处理多分类问题 会将 其转化为 多个 二分类问题。

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
import numpy as np

# 加载数据
iris = load_iris()
print(iris.keys())

# 多分类方式
# 转化标签 为 二分类问题 (以 是否第三种 为基准)
X, y = iris['data'], iris['target']
print(X.shape, y.shape)

# 模型定义
model = LogisticRegression(solver='sag', max_iter=10000, multi_class='ovr')
model.fit(X, y)

# 新数据预测
X_new = np.linspace(0, 3, 1000).reshape(-1, 4)
print(X_new.shape)
y_hat_prob = model.predict_proba(X_new)  # 获取可能性
print(y_hat_prob, y_hat_prob.shape)
y_hat = model.predict(X_new)  # 获取类别号
print(y_hat, y_hat.shape)