分解素因子，区间素数筛

素因子

重要知识：把一个数字进行质因数分解，可以得到它的因子数量等于 $\prod （a_i+1）$其中ai是第 i 个质数的幂次。

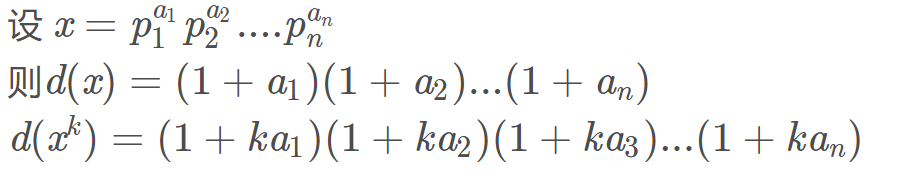
能分解出n个因子的最小正整数

https://codeforces.com/problemset/problem/27/E

所以每个质数的系数对因子数量贡献是等价的，因此，相同的因子数要想得到尽可能小的数字，肯定是小的质数次数比较大。又由于前16个质因数相乘已经大于1e18了，所以只考虑前16个质因数即可。由于数据范围很小，直接dfs选出每个质因数的次数，筛选出最小的结果即可。
由于ans要设置得大于1e18,一定要unsigned long long

#include <iostream>
#include <math.h>
using namespace std;
typedef  unsigned long long ll;//long long 过不了 

//最坏的情况，前16个质数的幂次都为1，那前16个数相乘也将超过1e18
int p[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53}; 
ll ans=1e18+5;
ll n;
void dfs(ll now,ll cnt,int pos){
	if(cnt==n){
		ans=min(ans,now);
		return ;
	}
	if(pos>=16)return;
	for(int i=1;i<=60;i++){//对于每个质因数取多少次 
		now*=p[pos];
//		cnt*=(1+i);
		if(now>1e18||cnt*(1+i)>n)break;//这条路走不通了
		dfs(now,cnt*(1+i),pos+1); 
	}
}
int main(){//能分解出n个因子的最小正整数n==(1+a1)*(1+a2)……
	 cin>>n;
	 dfs(1,1,0);
	cout<<ans;
	return 0;
}

整数的素因子分解

题目链接

一、 int范围的数分解素因子只可能用到30以内的素数, 共10个

const int N=30；
int prime[10];
int judge[N];

？？？很需要质疑啦
97532468=2^211171011291 可以分解出101这个质数耶，以后还是取最大数范围的开方值好了，素数分解的因子必定在其开放值范围内的（不在的必定是剩下的素数）long int 1e10,这里应取1e5
二、100以内的质数有: 2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。 一共有25个。”

三、由于前16个质因数相乘已经大于1e18了，所以longlong范围只考虑前16个质因数即可

法一、素数筛

#include <iostream>
#include <math.h>
using namespace std;
const int N=1e5;
typedef long long ll;
bool judge[N];
ll prime[N];
ll cnt;
ll expon[N];
ll bas[N];
ll len;
void oula(){
	for(int i=2;i<N;i++){
		if(!judge[i])prime[cnt++]=i;
		for(int j=0;j<cnt&&i*prime[j]<=N;j++){
			judge[i*prime[j]]=1;
			if(i%prime[j]==0)break;
		}
//		if(judge[i])continue;
//		prime[cnt++]=i;
//		for(int j=i*i;j<N;j+=i){
//			judge[j]=1;
//		}
	}
//	for(int i=0;i<cnt;i++){
//		cout<<prime[i]<<" ";
//	}
}
void factor(ll x){
	int s=(int)sqrt(x*0.1);
	for(int i=0;i<cnt&&prime[i]<=s;i++){
//		cout<<i<<" "<<prime[i]<<endl;
//	if(x%prime[i]!=0)continue;
	if(x%prime[i]==0){
		bas[len]=prime[i];
		expon[len]=0;
		while(x%prime[i]==0){
			x/=prime[i];
			expon[len]++;
		}
		len++;
}		
	}
	if(x!=1){
		bas[len++]=x;
		expon[len-1]=1;
	} 
}

int main(){
	ll x;
	cin>>x;
	oula();
	factor(x);
	cout<<x<<"=";
	if(x==1){
		cout<<"1";
		return 0;
	}
	for(int i=0;i<len;i++){
		if(expon[i]!=1)cout<<bas[i]<<"^"<<expon[i];
		else cout<<bas[i];
		if(i!=len-1)cout<<"*";
	}
	return 0;
}

直接试除整除，不用筛素数👍

#include <iostream>
#include <math.h>
using namespace std;
typedef long long ll;
void solve(ll x){
	int b,k;//基数、指数
	int s=x;
	int flag=false;
	for(int i=2;i<=s;i++){//s分解的质因子在sqrt(s)内,s是下一次要分解的整数 
	//这里i<s比i<sqrt(x)厉害多了！！！！！！！！
		b=k=0;
		if(s%i==0){
			b=i;
			while(s%i==0){
	//为啥不用判断是否i为质数，一定是，因为在i之前遇到的质数足以把s中的
	//因子i逐一分解掉，比如对于2，s连除2，所以4，8都是不能整除之后的s的 
				s/=i;
				k++;
			} 
		
			if(flag)cout<<"*";
			else flag=true;
			if(k==1)cout<<b;
			else if(k>1)cout<<b<<"^"<<k;
		}
	} 
}

int main(){
	ll x;
	cin>>x;
	if(x==1)cout<<"1=1";
	else {
		cout<<x<<"=";
		solve(x); 
	}
	
	return 0;
}

不知道为什么只有19分，感觉没错哇

#include <bits/stdc++.h>
using namespace std;
#define int long long int

const int N=1e6+5;
int cnt;//质因子个数
int num[N];//num[i]代表质因子prime[i]的幂次
int prime[N];//存放从2开始的所有的质因子
int n;
void fun(int x){
	for(int i=2;i*i<=x;i++){
		if(x%i==0){
			prime[cnt]=i;
			while(x%i==0){
				x/=i;
				num[cnt]++;
			}
			cnt++;
		}
	}
	if(x!=1){
		prime[cnt]=x;
		num[cnt]++;
	}
}
signed main(){
    scanf("%lld",&n);
    fun(n);
    int res=1;
     if(n==1){
     	cout<<"1=1";
     	return 0;
	 }
    cout<<n<<"=";
   
    for(int i=0;i<=cnt;i++){//n分解出来的所有质因子
    if(i)cout<<"*";
        if(num[i]==1)cout<<prime[i];
		else if(num[i]>1)cout<<prime[i]<<"^"<<num[i];
    }

    return 0;
}

素数区间筛

给定区间[L,R]，计算区间素数个数

http://oj.ecustacm.cn/problem.php?id=1087
1、注意右边界要取等号
2、注意素数筛不能考虑1筛去1，得自己手工筛去
3、埃氏筛法为了化简，对于素数i，筛去合数时，可以从$i\ast i$筛去（$i\ast (2->i-1)这些数，通过2->i-1筛去了$ ），比从$i\ast 2$筛去，重复筛一个数的概率变小，但从i*i开始就要考虑数组越界问题，$j$一上来就等于$i\ast i$,而只要$j\ast j<=R$ 就可以去访问

#include <iostream>
#include <math.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;//1e12，
bool prime_sqrt[N];
bool prime[N];
ll sieve(ll L,ll R){
	ll res=0;	
	for(ll i=2;(ll)i*i<=R;i++){
	//埃氏筛法筛出[2,sqrt(R))的同时，把他的倍数从[L,R]筛去 
	   if(!prime_sqrt[i]){
	   		for(ll j=(ll)i*i;i<=1000&&(ll)j*j<=R;j+=i){//i不加上这个条件会数组越界 
//埃氏筛法所有形式对于素数i，都可以从i*i开始筛去合数，包括下面的st=max((ll)2*i,st);
//但是一定要逐一i*i可能导致数组越界，可以直接把i<=1000换成j<N
	   			prime_sqrt[j]=1;
			}
//方法一：
//			ll st=L;//i是素数，至少从i的两倍开始筛 
//			if(L%i!=0)st=(L/i+1)*i;
// //到这里st保底是是i的一倍，但i是素数，至少从2*i开始筛合数，还要加上下一句
//			st=max((ll)2*i,st);
//方法二：一句，减一是为了防止L本来就是i的倍数
			ll st=max(i,(L+i-1)/i)*i;//i=2 L=5 6
			for(ll j=st;j<=R;j+=i){
				if(prime[j-L])continue;//可能会重复筛一个数不能回回计数 
				prime[j-L]=1;
				res++;
			}
	   } 	
	}
	if(L==1)res++;//1不是素数，筛去 
	return R-L+1-res;
}
int main(){
	ll L,R;
	cin>>L>>R;
	cout<<sieve(L,R);;
	return 0;
}

#include <iostream>
#include <math.h>
#include <string.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;//1e12，
int prime_sqrt[N];
int prime[N];
void sieve(ll L,ll R){
//	memset(prime,0,sizeof(prime));
//	memset(prime_sqrt,0,sizeof(prime_sqrt));	
	for(ll i=2;(ll)i*i<=R;i++){
	//埃氏筛法筛出[2,sqrt(R))的同时，把他的倍数从[L,R]筛去 
	   if(!prime_sqrt[i]){
	   		for(ll j=i*2;j<N&&(ll)j*j<=R;j+=i){
	   			prime_sqrt[j]=1;
			}
//法一：
		ll st=L;//i是素数，至少从i的两倍开始筛 
		if(L%i!=0)st=(L/i+1)*i;
//到这里st保底是是i的一倍，但i是素数，至少从2*i开始筛合数，还要加上下一句
	st=max((ll)2*i,st);
			//ll st=max(2ll,(L+i-1)/i)*i;//i=2 L=5 6
			//2ll表示2是longlong 类型
			for(ll j=st;j<=R;j+=i){
				prime[j-L]=1;
			}
	   } 	
	}
}
int main(){
	ll L,R;
	cin>>L>>R;
	sieve(L,R);
	ll res=0;
	for(int i=0;i<R-L+1;i++){
		if(!prime[i])res++;
	}
	if(L==1)res-=1; 
	cout<<res;
	return 0;
}

Counting Divisors （HDU - 6069）

In mathematics, the function $d(n)$ denotes the number of divisors of positive integer nn.

For example, $d(12)=6$ because $1,2,3,4,6,12$ are all 12’s divisors.

In this problem, given $l,r$ and $k$ , your task is to calculate the following thing :
${\sum }_{L<=i<=R}d(i^k)mod998244353$

 Input 

The first line of the input contains an integer $T(1\le T\le 15)$, denoting the number of test cases.

In each test case, there are 33 integers $l,r,k(1\le l\le r\le 10^{12},r-l\le 10^6,1\le k\le 10^7).$

 Ouput 

For each test case, print a single line containing an integer, denoting the answer.

Sample Input

3
1 5 1
1 10 2
1 100 3

Sample Output

10
48
2302

求L~ R这所有数的k次幂 能分解出来的因子数之和
$x=L，L+1，L+2\cdots ,R$
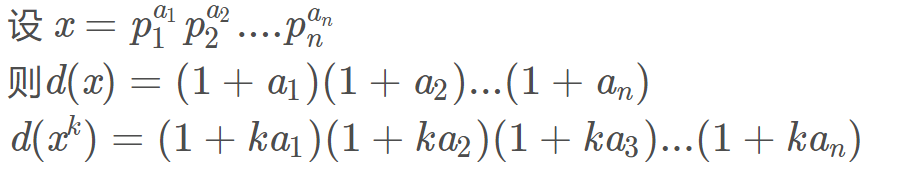$x的因子总数d(x)等于x能分解成的(各质因数幂次+1)的乘积$
$12=2^2\ast 3^1$
$d(12)=(1+2)\ast (1+1)=6$
求 ${\sum }_{L<=i<=R}d(i^k)mod998244353$

因$x<=10^{12}$，故可以考虑枚举出$10^6$以内的素数，采用区间素数筛求出每一个数的质因数指数
1 2 3 4 5
10
1 2 2 3 2

#include <iostream>
using namespace std;
typedef long long ll;
const int mod=998244353;
const int N=1e6+5;//1e12，一个合数x分解出来的质因子不可能大于sqrt(x)
int judge[N];
int prime[N];
int cnt; //以上线性筛
ll val[N];//存放L~R各数分解后的情况，等于1说明分解完毕，
//最后不为1说明剩个大于sqrt(R)的质数 
int ans[N];//存放L~R各数目前得到的因子个数ans[i]*=(1+k*res),res是对一个质数的分解幂次
 
void oula(){
	judge[0]=judge[1]=1;//1表示不是质数 
	for(int i=2;i<N;i++){
		if(!judge[i])prime[cnt++]=i;
		for(int j=0;j<cnt&&prime[j]<=N/i;j++){
			judge[i*prime[j]]=1;
			if(i%prime[j]==0)break;
		}
	}
}
void solve(ll L,ll R,ll k){
	for(ll i=L;i<=R;i++){
		val[i-L]=i; //不从下标0放放不下 ，R-L规定方位是N 
		ans[i-L]=1;
	}
	for(int i=0;i<cnt&&prime[i]<=R;i++){
		int now=prime[i];//遍历L-R,看对于质数now至多能分解出多少幂次
		ll st=L;//为了优化，因从第一个能分解出now的数开始                                     
		if(L%now!=0)st=(L/now+1)*now;
		for(ll j=st;j<=R;j+=now){
			ll res=0;
			while(val[j-L]%now==0){
				res++;
				val[j-L]/=now;
			}
			ans[j-L]=ans[j-L]%mod*(1+k*res)%mod;
		} 
	}
	for(ll i=L;i<=R;i++){
		if(val[i-L]!=1)ans[i-L]*=(1+k*1);//剩一个没分解的质数咯 
	} 
	ll sum=0;
	for(ll i=L;i<=R;i++){
		sum=(sum+ans[i-L])%mod;
	} 
	cout<<sum<<endl;
}
int main(){
	int n;
	cin>>n;
	ll L,R,k;
	oula();
	while(n--){
		cin>>L>>R>>k;
		solve(L,R,k);
	}
	return 0;
}

对于$1\le l\le r\le 10^{12}$筛出1e6范围的质数

//当x不是质数，必定存在两个约数，一个大于sqrt(x),一个小于sqrt(x)

bool isprime(int x){
	int e=(int)sqrt(x*1.0);
	for(int i=2;i<=e;i++){
		if(x%i==0)return false;
	}
	return true;
}

要求所有数L~R的质因子情况（质数就是1和本身，对于合数一定可以分解成

若干个质因数幂次的乘积，只需要筛出$sqrt(R)$以内的所有质数，
所有数分解的质因子要么在筛出的质数里，要么是不能再进行分解的最后质因子

$对任一x(L<=x<=R),$
情况1: x原本为质数 或 x约去一系列质数之后得到最后的质数
$ans\ast =(1+k\ast 1)$
情况2:x为合数 ,可以分解一个约数$x1<sqrt(x)<=sqrt(R),$令一个约数
x2>sqrt(x),若x2<sqrt( R),分解的一系列质因子都在筛出的素数里
若$x2>sqrt(R)$,重复以上操作,若x2经多次分解出的质因子都在晒出的素数里ok
若不在，即有约数>$sqrt(R)$，那该约数一定是质数，不用再进行分解转情况一
因为若该大于$sqrt(R)$的约数是合数，那么一定能分解出小于$sqrt(R)$的约数

找出大于1e6的最小质数？