文远知行杯广东工业大学第十六届程序设计竞赛(题解)

文远知行杯广东工业大学第十六届程序设计竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ

A:思维题

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e4 + 10;
ll n,m,l,r;
ll s[N][N];
int main()
{
    scanf("%lld%lld",&n,&m);
    if(n == 1 || n == 2)
    {
        while (m--)
        {
            cout<<0<<endl;
        }
         
    }else{
        while (m--)
        {
           scanf("%lld%lld",&l,&r);
           if(l == r)
           {
               cout<<n%l<<endl;
               continue;
           }
           else{
              for(int i = 2 ; i <= n; i++)
              {
               ll mid = ((n) / i) + 1;
               if(l <= mid && r >= mid)
               {
                   cout<<n%mid<<endl;
                   break;
               }else if(l > (n/i + 1))
               {
                   cout<<n % l<<endl;
                   break;
               } 
              } 
            }
        } 
    }
    return 0;
}

A题 题意：一共用n个数，从a[1] = n % 1 a[2] = n % 2 …… a[n] = n % n 再给定一个区间问该区间里的最大值 eg: n = 14 14 - 1 * 14 14 - 2 * 6 14 - 3 * 4 14 - 4 * 3 14 - 5 * 2 14 - 6 * 2 14 - 7 * 2 14 - 8 * 1 14 - 9 * 1 14 - 10 * 1 14 - 11 * 1 14 - 12 * 1 14 - 13 * 1 14 - 14 * 1 发现一个规律 14 6 4 3 2 2 2 1 1 1 1 1 1 1 0 2 2 2 4 2 0 7 6 5 4 3 2 1 n会在(n/2+1,n)范围内递减 同理(n/3+1,n/2)范围内也是递减 （n/4+1,n/3)递减 （n/n+1,n/n-1）递减 从第一个开始 n % i 可以看成 n - i * x a[1] = n - 1 * x a[2] = n - 2 * x …… a[n] = n - n * x（这里x取n*x最接近n的情况） x由n=0开始到n结束，当i * 2 = n时下一步边无法乘2，只能乘以1便会出现一个极大值 同理，当i * 3 = n时，下一步无法乘3，只能乘2也会出现一个极大值

F：数论题

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
typedef long long LL;
int main()
{
    int T;
    cin >> T;
    while(T -- ) {
       int n;
       cin >> n;
       int p, c, ans = 1;
       while(n -- ) {
           cin >> p >> c;
           int z = ((LL)c * 2 + 1) % mod;
           ans = ((LL)ans * z) % mod;
       }
       printf("%d\n", ans);
    }
 return 0;
}

F:题意 输出一组p和c 其中p为质数 求 pow(p1,i1) * pow(p2,i2) * pow(p3,i3) + ……+pow(pn,in) = x 求其中多少对互质 eg 2 * 2 + 1 * 3 = 12 {(1, 1),(1, 2),(1, 3),(1, 4),(1, 6),(1, 12),(2, 1),(2, 3),(3, 1),(3, 2),(3, 4),(4, 1),(4, 3),(6, 1),(12, 1)共15对} 定理：一个大于1的正整数均可以由若干个质数相乘 所以 所给的p和c就是x被分解为质因数的情况 由质数和其不包含其的数是互质 当p1,c1,p2,c2 （1 * (c1+1)(c2+1)）+ (c1 * (c2+1)) + (c2 * (c1+1))+ (c1* c2 * 1) = (c1 + 1 + c1)(c2 + 1) + (c2 * (c1+1+c1)) = (2c1 + 1)(2c2 + 2) 对于p1,c1,p2,c2 (1 * (c1+1)(c2+1)(c3+1)) + (c1 * (c2+1)(c3+1)) + (c2 * (c1+1)(c3+1)) + (c3 *(c1+1)(c2+1)) + (c1 * c2 * (c3+1)) +(c1 * c3 * (c2+1)) + (c2 * c3 * (c1+1)) + (c1 * c2 * c3 * 1) = (c3 + 1 + c3) {（1 * (c1+1)(c2+1)）+ (c1 * (c2+1)) + (c2 * (c1+1))+ (c1* c2 * 1)} =(2c3 + 1)(2c2 + 1)(2c3 + 1)

I题：贪心的dp问题

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000005;
int n, m, k;
int a[N];
ll dp[N][2];

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = k + 1; i <= n; i++)
    {
        dp[i][0] = max(dp[i - k][0], dp[i - k][1]);//这个不选等于上一个不选，上上个选，或者上一个选，上上个不选
        dp[i][1] = dp[i - k][0] + a[i] + a[i - k];//选这个等于（上一个不选）选这个
      //cout << dp[i][0] << " " << dp[i][1] << endl;//选这个和不选这个
    }
    ll ans = 0;
    for (int i = n - k + 1; i <= n; i++)//1 3 5 7 …… 2n + 1 这些点都会因为前一个受不受影响而改变，所以ans可以加上每一段不互不影响的
    {
        //cout<<dp[i][0]<<" "<<dp[i][1]<<endl;
        ans += max(dp[i][0], dp[i][1]);
    }    
    cout << ans;
    return 0;
}

I题题意：钩子长度为k 可以同时抓取两个（i，i+k），但不能只抓取一个， 核心：其影响了谁，求取互不影响的几组

影响因素上取分析 当 i i + k 当存在i + 2k时你便要分析取i i+k，还是i+k i+2k 所以你用数组dp进行dp [i ,1]表示该点取，那么它dp[i,1] = dp[i - k , 0] + a[i] + a[i - k]; dp[i , 0] = max(dp[i , 1] + dp[i,0]) 所以最后可以进行对最后一组(n - k + 1 , n)对这几组可以互不影响的几组数据进行相加，从而求取最大值

E： 前缀和dp问题

#include<bits/stdc++.h>
#define IOS std::ios::sync_with_stdio(false);
#define tcase int ttt;scanf("%d",&ttt);while(ttt--)
typedef long long ll;
using namespace std;
const ll N = 2e5+9;
const ll inf = 1e16;
const ll mod = 1e9+7;
int mx[N];
int pre[20][N];
char s[N];
int n;
void pro(){
	int sum = 0;
	for(int i = 1 ; i <= n ; i++){  //对从i开始的10步走法之内
		sum = 0; // 用于计数，表示该位置能走到且为声明值为0
		for(int j = i ; j <= i + 9 && sum >= 0 ; j++) //小于9步且生命值不能为0
        {
			if(s[j] == '0') sum--;
			else sum++;
			if(sum == 0)
            {
				pre[(j-i+1)][i] = 1; //存在从i走j-i+1步这种情况
			}
		}
	}
    for(int i = 1 ; i <= 10 ; i++)
    {
		for(int j = 1 ; j <= n ; j++)
        {
			pre[i][j] = pre[i][j] + pre[i][j-1]; 
            //前缀和  加上上一个点走了这些距离，如果pre[i][r-i+1]>pre[i][l-1]说明从l到r中多除了一些个这些距离的方案
		}
	}
}
int main(){
	scanf("%d",&n);
	scanf("%s",s+1);
	pro();
	int q;
	scanf("%d",&q);
	while(q--){
		int l,r;
		scanf("%d %d",&l,&r);
		int i;
		for(i = 10 ; i >= 1 ; i--)//从最大的开始遍历
        {     
			if(r - i + 1 >= l - 1)//保证步数位于l到r之内
            {  
				if(pre[i][r-i+1] - pre[i][l-1])//如果从r-i+1走i步大于从l-1走i步，说明存在这种情况
                {                              //要不就是从某个位置到r，要不就是从l到某个位置，或者从某个位置到某个位置
					break;
				}	
			}
		}
		printf("%d\n",i);
	}
	return 0;
}

  思路：dp[i,j] 表示从j走i个距离的情况是否存在（因为i<=10） 预先处理所有情况从任何一个位置走i步情况是否存在 对所有i步的情况进行前缀和处理 对于所给的l和r dp[i,r-i+1] > dp[i,l-1] 说明一件事说明能走i步的情况在l到r的位置存在，因为是相加，所以存在时，那么一定会大于dp[i.l-1]

J：构造函数(纯公式推导)

#include<bits/stdc++.h>

using namespace std;

const int MOD = 1e9 + 7;

int mpow(int x , int y = MOD - 2) {
    int ret = 1;
    while (y) {
        if (y & 1) ret = 1ll * ret * x % MOD;
        x = 1ll * x * x % MOD;
        y >>= 1;
    }
    return ret;
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(0);

    int N , m;
    cin >> N >> m;

    int u = m + N;

    int sum = 0;
    for (int i = 1 ; i <= N ; i++) {
        int x;
        cin >> x;
        sum += x;
        if (sum >= MOD) sum -= MOD;
    }

    if (m + N < N + sum) {
        cout << "0\n";
    } else {
        int ans = 1 , d = 1;
        for (int i = 1 ; i <= N + sum ; i++) {
            ans = 1ll * ans * (u - i + 1) % MOD;
            d = 1ll * d * i % MOD;
        }
        d = mpow(d);
        cout << 1ll * ans * d % MOD << endl;
    }
    return 0;
}

题意：

 

eg 3 5 n = 3 m = 5 A : 1 2 1 B：2 1 2 1 2 1 2 2 1 1 3 1 2 + 1 + 2 + 3 = 8 想法： 题目要求累积的累加 ， 累积我们可以看成一个卷积

 

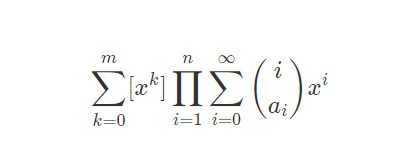
k我们代表 0 ，1， 2，3…… m f(x) = b0x^0 + b1x^1 + b2 x^2 + ……+ bk x^k 这时候这个构造函数我们只需要将b0 + b1 + b2 + b3 + b4 +……+ bk的和 上满那个例子 b0 = 0 b1 = 0 b2 = 0 b3 = 0 b4 = 1 b5 = 2 + 2 + 3 = 7

现在我们需要求对应的b0 b1 b2 b3 b4 b5 对A中的ai进行牛顿二项式构造 m代表正无穷 C(i , a0) f(x) = C(0,a0) x^0 + C(1,a0) x^1 + C(2,a0) x^2 + …… +C(n,a0)x^m C(i , a1) f(x) = C(0,a1) x^0 + C(1,a1) x^1 + C(2,a1) x^2 + …… +C(n,a1)x^m C(i , a2) f(x) = C(0,a2) x^0 + C(1,a2) x^1 + C(2,a2) x^2 + …… +C(n,a2)x^m …… C(i , an) f(x) = C(0,an) x^0 + C(1,an) x^1 + C(2,an) x^2 + …… +C(n,an)x^m 这里用卷积可以求出对应 x^0 x^1 x^2 x^3 x^4 …… x^k

对于该例子： (C(0,a0) * C(0,a1) * C(0,a2)) x^0 + (C(1,a0) * C(0,a1) * C(0,a2) + C(0,a0) * C(1,a1) * C(0,a2) + C(0,a0) * C(0,a1) * C(1,a2) ) x^1 + () x^2 同理 因为前面都为0所以我们直接来写x^5的情况

a0 = 1 a1 = 2 a2 = 1

5 0 0 0 5 0 0 0 5 4 1 0 4 0 1 0 4 1 1 4 0 1 0 4 0 1 4 3 2 0 3 0 2 0 3 2 2 3 0 2 0 3 0 2 3 …… 其实写了这些你会发现基本都为0 所以我们写出几个不为0的情况 2 2 1 1 3 1 1 2 2 其余情况均为0

(C(2,a0) * C(2,a1) * C(1,a2) + C(1,a0) + C(3,a1) + C(1,a2) + C(1,a0) * C(2,a1) * C(2,a2)) x^5 里面为7

所以我们便可以生成一个构造函数（说白了k就是在后面生成的构造函数中截取了一段）

 

上面公式推导中p = ai + 1 中 1/(1 - x) ^ p = 1/(1 - x) ^ai +1 = (ai + i , ai) x^i 和我们要的(i,ai)不同 这里i代表C(i , ai)中的i，方便卷积后直接取1到k的和，所以我们强行乘以ai以方便以后求和 (ai + i , ai) x^i * x^ai;

这样做不会有漏掉的，因为i从0开始 i+ai从ai开始，因为C(i,ai)中i大于等于ai才会不为0，其余均为0，所以不会出现漏掉的情况

然后求前k个ai的和，a1+a2+a3……+ ak-1+ak 因为最后推出式子为(k + t + n - 1 , n + t - 1) x^(k+t) 因为我们要找0到k，所以k+t = x 我们找x从0到k (x + n - 1 , n + t - 1) 这里就属于换元了，和下面的一样

 

在最后一步操作就是单纯的换元，在该题，无法采用换元，因为i和i+ai中i为同一个所以我们换也始终多ai 所以我们直接乘以x^ai得到 以后我们要找的x^k 前的ak了

 

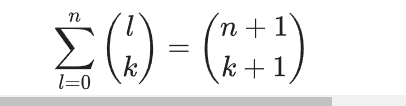
这里解释对最后一步求b1+b2+b3+……+bk的和 k = 0~m (k+n-1,n+t-1) = (m + n - 1 + 1 , n+t-1+1) = (m+n,n+t) (对于L的变换只进行自变量，对于k的变换为全部的常量)