常见的解题算法
1.求矩阵中子矩阵元素和不大于K的个数
前缀和+双指针O(n^3)
思路:
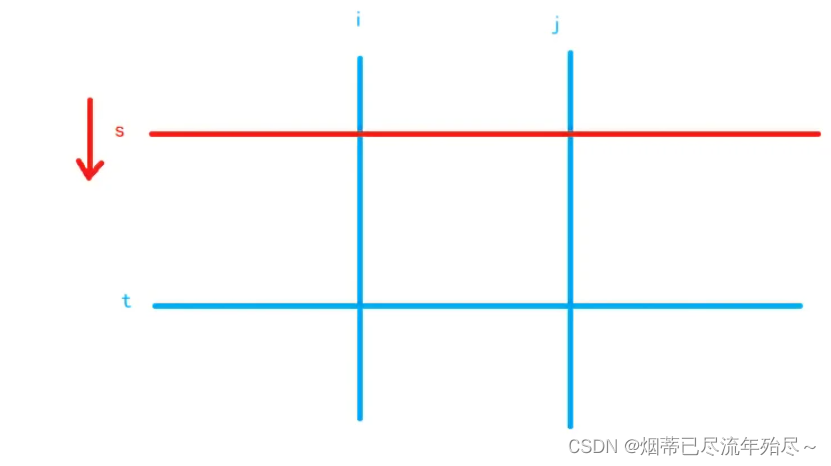
1)枚举子矩阵的 左边界i 和 右边界j,
2)用快指针t枚举子矩阵的下边界,慢指针s维护子矩阵的上边界 (s≤t)
3)如果得到的子矩阵的权值和大于 k,则慢指针s 前进,而子矩阵和必将单调不增,慢指针s 继续前进(如图),直到子矩阵的和不大于k,慢指针没必要前进了,因为该子矩阵的所有宽度为 j - i + 1的子矩阵(总共 t - s + 1种)一定满足要求,更新该情况对答案的贡献 t - s + 1;反之,如果慢指针s越界(s > t),则不操作,直接进入下层循环
#include<iostream>
using namespace std;
typedef long long ll;
const int N = 5e2+3;
int n, m, k;
int a[N][N]`
int main(){
ios::sync_with_stdio(false);
cin >> n >> m >> k;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
cin >> a[i][j];
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
}
}
ll ans = 0;
for(int i=1; i<=m; i++){
for(int j=i; j<=m; j++){
for(int s = 1, t = 1; t <= n; t ++ ){
while(s <= t && a[t][j] - a[s - 1][j] - a[t][i - 1] + a[s - 1][i - 1] > k) s ++ ;
if(s <= t) ans += t - s + 1;
}
}
}
cout << ans << '\n';
}
2.求字符串中某条件子串的个数
前缀和+哈希

思路:
1.求条件子串的个数,也就是求字符串的前缀和中满足条件子串的个数。 因为任意两个符合条件的·前缀和子串相减就是题目要求的子串。
2. 每种前缀和状态下的个数用哈希来维护,即undered_map
3. 需要构造一些结果,使出现0,1,2三种字符能得到不同但是互补的结果。
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define pb(x) push_back(x)
#define eb(x) emplace_back(x)
#define PII pair<int,int>
#define endl '\n'
#define fi first
#define se second
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
typedef long long LL;
const int maxn=4e5+10;
const int N=1e6+10;
const int mod=1e9+7;
void solve(){
int n; cin>>n;
string s; cin>>s;
LL ans=0;
map<PII,int>mp;
PII v=make_pair(0,0);
mp[v]=1; //初始化,最开始三个数都为0的前缀和状态有1个
//接下来遍历前缀和的0,1,2个数
for(int i=0;i<n;i++){
if(s[i]=='0') v.fi++, v.se++;
else if(s[i]=='1') v.fi--;
else v.se--;
ans+=mp[v];
mp[v]++;
}
cout<<ans<<endl;
}
int main(){
IOS;
int t; cin>>t;
while(t--){
solve();
}
return 0;
}
3.概率与期望DP

思路:
这道题要注意一定要保证游戏能够买到。如何在最优的情况下保证能够买到游戏,正面考虑太复杂了,我们倒着考虑,创建一个数组f用来记录,从第i开始到最后的最优的期望,对于f[n]也就是最后一天,马上就要停止发售了,所以必须要购买,所以这天的期望是0.5a+0.5b,那么对于一般的情况,例如i,我们已经知道了从i+1天开始购买的最佳的期望f[i+1],如何算出从第i天开始的最佳的期望,如果说,第i天不管购买a还是b都是不如之后购买的期望,那么f[i]=f[i+1],如果说第i天不管购买a还是购买b都是比之后购买要更好,那么肯定不会选择再之后购买,所以最好的期望就是0.5a+0.5b,如果说a<f[i+1]< b的话,这个时候我们为了追求利益最大话,有1/2的概率价格为a,还有1/2概率价格为b,当价格b的时候不如后面买的期望,为了使得期望更小我们选择后面买,注意价格是每天最早就公布了,所以我们是知道价格然后进行决策的。此时f[i]=0.5a+0.5f[i+1]。以此类推可以得到第一天决策的最佳期望。
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define endl '\n'
#define fi first
#define se second
#define pb(x) push_back(x)
#define PII pair<int, int>
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long LL;
const int maxn=1e5+10;
const int N=1e6+10;
const int mod=1e9+7;
int n;
double a[maxn], b[maxn];
double f[maxn];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
f[n] = 1.0*(a[n]+b[n])/2;
for(int i=n-1;i>=1;i--){
if(a[i]>=f[i+1] && b[i]>=f[i+1]) f[i]=f[i+1];
else if(a[i]<=f[i+1] && b[i]<=f[i+1]) f[i]=1.0*(a[i]+b[i])/2;
else{
if(a[i]>b[i]) swap(a[i],b[i]);
f[i]=1.0*(a[i]+f[i+1])/2;
}
}
printf("%.6lf\n",f[1]);
}
int main(){
int t; cin>>t;
while(t--){
solve();
}
}
4.数论
结论:如果a,b均是正整数且互质,则由ax+by, x>=0, y>=0不能凑出得最大数为ab-a-b.
5.求树的直径
树形dp O(n)
思路:
- 用 d[ ] 数组维护以i为根节点所能到达的最长距离,f[ ] 数组维护以i为根节点所能到达的最长距离,最终树的直径便为max(f[1], f[2], …, f[n]).
- d[ ]数组的状态转移方程:d[u] = max(d[u], d[v]+w).其中v是u的子结点,w是边{u,v}的边权;若是边权w可以为负值,那么:d[u] = max(max(d[u], d[v]+w), 0).
- f[ ]数组的状态转移方程: f[u]=max(f[u],d[u]+d[v]+w).其中v是u的子节点,经过结点u的树的直径也就是以u为结点所能到达的最大距离和次大距离之和;若是边权w可以为负值,那么:f[u]=max(f[u],max(d[u]+d[v]+w, d[u])).
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define INF 0x3f3f3f3f
#define fi first
#define se second
#define pb(x) push_back(x)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define PII pair<int,int>
typedef long long LL;
const int maxn=5e5+10;
const int N=1e7+10;
const int mod=1e9+7;
int n, ans;
int d[maxn],f[maxn]; //d[i]表示以i为根节点所能到达的最长距离, f[i]表示经过i结点的最大树直径
bool vis[maxn];
vector<PII>g[maxn];
void dfs(int u){
vis[u]=true;
int len=g[u].size(), v, w;
for(int i=0; i<len; i++){
PII node=g[u][i];
v=node.fi; w=node.se;
if(!vis[v]){
dfs(v);
//边权值为正的情况
// f[u]=max(f[u],d[u]+d[v]+w);
// d[u]=max(d[v]+w, d[u]);
//边权值可以为负数的情况
f[u]=max(f[u],max(d[u]+d[v]+w, d[u]));
d[u]=max(max(d[v]+w, d[u]), 0);
}
}
}
void solve(){
memset(vis,false,sizeof(vis));
cin>>n;
int u,v,w;
for(int i=1;i<n;i++){
cin>>u>>v>>w;
g[u].push_back({v,w});
g[v].push_back({u,w});
}
dfs(1);
for(int i=1; i<=n; i++) ans=max(ans, f[i]);
cout<<ans<<endl;
}
int main(){
IOS;
int t;
t=1;
while(t--){
solve();
}
return 0;
}
6.求分数是否是无限循环小数, 并求出最小的循环节长度
思路:
给定分数 p / q, 根据数学原理,一个分数可以表示为有限小数或无限循环小数。对于无限循环小数而言,循环节是必然存在的。通过欧拉函数和模运算,可以计算出循环节的长度。同时,通过化简分母为最简形式以及判断分数是否为有限小数,可以提前排除掉一部分情况,减少计算量。
- 首先判断给定的分数是否为有限小数。如果分母能够被2或5整除,则说明分数是有限小数,直接输出-1。
- 将分母化简为最简形式,并计算分母中包含2和5的个数,用c2和c5表示。
- 计算欧拉函数phi(q),得到与q互质的小于等于q的正整数个数。
- 遍历phi(q)的所有因子i,判断10 ^i和 10 ^(phi(q)/i)在模q下是否为1,如果是则更新循环节长度minn为i或phi(q)/i的较小值。
- 输出max(c2, c5)作为循环节前面部分的长度,输出minn作为循环节的长度。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
// 欧拉函数
int phi(int x) {
int res = x;
for (int i = 2; i <= x / i; i++) {
if (x % i == 0) {
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
}
if (x > 0) res = res / x * (x - 1);
return res;
}
LL qpow(LL a, LL b, int mod) {
LL res = 1;
while (b)
{
if (b & 1) res = res*a%mod;
a =a*a%mod;
b >>= 1;
}
return res;
}
// 求最大公约数
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
int main() {
LL p, q;
cin >> p >> q;
LL temp = gcd(p,q);
q /= temp;
p /= temp;
int c2 = 0, c5 = 0;
while (q % 2 == 0) q /= 2, c2++;
while (q % 5 == 0) q /= 5, c5++;
// 判断是否为有限小数
if (q == 1) {
cout << -1;
return;
}
int te= phi(q); //欧拉函数求出的te就是循环节的长度,但是不一定是最小的循环节长度
int minn = 1e18;
for (int i = 1; i <= te/ i; i++) {
if (te% i == 0) {
if (qpow(10, i, q) == 1) minn = min(minn, i);
if (qpow(10, te/ i, q) == 1) minn = min(minn, te/ i);
}
}
cout << max(c2, c5) << ' ' << minn;
return 0;
}






















 1904
1904











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










