贝叶斯神经网络

贝叶斯神经网络 及概率论基础知识

参考链接：
[1]贝叶斯神经网络----从贝叶斯准则到变分推断
[2]联合概率及其分布、边缘概率及其分布、条件概率及其分布和贝叶斯定理
[3]【深度学习：从入门到放弃】一文让你完全搞明白重参数化是怎么回事，轻松掌握原理和应用！
[4]机器学习_KL散度详解（全网最详细）
最近在阅读刘三女牙老师智慧教育相关的论文的时候，发现了什么根据uncertainly去训练网络模型的论文，给我看的一头雾水，画了一天去恶补贝叶斯神经网络和数学相关的知识。
论文原文为《Autobalanced Multitask Node embedding Framework for intelligent Education》是一个有图网络对教育数据进行Embedding的文章，但是我还没有看完，已经卡在贝叶斯网络、蒙特卡洛评估器这里了，给人烦的，速来补充基础。

联合概率、边缘概率、条件概率、贝叶斯定理

概率论基础知识参考链接[2]，我个人认为知识只是应用层面，不对其数学理论进行深究已经足够。

背景

传统神经网络 传统的神经网络模型整体框架为去寻找w、b矩阵去得到结果predict，然后进行反向传播去得到使得loss最小的w、b矩阵。简化为如下公式，其中Y为label，X为input。即通过input利用w、b得到predict然后计算误差，反向传播，更新w、b。当误差最小的时候的w、b即为所求

贝叶斯神经网络 但是贝叶斯神经网络就不一样了，涉及到概率问题，传统的神经网络什么值都是确定的，无论是参数还是输入还是输出，这么说有点点泛泛，但是任何地方都没有用到概率，而贝叶斯神经网络中使用分布去表示参数的。这就是传统和贝叶斯不一样的地方了。
贝叶斯神经网络优化的目标用到的并不是权重确定的数值，而是一个分布。其有一个假设，就是假设其神经元的权重服从高斯分布。现实生活中存在的情况就是大部分人都是普通人，符合高斯分布的情况。那么神经元的是一个分布得出的了，通过采样得出，那么就没有办法进行反向传播，咦，这个时候，重参数化就提出来了，参考链接[3]。其将权重分布的参数单独提出来，然后进行优化。最后得到的分布即为最好的权重分布，最后使用权重分布去生成w、b然后使用网络模型进行前向传播进行预测即可。
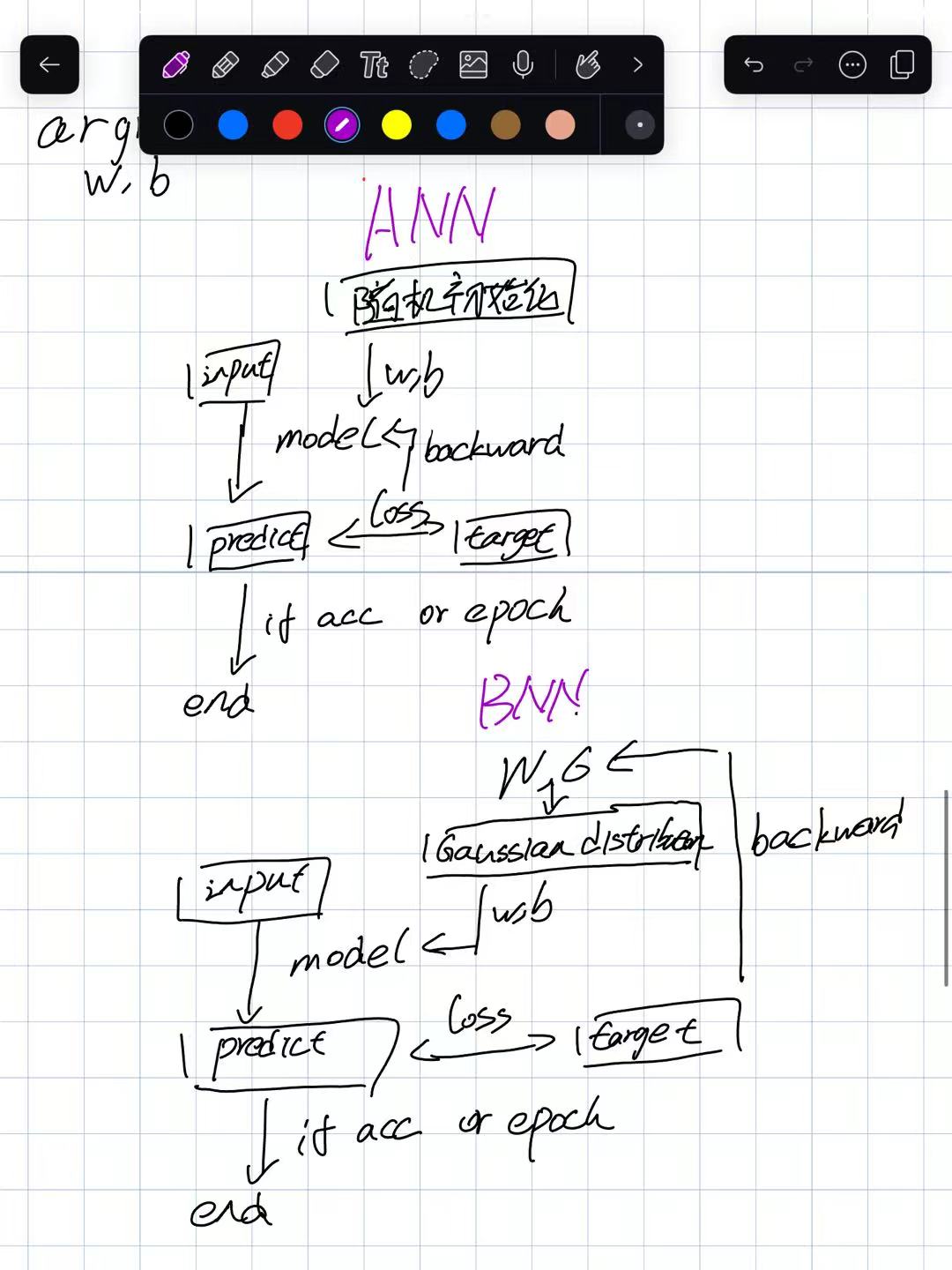
二者流程图如下，通过区别可以发现ANN主要优化的是参数w、b至于BNN（贝叶斯神经网络）则是优化的$\mu$和$\sigma$.然后生成权重在进行model预测，明白了吧。下面说说细节。

条件概率

$p(A|B)$表示在A发生的前提下B发生的概率。
由贝叶斯定理可得
$p(A|B)=P(B/A)P(A)/P(B)$
后验概率可以由先验概率的出。
而在贝斯神经网络中，需要用已知数据集去得到权重，用条件概率的话说，因是我给你数据，果是你得到权重。用数学公式表示为$P(W|D)$$D$为数据集，$W$为权重。
由贝叶斯准则有$p(W|D)=p(D/W)p(W)/p(D)$
$p(D/W)$为前向传播过程得到的预测值概率
$p(W)$为权重的分布概率
$p(D)$为数据集本身的分布概率
$p(D)$为对$P(D,W)$对$W$所有维度进行积分相乘。当维度很多时计算困难。

实际上，我们所要寻找的就是权重的分布，换种思路，从可能的函数集合中寻找一个满足条件的函数，称为“变分”。因为所拟合的分布会存在最值的情况，我觉得是因为用分布去采样生成权重，采样生成的权重数值好歹差不多了，如果分布的概率密度函数有好几个凸点，表示每次采样在好几个凸点周围产生的概率差不多，分布太均匀了，我们需关注的就是唯一一个最高点，作为我们的权重，此时最值是我们需要投入大量关注的点，即其附近值的概率最大，与高斯分布相似**。因此问题转换成，需要寻找一个高斯分布去拟合所要找的分布。**这时候我们引入一个新概念，KL散度,参考链接[3]，其是衡量两个分布是否相似的指标。即$KL(q(W)||p(W|D))$,进行如下公式推导。$q(w)$为我们所要求的高斯分布。去拟合$p(W|D)$,因为$p(W|D)$很难找，所以采用这种变分思想去寻找近似的$p(W|D)$,即$q(w)$。

不想看可以直接看结论。
$KL(q(W)||p(W|D))=logq(W)-logp(W)-logp(D|W)+logP(D)$
KL散度越小表示两个分布越接近。而$logP(D)$只与数据有关，与参数无关，这里我们只考虑前三位，使前三位最小的权重分布即为我们所要的权重分布。此时目标转换成最小化前三函数即可，是我们模型最终的损失函数，

$q(W)$ 为要求解的分布,正态分布。 每一个神经元都有单独的分布
$p(W)$为权重的先验分布，根据所给分布进行计算。
$p(D|W)$为已知w的情况，D的分布。
代码来自链接[1].

import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Normal
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt


class Linear_BBB(nn.Module):
    """
        Layer of our BNN.
    """
    def __init__(self, input_features, output_features, prior_var=1.):
        """
            先验分布是以均值为0，方差为1的高斯分布
            Initialization of our layer : our prior is a normal distribution
            centered in 0 and of variance 1.
        """
        # initialize layers
        super().__init__()
        # set input and output dimensions
        # 输入和输出的维度
        self.input_features = input_features
        self.output_features = output_features

        # initialize mu and rho parameters for the weights of the layer
        # 初始化该层的权重和偏置  ====》y = w * x + b
        # 该层的每一个权重和偏置都有自己的方差和均值
        self.w_mu = nn.Parameter(torch.zeros(output_features, input_features))
        self.w_rho = nn.Parameter(torch.zeros(output_features, input_features))

        # initialize mu and rho parameters for the layer's bias
        # 网络的参数是权重和偏置的期望与方差
        # 实际的参数，即参与计算的参数是从这个分布里面采样的
        self.b_mu = nn.Parameter(torch.zeros(output_features))
        self.b_rho = nn.Parameter(torch.zeros(output_features))

        # initialize weight samples (these will be calculated whenever the layer makes a prediction)
        self.w = None
        self.b = None

        # initialize prior distribution for all of the weights and biases
        # 假设该层的所有权重和偏置均为正态分布
        self.prior = torch.distributions.Normal(0, prior_var)

    def forward(self, input):
        """
          Optimization process
        """
        # sample weights
        """
            从均值为0，方差为1的高斯分布中采样一些样本点 u + log(1 + exp(p)) * w'
            一种重参数技巧，最早用于VAE中
            对于原本服从 N~（u , p）的随机变量w，先不直接根据这个分布采样，而是先根据标准正态分布采样 w_epsilon
            随后根据 w = u + log(1 + exp(p)) * w' 得到实际的采样值，这样做的目的是为了便于反向传播
        """

        w_epsilon = Normal(0, 1).sample(self.w_mu.shape)
        self.w = self.w_mu + torch.log(1 + torch.exp(self.w_rho)) * w_epsilon

        # sample bias
        b_epsilon = Normal(0, 1).sample(self.b_mu.shape)
        self.b = self.b_mu + torch.log(1 + torch.exp(self.b_rho)) * b_epsilon

        # record log prior by evaluating log pdf of prior at sampled weight and bias
        """
            对已经采样的值，计算其在预先定义的分布上的对数形式得到的值（log_prob(value)是计算value在定义的正态分布（mean,1）中对应的概率的对数）
            损失函数是要最大化elbo下界：L = sum[log(q(w))]- sum(log P(w)) - sum(log P(y_i | w, x_i))
        """
        # 计算 p（w）
        w_log_prior = self.prior.log_prob(self.w)
        b_log_prior = self.prior.log_prob(self.b)
        self.log_prior = torch.sum(w_log_prior) + torch.sum(b_log_prior)

        # record log variational posterior by evaluating log pdf of normal distribution defined by parameters with respect at the sampled values
        # 计算 q(w)，也有称其为 p(w|theta)的
        # q(w) 表示根据当前的网络参数 w_mu，w_rho，b_mu，b_rho 计算q（w），也就是说q（w）就是我们损失函数要求解的分布
        self.w_post = Normal(self.w_mu.data, torch.log(1 + torch.exp(self.w_rho)))
        self.b_post = Normal(self.b_mu.data, torch.log(1 + torch.exp(self.b_rho)))
        self.log_post = self.w_post.log_prob(self.w).sum() + self.b_post.log_prob(self.b).sum()

        return F.linear(input, self.w, self.b)


class MLP_BBB(nn.Module):
    def __init__(self, hidden_units, noise_tol=.1,  prior_var=1.):

        # initialize the network like you would with a standard multilayer perceptron, but using the BBB layer
        super().__init__()
        self.hidden = Linear_BBB(1, hidden_units, prior_var=prior_var)
        self.out = Linear_BBB(hidden_units, 1, prior_var=prior_var)
        self.noise_tol = noise_tol # we will use the noise tolerance to calculate our likelihood

    def forward(self, x):
        # again, this is equivalent to a standard multilayer perceptron
        x = torch.sigmoid(self.hidden(x))
        x = self.out(x)
        return x

    def log_prior(self):
        # calculate the log prior over all the layers
        return self.hidden.log_prior + self.out.log_prior

    def log_post(self):
        # calculate the log posterior over all the layers
        return self.hidden.log_post + self.out.log_post

    # 损失函数的计算
    def sample_elbo(self, input, target, samples):
        # we calculate the negative elbo, which will be our loss function
        #initialize tensors
        outputs = torch.zeros(samples, target.shape[0])
        log_priors = torch.zeros(samples)
        log_posts = torch.zeros(samples)
        log_likes = torch.zeros(samples)
        # make predictions and calculate prior, posterior, and likelihood for a given number of samples
        # 蒙特卡洛近似，根据给定的样本数采样
        # 蒙特卡洛在这里用来计算前向传播的次数，所以蒙特卡洛可能与模型权重的不确定性有关
        for i in range(samples):
            outputs[i] = self(input).reshape(-1)  # make predictions
            log_priors[i] = self.log_prior() # get log prior
            log_posts[i] = self.log_post() # get log variational posterior
            log_likes[i] = Normal(outputs[i], self.noise_tol).log_prob(target.reshape(-1)).sum() # calculate the log likelihood
        # calculate monte carlo estimate of prior posterior and likelihood
        log_prior = log_priors.mean()
        log_post = log_posts.mean()
        log_like = log_likes.mean()
        # calculate the negative elbo (which is our loss function)
        loss = log_post - log_prior - log_like
        return loss



def toy_function(x):
    return -x**4 + 3*x**2 + 1

# toy dataset we can start with
x = torch.tensor([-2, -1.8, -1, 1, 1.8, 2]).reshape(-1,1)
y = toy_function(x)

net = MLP_BBB(32, prior_var=10)
optimizer = optim.Adam(net.parameters(), lr=.1)
epochs = 1000
for epoch in range(epochs):  # loop over the dataset multiple times
    optimizer.zero_grad()
    # forward + backward + optimize
    loss = net.sample_elbo(x, y, 1)
    loss.backward()
    optimizer.step()
    if epoch % 10 == 0:
        print('epoch: {}/{}'.format(epoch+1,epochs))
        print('Loss:', loss.item())
print('Finished Training')


# samples is the number of "predictions" we make for 1 x-value.
# 网络训练完成后，对于随机给定的输入值 x，计算模型的输出值 y
# samples 表示采样次数，即预测多少次，最后对这些次的结果取平均值
samples = 10
x_tmp = torch.linspace(-5, 5, 100).reshape(-1, 1)
y_samp = np.zeros((samples, 100))
print(x_tmp.shape)
for s in range(samples):
    y_tmp = net(x_tmp).detach().numpy()
    y_samp[s] = y_tmp.reshape(-1)
plt.plot(x_tmp.numpy(), np.mean(y_samp, axis=0), label='Mean Posterior Predictive')
plt.fill_between(x_tmp.numpy().reshape(-1), np.percentile(y_samp, 2.5, axis=0),
                 np.percentile(y_samp, 97.5, axis=0), alpha=0.25, label='95% Confidence')
plt.legend()
plt.scatter(x, toy_function(x))
plt.title('Posterior Predictive')
plt.show()

if __name__ == '__main__':
    print("done!")