F2. Game on Sum (Hard Version)

F2. Game on Sum (Hard Version)
dp方程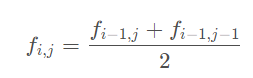： f[i][j]=i(i==j时)
复杂度nm，考虑优化，观察到转移方程和组合数的公式类似

考虑 (i,i)对(n,m)的贡献 即(i,i)到(n,m)路径的数量 往下 n-i次 ，往右下m-i次 (第一次只能往下) 所以路径数为C(n-i-1,m-i) 再处理权值 初始值为i，每次向下要除以2

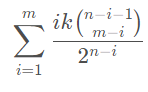
//#pragma GCC optimize(2)
//#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
#define pb push_back
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int inf=8e18;
const int maxn=1e6+100;
const int mod=1e9+7;
int n,m,k;
int fac[maxn],inv[maxn];
int dp[maxn];
void init()
{
	fac[0]=fac[1]=1;
	inv[0]=inv[1]=1;
	for(int i=2;i<maxn;i++)
	{
		fac[i]=fac[i-1]*i%mod;
		inv[i]=(mod-mod/i)%mod*inv[mod%i]%mod;
	}
	for(int i=1;i<maxn;i++)
	{
		inv[i]=inv[i-1]*inv[i]%mod;
	}
}
int C(int a,int b)
{
	if(a<b||a<0||b<0)return 0;
	return fac[a]*inv[b]%mod*inv[a-b]%mod;
}
int qpow(int a,int b)
{
	int ans=1;
	while(b)
	{
		if(b&1)ans=ans*a%mod;
		a=a*a%mod;
		b=b>>1;
	}
	return ans%mod;
}
signed main()
{
	init();
	int tt;
	cin>>tt;
	while(tt--)
	{
		cin>>n>>m>>k;
		if(n==m)
		{
			cout<<m*k%mod<<"\n";
			continue;
		}
		int ans=0;
		for(int i=1;i<=m;i++)
		{
			ans=(ans+i*C(n-i-1,m-i)%mod*qpow(qpow(2,n-i),mod-2)%mod)%mod;
		}
		ans=((ans+mod)*k)%mod;
		cout<<ans<<"\n";
	}
}