数学知识：高斯消元

---

前言

复习acwing算法基础课的内容，本篇为讲解数学知识：高斯消元，关于时间复杂度：目前博主不太会计算，先鸽了，日后一定补上。

---

一、高斯消元

高斯消元运用于去解多元函数的解，如下图所示：

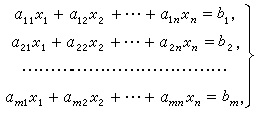
利用高斯消元，我们可以在很短的时间内去判断这个多元方程是否有解，如果是由唯一组解的情况下可以解出这一解，高斯消元的计算过程类似于线性代数，如何去解这个问题，我们在下文会根据题目进行一些规定和分析.

---

二、例题，代码

AcWing 883. 高斯消元解线性方程组

本题链接：AcWing 883. 高斯消元解线性方程组
本博客提供本题截图：

本题解析

首先来说明以下本题的几个需要声明的量和值，然后再介绍高斯消元：
我们用二维数组a去存储整个方程组，注意我们在做除法的时候因为我们表达一个分数比较复杂，所以这里用的是小数，用小数就有了精度缺失这个问题，比如1 / 3 * 3这个结果应该是等于1的，但是我们表示成小数之后运算结果为0.999...，故我们在表达0这个量的时候，因为精度问题，我们可以用一个特别小的数去当0，当运算结果小于我们设定的这个十分小的数的时候，我们就默认为0，在本题中，我们用const double eps = 1e-6;去表达这个无穷小的数.本题中，我们用c去表示列，用r去表示行

我们在解的过程中，规定如下解法：
把整个多元函数集化简成如下图所示的情况：（空白部分均为0）

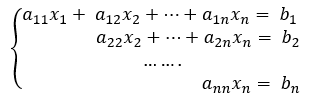
如果最后的化简结果如上图所示，那么就有唯一的一组解；
如果最后化简得到的式子中有0 = 非零这种特殊情况的，没有解；
如果最后化简得到的式子中有0 = 0这种情况的，有无数组解.

下面来规定几个高斯消元的操作（线代中的计算方法）
把某一行乘一个非零的数
交换某两行
将某行的若干倍加到另一行上

下面来正式介绍高斯消元在代码上如何实现求解的各种操作：
高斯消元分以下几个步骤：
枚举每一列c：
1.找到绝对值最大的一行

for (c = 0, r = 0; c < n; c ++ )
{
	int t = r;
	for (int i = r; i < n; i ++ )
		if (fabs(a[i][c]) > fabs(a[t][c]))
			t = i;

	if (fabs(a[t][c]) < eps) continue;//如果最大的一行都已经是0了，那么就没必要操作这一列了，直接continue即可
}

2.将该行换到最上面

for (int i = c; i < n + 1; i ++ ) swap(a[t][i], a[r][i]);

3.将该行第一个数变成1
这步的操作其实就是让该行的每一列元素都除以第一个不为0的列的值，这里需要注意必须倒着进行，否则如果第一个数除以本身的话，后面的数处理起来就比较麻烦了，解决方法可以是存储一下第一个数，但是没有这个必要，倒着进行for循环即可解决这个问题

for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];

4.将下面所有行的第c列消成0
这里注意我们已经让第r行，第c列的数变成1了，所以我们在消后面几行的时候，只需要让第i行第j列的元素减去该行第c列元素的值乘第r行j列元素的值

for (int i = r + 1; i < n; i ++ )
	if (fabs(a[i][c]) > eps)       //这个数不是0再进行操作
		for (int j = n; j >= c; j -- )
			a[i][j] -= a[r][j] * a[i][c];

下面来说说求解的过程：
按照常理来说，我们应该枚举到最后，我们的行数r应该是枚举到最后一行了，如果没有，证明这里有特殊情况出现了：即没有解或者有无穷多组解，下面我们来讨论这种情况：

if (r < n)
{
	for (int i = r; i < n; i ++ )
		if (fabs(a[i][n]) > eps)    //即等式左边全部为0，但是等式右边的值不为0
			return 2;               //证明无解
	return 1;                       //证明有无穷多组解
}

接下来看一下有解的代码，并计算解：
从下往上进行代值，得到方程的解，这里建议自己动手模拟一下这个过程

for (int i = n - 1; i >= 0; i -- )
	for (int j = i + 1; j < n; j ++ )
		a[i][n] -= a[j][n] * a[i][j];

	return 0;                        //证明有解

AC代码

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 110;
const double eps = 1e-6;

int n;
double a[N][N];


int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i < n + 1; i ++ ) swap(a[t][i], a[r][i]);
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];

        for (int i = r + 1; i < n; i ++ )
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2;
        return 1;
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[j][n] * a[i][j];

    return 0;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            cin >> a[i][j];

    int t = gauss();

    if (t == 0)
    {
        for (int i = 0; i < n; i ++ ) printf("%.2lf\n", a[i][n]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");

    return 0;
}

AcWing 884. 高斯消元解异或线性方程组

本题链接：AcWing 884. 高斯消元解异或线性方程组
本博客提供本题截图：

本题解析

本题思路和上题思路基本一致，注意4.将下面所有行的第c列消成0 这一步，其实就和和第r行的每一列的对应元素进行异或运算
异或运算中满足a ^ b = c, c ^ b = a，故我们在求解每个元素的值得时候可以利用异或去运算求解.

AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n;
int a[N][N];

int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )
            if (a[i][c])
                t = i;

        if (!a[t][c]) continue;

        for (int i = c; i <= n; i ++ ) swap(a[r][i], a[t][i]);
        for (int i = r + 1; i < n; i ++ )
            if (a[i][c])
                for (int j = n; j >= c; j -- )
                    a[i][j] ^= a[r][j];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (a[i][n])
                return 2;
        return 1;
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            if (a[i][j])
                a[i][n] ^= a[j][n];

    return 0;
}

int main()
{
    cin >> n;

    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            cin >> a[i][j];

    int t = gauss();

    if (t == 0)
    {
        for (int i = 0; i < n; i ++ ) cout << a[i][n] << endl;
    }
    else if (t == 1) puts("Multiple sets of solutions");
    else puts("No solution");

    return 0;
}

---

三、时间复杂度

关于高斯消元各步操作的时间复杂度以及证明，后续会给出详细的说明以及证明过程，目前先鸽了。