关于最速下降法与固定步长梯度法的研究

努力上进的math boy

已于 2024-05-02 00:20:48 修改

阅读量750

点赞数 26

分类专栏：运筹学文章标签：算法 matlab

于 2024-05-01 19:24:31 首次发布

本文链接：https://blog.csdn.net/qq_52176723/article/details/138368245

版权

运筹学专栏收录该内容

3 篇文章 0 订阅

订阅专栏

1.引言

梯度下降法（Gradient Descent）是一种实现简单，且大部分情况下都能够很好地运行的一种优化算法，是为了极小化函数而设计的方法，仅使用目标函数的梯度作为信息进行优化，梯度下降法在各个领域广泛应用，尤其是人工智能深度学习方面。受到梯度方向为函数值增加最快的方向的启发，每次搜索方法为梯度方向的负方向，再选择合适的步长，即可使函数值减少。

下面给出梯度是函数值增加最快的方向证明，记函数 $f$ 在 $x$ 处， $\vec{d}$ 方向的增长率为 $\langle{\vec{d},\nabla{f(x)}}\rangle$ ， $||\vec{d}||=1$ ,使用柯西-施瓦茨不等式：

$\langle{\vec{d},\nabla{f(x)}}\rangle\ \ \leq \ \ ||\nabla{f(x)})||$

若令 $\vec{d}=\nabla{f(x)}/||\nabla{f(x)}||$ ，则有

$\langle{\vec{d},\nabla{f(x)}}\rangle=||\nabla{f(x)})||$

因此，梯度方向 $\nabla{f(x)}$ 就是函数 $f$ 在 $x$ 处增加最快的方向，而梯度负方向 $-\nabla{f(x)}$ 就是函数减少最快的方向。以 $x^{(0)}$ 作为初始搜索点，沿着 $-\nabla{f(x)}$ 方向进行搜索，由泰勒展开可得：

$f(x^{(0)}-\alpha\nabla{f(x^{(0)})})=f(x^{(0)})-\alpha||\nabla{f(x^{(0)})}||^{2}+o(\alpha)$

因此，如果 $\nabla{f(x^{0})}\neq 0$ ，当 $\alpha> 0$ 充分小的时候，有

$f(x^{(0)}-\alpha\nabla{f(x^{(0)})})<f(x^{(0)})$

。从目标函数极小化的角度看，新得到的点相比于 $x^{(0)}$ 有所改善，这就是梯度下降法思路的理论支撑。下面介绍两种梯度下降法的具体实现，在下一章，还会介绍基于共轭方向法（Conjugate Direction Method）的另一种优化思路，并给出结合了梯度下降和共轭方向法的著名方法共轭梯度法（Conjugate Gradient Method），该方法是在工程领域应用广泛的一种优化方法，是真正具有实用性的方法。

2.最速下降法

最速下降法（Steepest Descent）是梯度下降法的一种具体实现，其理念为在每次迭代中，以梯度的负方向作为下降方向，寻找一个合适的步长 $\alpha_{k}$ ，使得目标函数 $f$ 能够得到最大程度的减小。 $\alpha_{k}$ 可以视为是一维搜索函数的极小值点，即：

$\varphi _{k}(\alpha)=arg\ minf(x^{(k)}-\alpha\nabla{f(x^{(k)})})$

2.1最速下降法实现步骤

最速下降法的实现步骤可以归纳如下：

1. 给定 $x_{0}\in{R^{n}},0\leq \varepsilon\ll 1,k=0;$

2. 计算 $d_k=-g_k;$ 如果 $||g_k||\leq \varepsilon$ ，停止搜索；

3. 求步长 $\alpha$ ，使得 $f(x_k+\alpha_kd_k)=min\ f(x_k+\alpha{}d_k)$ ；

4. 计算 $x_{k+1}=x_k+\alpha_kd_k$ ；

5. k=k+1，转2.

2.2最速下降法代码实现

function [x,y] = sd(f,g,x0,tolerance)
n=length(x0);   %确定变量x0的维数
k=1;    %用于计数
x=zeros(n,1);   %设计x矩阵储存每次迭代的x近似值
d=zeros(n,1);   %设计d矩阵储存每次迭代的梯度值
x(:,k)=x0;
d(:,k)=-g(x(:,k));
y(k)=f(x(:,k));
while norm(d(:,k))>=tolerance  %当梯度范数不小于给定容忍值时，进入循环
    alpha1=2;
    alpha2=1;
    dphi1=g(x(:,k)+alpha1*d(:,k))'*d(:,k);
    dphi2=g(x(:,k)+alpha2*d(:,k))'*d(:,k);
    while abs(dphi2)>=0.0001  %割线法求极小化alpha的函数
        if abs(dphi2-dphi1)~=0
            t=alpha2-dphi2*(alpha2-alpha1)/(dphi2-dphi1);
            alpha1=alpha2;
            alpha2=t;
            dphi1=g(x(:,k)+alpha1*d(:,k))'*d(:,k);
            dphi2=g(x(:,k)+alpha2*d(:,k))'*d(:,k);
        end
    end
    alpha=alpha2;    %经过割线法优化后的alpha2即是所求的alpha值
    x(:,k+1)=x(:,k)+alpha*d(:,k); %更新新的迭代点x
    d(:,k+1)=-g(x(:,k+1));  %更新梯度信息
    y(k+1)=f(x(:,k+1));   %更新新的函数值信息
    k=k+1;
end
semilogy((1:k),y,'r*')
xlabel '迭代次数'
ylabel '优化值'
title '最速下降法随迭代次数，函数值变化情况'
end

以上代码是最速下降法的一般表达，但要注意容忍值tolerance一般不要设置太小，因为太小的容忍值往往达不到，一般设置 $10^{-3}\sim 10^{-5}$ 为宜，一维搜索停机准则亦同理。

2.3性能测试

使用函数

$f(x_1,x_2,x_3)=(x_1-4)^4+(x_2-3)^2+4(x_3+5)^4$

作为测试函数，初始搜索点为

$x^{(0)}=\begin{bmatrix} 4\\ 2\\ -1 \end{bmatrix}$

在Matlab中输入如图1

图1

近似值 $x$ 搜索结果如图2

图2

函数值 $y$ 的优化效果如图3

图3

因为此函数是二次型函数，当 $\alpha_k=\frac{g^{(k)^T}g^{k}}{g^{(k^T)}Qg^{(k)}}$ 时，有

$\varphi _{k}(\alpha)=arg\ minf(x^{(k)}-\alpha\nabla{f(x^{(k)})})$

成立，只需3步即可找到函数极小值点，但此方法只适用于二次型函数，为了适应大多数函数，代码没有照此写，而是按照一维搜索求极小点的方法运行。

2.4最速下降法的改进(BB步)

Barzilai-Borwein提出两点步长梯度法，其基本思想是利用迭代当前点以及前一点的信息来确定步长因子，按袁亚湘老师的说法就是当前步的步长用上一步的最优步长，效果反而很好，即 $\alpha_k=\alpha_{k-1}$ 。这里不再讨论其收敛性，仅给出相应代码和效果对比。

function [x,y] = bbgd(f,g,x0,tolerance)
n=length(x0);
k=1;
x=zeros(n,1);
d=x;
x(:,k)=x0;
d(:,k)=-g(x(:,k));
y(k)=f(x(:,k));
while norm(d(:,k))>tolerance
    alpha1=10;
    alpha2=9;
    dphi1=g(x(:,k)+alpha1*d(:,k))'*d(:,k);
    dphi2=g(x(:,k)+alpha2*d(:,k))'*d(:,k);
    if k==1
        while abs(dphi2)>0.0001
              if abs(dphi2-dphi1)
                 t=alpha2-dphi2*(alpha2-alpha1)/(dphi2-dphi1);
                 alpha1=alpha2;
                 alpha2=t;
                 dphi1=g(x(:,k)+alpha1*d(:,k))'*d(:,k);
                 dphi2=g(x(:,k)+alpha2*d(:,k))'*d(:,k);
              else 
                  return
              end
        end
        alpha(k)=alpha2;
        x(:,k+1)=x(:,k)+alpha(k)*d(:,k);
        d(:,k+1)=-g(x(:,k+1));
        y(k+1)=f(x(:,k+1));
        k=k+1;
    else
        while abs(dphi2)>0.0001
            if abs(dphi2-dphi1)
                t=alpha2-dphi2*(alpha2-alpha1)/(dphi2-dphi1);
                alpha1=alpha2;
                alpha2=t;
                dphi1=g(x(:,k)+alpha1*d(:,k))'*d(:,k);
                dphi2=g(x(:,k)+alpha2*d(:,k))'*d(:,k);
            else
                return
            end
        end
        alpha(k)=alpha2;
        x(:,k+1)=x(:,k)+alpha(k-1)*d(:,k);
        d(:,k+1)=-g(x(:,k+1));
        y(k+1)=f(x(:,k+1));
        k=k+1;
    end
end
semilogy((1:k),y,'r*')
xlabel '迭代次数'
ylabel '优化值'
title 'BB步下降法随迭代次数，函数值变化情况'
end

测试函数为

$f(x_1,x_2)=100x_{1}^{2}+x_{2}^{2}$

该函数条件数很差，用最速下降法会产生锯齿效应，两步之间的函数值几乎不下降，效果如图

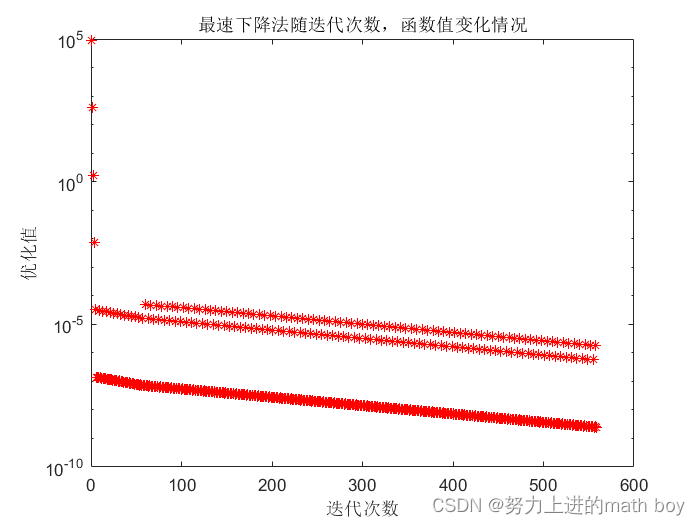
图4

而BB步在这种条件数下，收敛速度却很快，如图

图5

3.步长固定梯度法

步长固定梯度法（Fixed Step Gradient Method）是另外一种梯度法的具体实现，在选择方向时与最速下降法已知，但省去了极小化步长 $\alpha$ 的步骤，而是采用固定步长，这使得设计更为简单，计算复杂度更低。

3.1步长固定梯度法实现步骤

1. 给定 $x_{0}\in{R^{n}},0\leq \varepsilon\ll 1,k=0$ 和步长 $\alpha$ ；

2. 计算 $d_k=-g_k;$ 如果 $||g_k||\leq \varepsilon$ ，停止搜索；

4. 计算 $x_{k+1}=x_k+\alpha{}d_k$ d；

5. k=k+1，转2.

3.2步长固定梯度法代码实现

function [x_last,y_last] = fsgd(f,g,x0,tolerance,alpha)  %与最速下降法不同的是，该方法的alpha为固定步长
n=length(x0);   %确定变量x0的维数
k=1;    %用于计数
x=zeros(n,1);   %设计x矩阵储存每次迭代的x近似值
d=zeros(n,1);   %设计d矩阵储存每次迭代的梯度值
x(:,k)=x0;
d(:,k)=-g(x(:,k));
y(k)=f(x(:,k));
while norm(d(:,k))>=tolerance  %当梯度范数不小于给定容忍值时，进入循环
    x(:,k+1)=x(:,k)+alpha*d(:,k); %更新新的迭代点x
    d(:,k+1)=-g(x(:,k+1));  %更新梯度信息
    y(k+1)=f(x(:,k+1));   %更新新的函数值信息
    k=k+1;
end
x_last=x(:,end);
semilogy((1:k),y,'r*')
xlabel '迭代次数'
ylabel '优化值'
title '步长固定梯度法随迭代次数，函数值变化情况'
y_last=y(:,end);
end

3.3性能测试

同最速下降法一样的测试函数,结果如图6

图6

可视化结果如图7

图7

可以看到，步长固定梯度法迭代次数远超过最速下降法，并且 $\alpha$ 的值需要手工设置，只有设置到一定范围内，该方法才会收敛，在下文4部分会给到 $\alpha$ 具体的收敛范围。

4.梯度方法收敛定理

此处笔者证明思路采用Edwin.K.P.Chong与Stanislaw H.Zak著,孙志强译的《最优化导论（第四版）》，另外的证明思路可以参考袁亚湘老师著的《最优化理论与方法》，此书中利用康托洛维奇不等式证明了最速下降法全局收敛性，读者可自行查看书籍对照。首先给定二次型目标函数 $f$ ，将函数进行变形，便于讨论。即设函数 $V(x)$ 如下：

$V(x)=f(x)+\frac{1}{2}x^{*^{T}}Qx=\frac{1}{2}(x-x^*)^{T}Q(x-x^*)$

其中 $x^*$ 为函数 $f$ 的极小值点，因此 $V(x)$ 相对于 $f$ 仅相差一个常数，不影响极小值点位置，以此再给出引理2.1

引理4.1

迭代公式 $x^{(k+1)}=x^{(k)}-\alpha_kg^{(k)}$

满足 $V(x^{(k+1)})=(1-\gamma _k)V(x^{(k)})$

其中， $g^{(k)}=Qx-b$ 。如果 $g^{(k)}=0,\gamma _k=1$ ；如果 $g^{(k)}\neq 0$

$\gamma _k=\alpha_k\frac{g^{(k)^T}Qg^{(k)}}{g^{(k)^T}Q^{-1}g^{(k)}}(2\frac{g^{(k)^T}g^{(k)}}{g^{(k)^T}Qg^{(k)}}-\alpha_k)$

证明手稿如图8

图8

由于 $\gamma _k=1-\frac{V(x^{(k+1)})}{V(x^{k})}$ ，因此对于所有的 $k$ ，都有 $\gamma _k\leq 1$ 。如果 $\gamma _k=1$ ，那么 $V(x^{(k+1)})=0$ ，此时 $x^{(k+1)}=x^*$ ，即达到极小值点。这说明当且仅当 $g^{(k)}=0$ 或 $g^{(k)}$ 是矩阵 $Q$ 的特征向量（后续会给出证明，此处不证）时， $\gamma _k=1$ 。

定理4.1

$\{x^{(k)}\}$ 表示梯度方法产生的迭代点序列， $x^{(k+1)}=x^{(k)}-\alpha_kg^{(k)}$ 。 $\gamma _k$ 按照引理8.1中的方式定义，且假定对于所有 $k$ ，都有 $\gamma _k>0$ 。那么，当且仅当

$\sum_{k=0}^{\infty}\gamma _k=\infty$

时， $\{x^{(k)}\}$ 在任何初始值 $x^{(0)}$ 下都收敛到极小值点 $x^*$ 。

定理4.1证明如图9

图9

定理4.1适用于所有以梯度下降方法产生的点列收敛判断，在随后的固定梯度下降法中的收敛性判定也是通过该定理来证明的。需要注意的是，定理中 $\gamma_k>0$ 的假设十分重要，没有该假设定理4.1不成立。

在证明最速下降法收敛定理前引入瑞利不等式，对任意的 $Q=Q^{\text{T}}>0$ ，有

$\lambda _{min}(Q)||x||^{2}\leq x^{T}Qx\leq\lambda_max(Q)||x||^2$

其中 $\lambda_{min}(Q)$ 表示矩阵 $Q$ 的最小特征值， $\lambda_{max}(Q)$ 为矩阵 $Q$ 的最大特征值。当 $Q=Q^{\text{T}}>0$ 时，有

$\lambda_{min}(Q^{-1})=\frac{1}{\lambda_{max}(Q)}$

$\lambda_{max}(Q^{-1})=\frac{1}{\lambda_{min}(Q)}$

$\lambda _{min}(Q^{-1})||x||^{2}\leq x^{T}Q^{-1}x\leq\lambda_max(Q^{-1})||x||^2$

此时结合瑞利不等式，可以给出最速下降法的收敛定理。

最速下降法(SD)收敛定理

图10

由定理4.1可知，此时 $x^{(k)}\rightarrow x^*$ ，最速下降法收敛。

再考虑固定步长的梯度下降法收敛性，因为该方法收敛性证明与最速下降法方法相同，故一同证明。在该方法中，对于所有 $k$ ，步长 $\alpha_k=\alpha\in{R}$ ，迭代公式为

$x^{(k+1)}=x^{k}-\alpha{}g^{(k)}$

固定步长的梯度法简单实用。由于步长固定，在每步迭代中，不需要开展一维搜索确定步长 $\alpha_k$ 。但该方法的步长 $\alpha$ 也不是可以任意选取的，下面定理给出了固定步长的梯度下降法要收敛时， $\alpha$ 必须要满足的充要条件。

步长固定下降法收敛定理

对于步长固定梯度法，当且仅当步长

$0<\alpha<\frac{2}{\lambda_{max}(Q)}$

时， $x^{(k)}\rightarrow x^*$ 。

证明如图9

图11

5.梯度方法收敛率

条件数定义

定义

$r=cond(Q)=\frac{\lambda_{max}(Q)}{\lambda_{min}(Q)}=||Q||||Q^{-1}||$

收敛阶数定义

存在一个序列 $\{x^{(k)}\}$ ，能够收敛到 $x^*$ ，即 $\lim_{k\rightarrow \infty}||x^{(k)}-x^*||=0$ 。如果

$0<\lim_{k\rightarrow \infty}\frac{||x^{(k+1)}-x^*||}{||x^{(k)}-x^*||}<\infty$

则序列 $\{x^{(k)}\}$ 的收敛阶数为 $p$ ，其中 $p\in{R}$ 。

序列收敛阶数是评价收敛方法快慢的指标，阶数越高，收敛速度越快，有时候也把阶数直接称为收敛率。

最速下降法的收敛率

利用最速下降法求解二次型函数的极小点，在任意第k次迭代，都有

$V(x^{(k+1)})\leq \frac{\lambda_{max}(Q)-\lambda_{min}(Q)}{\lambda_{max}(Q)}V(x^{(k)})$

证明如下：

在最速下降法收敛定理证明中，已经证明 $\gamma_k\geq \frac{\lambda_{min}(Q)}{\lambda_{max}(Q)}$ ，因此

$\frac{V(x^{(k)})-V(x^{(k+1)})}{V(x^{(k)})}=\gamma_k\geq \frac{\lambda_{min}(Q)}{\lambda_{max}(Q)}$

整理后可得

$V(x^{(k+1)})\leq \frac{\lambda_{max}(Q)-\lambda_{min}(Q)}{\lambda_{max}(Q)}V(x^{(k)})$

从上式可知，最速下降法至少是线性收敛的。并且当条件数很差的时候，即 $\lambda_{max}\gg \lambda_{min}$ ，此时 $V(x^{(k+1)})\approx V(x^{(k)})$ ，最速下降法几乎不下降，从而收敛速度极慢。

6.总结

最速下降法与步长固定梯度下降法均为梯度下降法的具体实现，但二者的缺点很多。对最速下降法来说，它只关注眼前梯度信息，这与贪心算法思想类似，这使得它在条件数很差的情况下会出现锯齿效应，收敛速度很慢。而步长固定梯度下降法缺点更明显，它需要手动设置一个步长 $\alpha$ ， $\alpha$ 需要试验多次才能确定，并且收敛速度远远低于最速下降法，属于更差的一种优化方法。总而言之，二者都不具有实际应用的能力，需要做一些改进，或是找其他梯度下降法的具体实现来代替，下一章将叙述共轭方向法，共轭方向法是另一种极端，它在出发搜索之前就规划好所有搜索方向，而不管中途的任何信息，但由共轭方向法和最速下降法结合的共轭梯度法是非常不错的方法，许多工程优化问题都会基于共轭梯度法，下一章将作具体阐述。