[数值方法]线性方程组Ax=b的高斯消元法与三角分解法原理和代码实现-MatLab

努力上进的math boy

已于 2024-04-07 14:24:13 修改

阅读量2.1k

点赞数 48

分类专栏：数值方法文章标签： matlab 算法矩阵线性代数

于 2024-04-03 12:44:00 首次发布

本文链接：https://blog.csdn.net/qq_52176723/article/details/137283794

版权

数值方法专栏收录该内容

1 篇文章 0 订阅

订阅专栏

线性方程组求解实际意义：

线性方程组Ax=b的数值求解在实际生活中有重要意义，许多实际问题可归结为线性(代数)方程组机械设备、土建结构的受力分析;经济计划企业管理输电网络、管道系统的参数计算;大型的方程组需要有效的数值解法。本文就来简易介绍一下线性方程组常用的数值解法。

一、上三角线性方程组：

1.上三角线性方程组一般形式：

$\left\{ \begin{array}{l} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n \quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= b_1 \\ \quad \quad \quad \quad \quad \quad \vdots \\ a_{n-2,n-2}x_{n-2} + a_{n-2,n-1}x_{n-1} + a_{n-2,n}x_n = b_{n-2} \\ a_{n-1,n-1}x_{n-1} + a_{n-1,n}x_n \quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= b_{n-1} \\ a_{nn}x_n \quad\quad\quad\quad\quad\quad\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = b_n \end{array} \right.$

提取该方程的系数矩阵，可以得到一个上三角矩阵 $A$ ：

$\left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1,n-1} & a_{1n} \\ & a_{22} & \cdots & a_{2,n-1} & a_{2n} \\ & & \ddots & \vdots & \vdots \\ & & & a_{n-1,n-1} & a_{n-1,n} \\ & & & & a_{nn} \\ \end{matrix} \right]$

对于这样一个方程的解法，我们通常采用回代法来解决。值得注意的是，回代法的思路是解决一般线性方程组的前提，笔者接下来要介绍的高斯消元法和PLU分解法最后求解都要回归到求解上下三角形线性方程组的问题。在这里我们假设该矩阵是非奇异矩阵，因此对角线元素不等于零。

2.回代法的计算方法：

$x_n=b_n/a_{nn}$

$x_k=(b_k-\sum_{i=k+1}^{n}a_{ki}x_i)/a_{kk}$

3.回代法代码实现部分：

function x=rebackword(A,b)
n=size(A,2);
x=zeros(n,1);
for k=n:-1:1
    if k==n
        x(n)=b(n)/A(n,n);
    else
        sum=0;
        for i=k+1:n
            sum=sum+A(k,i)*x(i);
        end
        x(k)=(b(k)-sum)/A(k,k);
    end
end
end

回代法的计算复杂度为 $O(n^2)$

二、下三角线性方程组：

1.下三角线性方程组的一般形式：

$\left\{ \begin{array}{l} a_{11}x_1 \quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= b_1 \\ a_{21}x_1 + a_{22}x_2 \quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= b_2 \\ \quad \vdots \\ a_{n-1,1}x_1 + a_{n-1,2}x_2 + \dots + a_{n-1,n-1}x_{n-1} \quad = b_{n-1} \\ a_{n1}x_1 + a_{n2}x_2 + \dots + a_{n,n-1}x_{n-1} + a_{nn}x_n \;\;= b_n \end{array} \right.$

同样提取该线性方程组的系数矩阵，记为 $A$ ：

$\left[ \begin{array}{cccc} a_{11} & & & \\ a_{21} & a_{22} & & \\ \vdots & \vdots & \ddots & \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{array} \right]$

对于该方程，我们使用前向替换法来解方程组，该过程实际上是回代法的反用

2.前向替换法的计算方法：

$x_1=b_1/a_{11}$

$x_k=(b_k-\sum_{i=1}^{k-1}a_{ki}x_i)/a_{kk}$

3.前向替换法的代码实现：

function x=F_S(A,b)
n=size(A,2);
x=zeros(n,1);
for k=1:n
    if k==1
        x(1)=b(1)/A(1,1);
    else
        sum=0;
        for i=1:k-1
            sum=sum+A(k,i)*x(i);
        end
        x(k)=(b(k)-sum)/A(k,k);
    end
end
end

前向替换法的计算复杂度与回代法相同，为 $O(n^2)$

三、一般线性方程组：

1.高斯消元法：

给定一个一般的线性方程组：

$\left\{ \begin{aligned} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= b_2 \\ &\vdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n &= b_n \end{aligned} \right.$

我们要求解此线性方程组，可以考虑将其化为我们所熟悉的上三角矩阵，再用回代法求出解向量。先提取系数矩阵 $A$ ：

$\left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right]$

再写出其增广矩阵 $\bar{A}$ ：

$\left[ \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} & b_n \\ \end{array} \right]$

1.1.高斯消去法流程解释

对该增广矩阵做初等行变换，因为A为非奇异矩阵，最终可以化为上三角的形式，再用回代法求解。即对Ax=b的一般线性方程组，总是可以通过初等行变换变为Ux=y的形式，其中U为上三角矩阵。转化流程如下：

for r=p+1:n
    m(r,p)=Abar(r,p)/Abar(p,p);
    Abar(r,p)=0;
    for c=p+1:n+1
        Abar(r,c)=Abar(r,c)-mr*Abar(p,c);
    end
end

对该代码流程的解释是：当进行到第p列时，用 $\bar{A}$ 中的r行c列的元素减去p行c列元素乘以系数mr，同时将 $\bar{A}$ r行p列元素变为零（因为该操作就是为了将r行p列元素变为零，所以用r行减去p行的mr倍）。经过有限步后，可以将其化为上三角矩阵。需要注意的是，当 $\bar{A}$ 的p行p列元素为零时，需要交换p行后的一个行k，使得k行p列元素非零。

1.2.选主元策略：

为什么要选主元：

避免对角线元素出现0的情况，导致不能通过乘以某一系数mr来消去对角线下方的元素。

误差传播方面，在使用高斯消元法时，总共需要 $(4N^3+9N^2-7N)/6$ 次算术操作，当N=20时，总的算术操作次数为5910，因为计算机是按固定精度运算，这样计算过程中的误差传播将导致错误的结果。这时，偏序选主元策略、按比例偏序选主元策略或者平衡策略可以用来减少误差。下面来简单介绍一下偏序选主元策略和按比例偏序选主元策略，平衡策略在本文不详细展开，读者可自行查找。

1.2.1.偏序选主元策略

该选主元策略的目的在于将元素中的最大绝对值移到主对角线上，然后用该元素消去列中的元素，因为在进行初等行变换的时候，除数较大不容易出现计算误差，所以这样操作会减少误差传播。在高斯消元法前，应该检查位于主对角线和主对角线下方第p列的所有元素，确定行k，它的元素绝对值在所检查的列中最大，即：

$|a_{kp}|=max\{|a_{pp}|,|a_{p+1p}|,...,|a_{N-1p}|,|a_{Np}|\}$

如果k>p，则交换第k行和第p行，这样每个倍数 $m_{rp}$ 的绝对值都小于1，这样就保证变换后的矩阵U与原矩阵A的对应元素的相对大小一致，导致更小的误差传播。

以下是偏序选主元策略的高斯消去法的代码实现：

偏序选主元策略代码实现：

function [X]=G_R(A,b,n)    %输入：系数矩阵A，常数矩阵b，n为系数矩阵A的阶数
AM=[A b];
for c=1:n
    if max(AM(c:n,c))==0    %如果某一列所有元素都为零，为奇异矩阵，不可求逆，无解
        disp('该矩阵是奇异矩阵');
        return
    end
    k=find(abs(AM(c:n,c))==max(abs(AM(c:n,c)))); %找到c列中最大的元素的位置，记为k
    k=k+c-1;    %修正k的值，因为每次寻找只从c+1行开始寻找，找到的位置应该加c-1
    if k~=c     %如果k与c的值不相等，即矩阵c行不是最大值所在的行，则交换两行位置
        t=AM(c,:);
        AM(c,:)=AM(k,:);
        AM(k,:)=t;
    end
    for r=c+1:n    %消除c+1行以下的元素为零
        mr=AM(r,c)/AM(c,c);
        AM(r,c)=0;
        for cc=c+1:n+1  
            AM(r,cc)=AM(r,cc)-mr*AM(c,cc);  %运行到第r行时，将r行从c+1列开始的所有元素与第c行的c+1列元素乘以相应系数mr相减
        end
    end
end
U=AM(1:n,1:n);  %将AM的n行n列内的所有元素记为U
Y=AM(:,n+1);    %将AM的所有行n+1列的所有元素记为Y
X=zeros(n,1);   %将解向量全部元素赋值0，则AX=b等价于UX=Y
for r=n:-1:1    %利用回代法计算解向量X的每一个值
    if r==n
        X(r,1)=Y(r,1)/U(r,r);   %计算第解向量X的n行1列处的值
    else
        sum=0;
        for rr=r+1:n
            sum=sum+U(r,rr)*X(rr,1);    %计算rr行到n行的解向量乘以r行rr列处对应系数
        end
        X(r)=(Y(r)-sum)/U(r,r);     %计算解向量X中r行处的值
    end
end
end

测试效果

测试系数矩阵A：

$\begin{pmatrix} 4& 8 & 4 &0 \\ 1& 5 & 4 &-3 \\ 1& 4 & 7 & 2\\ 1& 3 & 0 & -2 \end{pmatrix}$

测试常数项矩阵b：

$\begin{pmatrix} 8\\ -4\\ 10\\ -4 \end{pmatrix}$

测试结果：

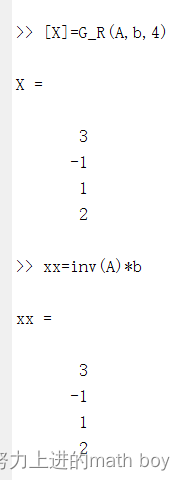
1.2.2.按比例偏序选主元策略

该策略能够在计算中得出更小的误差，首先搜索位于主对角线和主对角线下方第p列的元素，其次元素满足在所在行中其绝对值相对最大。首先搜索第p行到第N行中绝对值最大的元素，称为 $s_{r}$ :

$s_{r}=max\{|a_{rp}|,|a_{rp+1}|,...,|a_{rN}|\},\;\;\;\;r=p,p+1,...,N$

再通过求下式确定第k行：

$\frac{|a_{kp}|}{sk}=max\{\frac{|a_{pp}|}{s_{p}},\frac{|a_{p+1}|}{s_{p+1}},...,\frac{|a_{Np]}|}{s_{N}}\}$

现在，交换第p行和第k行，除非p=k。这也是为了保证变换后的矩阵U与初始矩阵A的对应元素相对大小一致。

按比例偏序选主元策略：

function [X] = P_G_R(A,b,n) %输入：系数矩阵A，常数矩阵b，n为系数矩阵A的阶数
AM=[A b];   %AM为增广矩阵
for c=1:n
    if AM(:,c)==0
        disp('该矩阵为奇异矩阵，不可逆');
        return
    else
        s=zeros(1,n-c+1);   %储存第c行到n行的所有每行中第c列的绝对值除以绝对值最大的元素，以方便按比例筛选
        for r=c:n
            s(1,r-c+1)=abs(AM(r,c))/max(abs(AM(r,c:n)));    %s的每个值计算公式
        end
        k=find(abs(s)==max(s));  %找到s中最大值所在位置
        k=k+c-1;    %k的值应该加上c行之前的元素间隔
        if k~=c     %如果最大行的位置与c行不一样，进行初等行变换中的交换两行的操作
            t=AM(c,:);
            AM(c,:)=AM(k,:);
            AM(k,:)=t;
        end
        for r=c+1:n    %高斯消元法化为上三角矩阵
            mr=AM(r,c)/AM(c,c);   %mr是使得第c行c列元素乘以之后与第r行c列元素相减等于零的值
            AM(r,c)=0;
            for cc=c+1:n+1
                AM(r,cc)=AM(r,cc)-mr*AM(c,cc);  %将r行中的cc列元素减去第c行的cc列元素的一个倍数，倍数由mr决定
            end
        end
    end
end
U=AM(1:n,1:n);  %将AM的n行n列内的所有元素记为U
Y=AM(:,n+1);    %将AM的所有行n+1列的所有元素记为Y
X=zeros(n,1);   %将解向量全部元素赋值0，则AX=b等价于UX=Y
for r=n:-1:1    %利用回代法计算解向量X的每一个值
    if r==n
        X(r,1)=Y(r,1)/U(r,r);   %计算第解向量X的n行1列处的值
    else
        sum=0;
        for rr=r+1:n
            sum=sum+U(r,rr)*X(rr,1);    %计算rr行到n行的解向量乘以r行rr列处对应系数
        end
        X(r)=(Y(r)-sum)/U(r,r);     %计算解向量X中r行处的值
    end
end
end

测试效果

测试系数矩阵A：

$\begin{pmatrix} 4& 8 & 4 &0 \\ 1& 5 & 4 &-3 \\ 1& 4 & 7 & 2\\ 1& 3 & 0 & -2 \end{pmatrix}$

测试常数项矩阵b：

$\begin{pmatrix} 8\\ -4\\ 10\\ -4 \end{pmatrix}$

测试结果：

总的来说，高斯消元法是求解线性方程组的最基本算法，它的计算复杂度为 $O(n^3)$ ，复杂度相对较高，而且在计算过程中的中间矩阵没有保存下来，这使得在科研过程中，科研人员更多地使用另一种数值算法，即下面即将介绍的三角分解法（PLU分解）。

2.PLU分解法：

2.1.PLU分解相对高斯消去法的优势

如总结所说，高斯消元法已经可以处理许多线性方程组了，但这个方法在实际中用得不多，原因在于计算复杂和没有保留中间矩阵以进一步研究矩阵性质。现在我们大致计算一下它的计算复杂度：

对循环

for c=1:n-1

...

r=c+1:n
mr=AM(r,c)/AM(c,c);
AM(r,c)=0;
for cc=r:n+1
AM(r,cc)=AM(r,cc)-mr*AM(c,cc);

...

对于c列来说，它需要进行n-c次除法来得到系数mr，在内循环里又需要进行n-r+2次减法和乘法的运算，所以需要循环：

$\sum_{c=1}^{n-1}\sum_{r=c+1}^{n}(n-r+2)$ 次

这个求和得出来的n是 $O(n^3)$ 的，计算复杂度相对较高。而用PLU分解法，在进行第一次矩阵分解的时候需要 $O(n^3)$ 次运算，在保存分解矩阵P，L，U后，仅换系数向量b而不改变A的情况下每次的运算只需要 $O(n^2)$ 次。并且可以通过P，L，U矩阵来研究系数矩阵A的性质，因此PLU分解法相比高斯消去法更常用。

2.2.PLU分解法原理

定理：如果A是非奇异矩阵，则存在一个置换矩阵P，使得PA存在三角分解：

$PA=LU$

其中P是由单位阵E经过有限次初等行变换中的交换变换得到的，L是主对角线元素全为1的下三角矩阵，U是主对角线不为零的上三角矩阵，形式如下:

$P = \left[ \begin{array}{cccc} 0 & \cdots & 0 & 1 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 \\ 1 & \cdots & 0 & 0 \\ \end{array} \right]$

注意这里只是给出P的其中一个可能形式，P的具体形式要根据给定的矩阵A来确定。

$L = \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ l_{21} & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ l_{n1} & l_{n2} & \cdots & 1 \\ \end{array} \right]$

$U = \left[ \begin{array}{cccc} u_{11} & u_{12} & \cdots & u_{1n} \\ 0 & u_{22} & \cdots & u_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & u_{nn} \\ \end{array} \right]$

定理的具体证明可参考高等代数教材。

2.3.PLU分解的代码实现（带冒泡法排序选主元方法）

function [L,U,P]=P_L_U(A,n)  %给入矩阵A，阶数n
P=eye(n);  %初始化P为单位阵
for c=1:n  
    % 部分选主元,按冒泡法降序排列每个元素，使得绝对值最大的在最上方，绝对值最小的元素在最下方
    for i=c:n    %冒泡法循环
        for j=c:n-i
            if abs(A(j,c))<abs(A(j+1,c))
                t=A(j,:);
                A(j,:)=A(j+1,:);
                A(j+1,:)=t;
                t=P(j,:);
                P(j,:)=P(j+1,:);
                P(j+1,:)=t;
            end
        end
    end
    % 检查主元是否为零  
    if A(c,c) == 0  
        error('Matrix is singular or too close to singular for this algorithm.');  
    end  
    % 前向消元，将c列对角线以下的元素都消为零，即高斯消元法过程。  
    for r=c+1:n  
        mr=A(r,c)/A(c,c);  
        A(r,c)=mr;  
        A(r,c+1:end)=A(r,c+1:end)-mr*A(c,c+1:end);  
    end  
end  
% 构建上三角矩阵U，注意此时AM已经包含了行交换  
U=A;
L=eye(n);
% 将U中L对应的部分置零，并且L继承U中置零部分 
for i = 1:n  
    for j=1:i-1  
        L(i,j)=U(i,j);
        U(i,j)=0;  
    end  
end
end

测试效果：

使用矩阵 $A=\begin{pmatrix} 1 & 1 & 0 & 4\\ 2& -1 &5 &0 \\ 5& 2 & 1 & 2\\ -3&0 & 2 & 6 \end{pmatrix}$ 来进行测试

结果：

用 $P^{-1}LU=A$ 来检测该三角分解是否正确，如图：

实际上，在matlab程序中，可以使用函数[L,U,P]=lu(A)来求得A的三角分解，也可以用lu函数与该函数比较，得出的结果一致。在这个程序中，我们实现将矩阵A进行三角分解成置换矩阵P，下三角矩阵L与上三角矩阵U，再进行一次前向替换法和回代法即可得到解X。推导过程如下：

$Ax=b\;\;\;\;\;\;\;\;\;\;\;PA=LU$

令 $y=Pb$ ，得到表达式： $LUx=y$ ，通过前向替换法得到： $Ux=L^{-1}y$ ，最后由回代法求得：

$x=U^{-1}L^{-1}y$

基于三角分解法求解x的代码实现部分：

function x=T_B_S(P,L,U,b)   %x是解向量，P是置换矩阵，L是下三角矩阵，U是上三角矩阵，b是系数向量。此代码用于求解经三角分解后的x向量值
    n=length(b);    %获取系数向量b的长度
    xx=zeros(n,1);  %构建x解向量的中间过程向量xx
    y=P*b;  %置换矩阵P*b得到新的系数向量y
    x=xx;
    for i=1:n   %前向替换法，在前面代码中写过，不再解释
        sum=0;
        if i==1
            xx(1,1)=y(1,1)/L(1,1);
        else
            for j=1:i-1
                sum=sum+L(i,j)*xx(j,1);
            end
            xx(i,1)=(y(i,1)-sum)/L(i,i);
        end
    end
    for i=n:-1:1   %回代法，在前面代码中写过，不再解释
        sum=0;
        if i==n
            x(n,1)=xx(n,1)/U(n,n);
        else
            for j=i+1:n
                sum=sum+U(i,j)*x(j,1);
            end
            x(i,1)=(xx(i,1)-sum)/U(i,i);
        end
    end
end

这样，通过PLU分解系数矩阵A，再利用前向替换法和回代法，可以求解出线性方程组的解。并且将矩阵A分解成一个上三角矩阵和下三角矩阵，若改变系数矩阵b，则不需要再重复高斯消元过程，节省了计算成本，也可以利用L和U矩阵来研究矩阵A的性质，故此方法更为广泛使用。同时指出，在MATLAB中，inv(A)和det(A)也利用三角分解法，例如，根据线性代数的理论，可以知道非奇异矩阵A的行列式等于 $(-1)^{q}*det(U)$ ，这里的U是矩阵A三角分解产生的上三角矩阵，而q是从单位矩阵E得到P所交换的行的次数。由于U是上三角矩阵，所以U的行列式是它的主对角线元素的乘积。

需要注意的是，Matlab的函数不允许改变给入参数的值，虽然代码充分利用给入矩阵A来进行储存矩阵L与U的值，但是实际上A原本的值并未改变，Matlab自动申请一个内存空间储存L与U的值，这造成了内存浪费，因此在用实际工程中使用三角分解时，最好用C或者Fotran来进行三角分解。

四、最后总结：

本文简要介绍了两种方法的原理和代码实现。线性方程组的一般解法思路是将系数矩阵，通过高斯消去法转化为一个上三角矩阵，最后利用回代法求解得出线性方程组的数值解。或者通过三角分解法，将系数矩阵转化为一个下三角矩阵和一个上三角矩阵相乘的形式。前者因为计算复杂度较高，每给出一个新的矩阵都会进行 $O(n^3)$ 运算才能得出结果，后者仅第一次需要 $O(n^3)$ 次运算，当仅改变系数向量b而不改变A时，所需要的计算复杂度是 $O(n^2)$ 次，并且保留下来的矩阵L和U可以用来研究矩阵A的性质（如行列式或A的迹等），因此在实际研究中，三角分解法被应用得更多。

努力上进的math boy

关注

48
点赞
踩
56

收藏

觉得还不错? 一键收藏
1
评论
[数值方法]线性方程组Ax=b的高斯消元法与三角分解法原理和代码实现-MatLab

本文简要介绍了一般线性方程组的数值解法，简要推导原理和给出代码实现，并通过计算算法复杂度，进一步分析矩阵A的性质来对比高斯消去法和PLU分解法的优劣。
复制链接

扫一扫