Matlab软件实现算法运算

最新推荐文章于 2024-09-11 12:24:03 发布

原创

最新推荐文章于 2024-09-11 12:24:03 发布 · 684 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#图像处理

这篇博客介绍了如何在Matlab中使用龙格-库塔方法和变步长欧拉方法进行算法运算。首先展示了积分一步的变步长龙格-库塔方法的代码及其运算结果，接着详细阐述了积分一步的变步长欧拉方法的实现过程，并给出了相应的代码和运算结果。

（1）积分一步的变步长龙格-库塔方法
题目：在这里插入图片描述
代码：function chap1_RungeKutta_method
% test the Runge-Kutta method for ODE IVP% foundate = ‘2015-3-8’;% chgedate = ‘2020-04-30’;% by Zhang, Xupingu0 = 1;T = 1;h = 0.1;N = T/h;t = 0:h:T;solu = exact1(t);f = @f1;u_euler = euler(f,u0,t,h,N);u_RK = runge_kutta_44(f,u0,t,h,N);
运算结果：
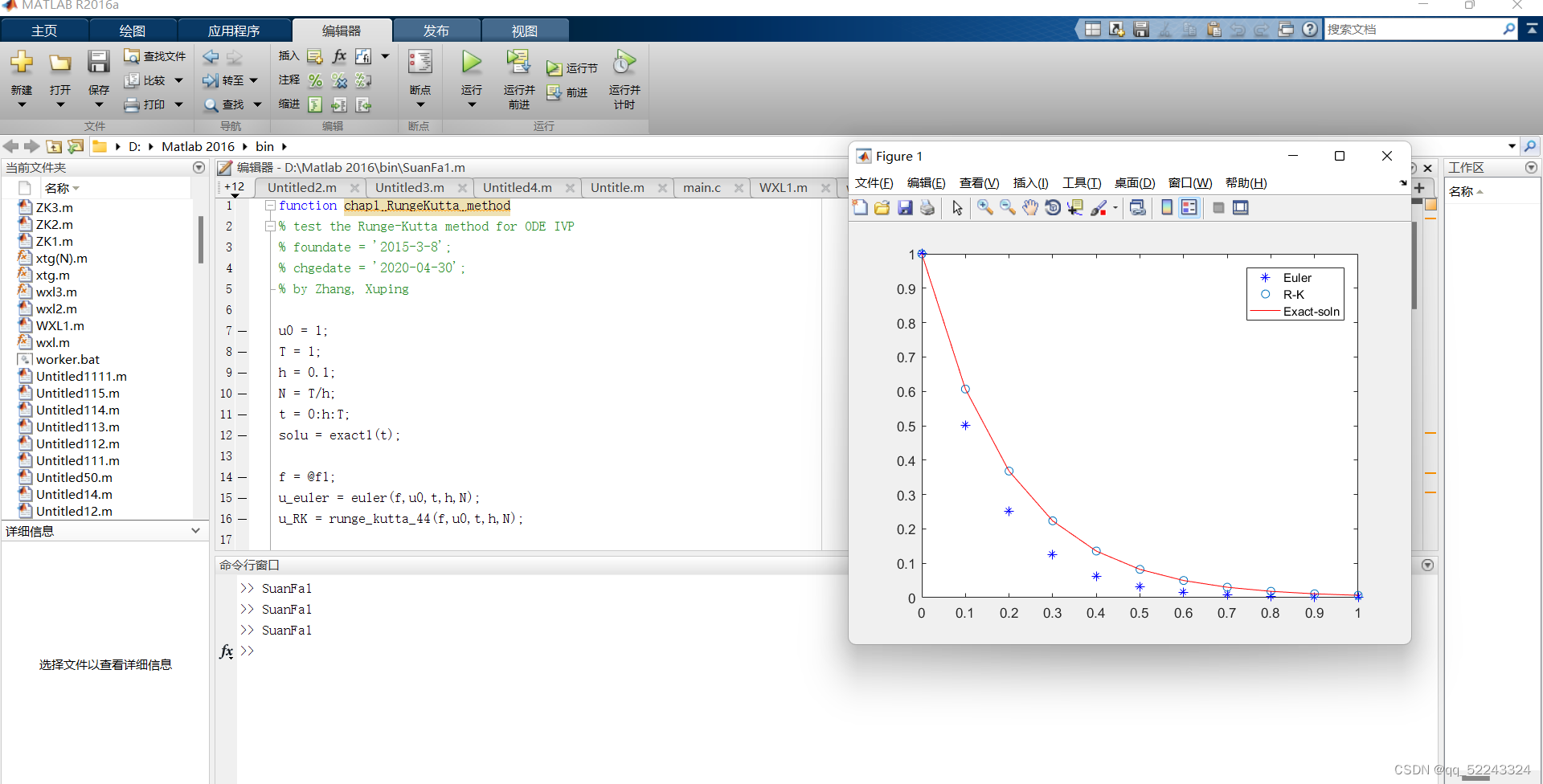在这里插入图片描述（2）积分一步的变步长欧拉方法
题目：
代码：clear;
format long;a = 0;b = 1;h = 0.1;d = 1;res = forward(a, b, h, d);x = res(1,:);y = res(2,:);z = [1, 1.0954, 1.1832, 1.2649, 1.3416, 1.4142, 1.4832, 1.5492, 1.6125, 1.6733, 1.7321];y(2,:) = z;plot(x, y);function result = forward(a, b, h, y) n = (b-a)/h; x0 = a; x1 = a; y0 = y; result(1,1) = x0; result(2,1) = y0; for m = 0:n-