1、前言
特征转换的基本思想是，数据集的原始特征是数据点的描述符/特点，也应该能创造一组新的特征，用更少的列来解释数据点，并且效果不变，甚至更好。
特征选择和特征转换都是降维的好办法，但是它们的方法迥然不同。
- 特征选择仅限于从原始列中选择特征；特征转换算法则将原始列组合起来，从而创建可以更好地描述数据的特征。因此，特征选择的降维原理是隔离信号列和忽略噪声列。
- 特征转换方法使用原始数据集的隐藏结构创建新的列，生成一个全新的数据集，结构与之前不同。这些算法创建的新特征非常强大，只需要几个就可以准确地解释整个数据集。
特征转换的原理是生成可以捕获数据本质的新特征，这一点和特征构造的本质类似：都是创建新特征，捕捉数据的潜在结构。特征构造用几个列之间的简单操作（加法和乘法等）构造新的列。经典特征构造过程构造出的任何特征都只能用原始数据集中的几个列生成。
2、基础知识讲解
2.1主成分分析（PCA）
主成分分析（PCA，principal components analysis）是将有多个相关特征的数据集投影到相关特征较少的坐标系上。这些新的、不相关的特征叫主成分。主成分能替代原始特征空间的坐标系，需要的特征少、捕捉的变化多。
主成分分析是无监督算法。主成分按可以解释的方差来排序，第一个主成分最能解释数据的方差，第二个其次。
PCA过程:
- 创建数据集的协方差矩阵
- 计算协方差矩阵的特征值
- 保留前k个特征值（按特征值降序排列）
- 用保留的特征向量转换新的数据点。
鸢尾花数据集
鸢尾花数据集（iris）有150行和4列。每行代表一朵花，每列代表花的4种定量特点。数据集的目标是拟合一个分类器，尝试在给定4个特征后，在3种花中预测。花的类型分别是山鸢尾（setosa）、变色鸢尾（versicolor）和维吉尼亚鸢尾（virginica）。
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
# 加载数据集
iris = load_iris()
# 创建X和y变量，存储特征和响应列
iris_X, iris_y = iris.data, iris.target
# 要预测的花的名称
iris.target_namesarray(['setosa', 'versicolor', 'virginica'], dtype='<U10')
# 特征名称
iris.feature_names['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
def plot(X, y, title, x_label, y_label):
ax = plt.subplot(111)
for label,marker,color in zip(range(3),('^', 's', 'o'),
('blue', 'red', 'green')):
plt.scatter(x=X[:,0].real[y == label],
y=X[:,1].real[y == label],
color=color,
alpha=0.5,
label=label_dict[label])
plt.xlabel(x_label)
plt.ylabel(y_label)
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
# {0: 'setosa', 1: 'versicolor', 2: 'virginica'}
label_dict = {i: k for i, k in enumerate(iris.target_names)}
plot(iris_X, iris_y, "Original Iris Data", "sepal length (cm)", "sepal width (cm)")
创建数据集的协方差矩阵
# 手动计算PCA
import numpy as np
# 计算均值向量
mean_vector = iris_X.mean(axis=0)
print(mean_vector)
# 计算协方差矩阵
cov_mat = np.cov((iris_X).T)
cov_mat.shape[5.84333333 3.05733333 3.758 1.19933333]
(4, 4)
计算协方差矩阵的特征值
# 计算鸢尾花数据集的特征向量和特征值
eig_val_cov, eig_vec_cov = np.linalg.eig(cov_mat)
# 按降序打印特征向量和相应的特征值
for i in range(len(eig_val_cov)):
eigvec_cov = eig_vec_cov[:,i]
print('Eigenvector {}: \n{}'.format(i+1, eigvec_cov))
print('Eigenvalue {} from covariance matrix: {}'.format(i+1, eig_val_cov[i]))
print(30 * '-')Eigenvector 1: [ 0.36138659 -0.08452251 0.85667061 0.3582892 ] Eigenvalue 1 from covariance matrix: 4.228241706034865 ------------------------------ Eigenvector 2: [-0.65658877 -0.73016143 0.17337266 0.07548102] Eigenvalue 2 from covariance matrix: 0.24267074792863372 ------------------------------ Eigenvector 3: [-0.58202985 0.59791083 0.07623608 0.54583143] Eigenvalue 3 from covariance matrix: 0.07820950004291922 ------------------------------ Eigenvector 4: [ 0.31548719 -0.3197231 -0.47983899 0.75365743] Eigenvalue 4 from covariance matrix: 0.02383509297344936 ------------------------------
np.dot(cov_mat,eig_vec_cov[:,0])array([ 1.52802986, -0.35738162, 3.62221038, 1.51493333])
np.dot(eig_val_cov[0],eig_vec_cov[:,0])array([ 1.52802986, -0.35738162, 3.62221038, 1.51493333])
按降序保留前K个特征值
碎石图是一种简单的折线图，显示每个主成分解释数据总方差的百分比。要绘制碎石图，需要对特征值进行降序排列，绘制每个主成分和之前所有主成分方差的和。
# 每个主成分解释的百分比是特征值除以特征值之和
explained_variance_ratio = eig_val_cov/eig_val_cov.sum()
explained_variance_ratioarray([0.92461872, 0.05306648, 0.01710261, 0.00521218])
# 碎石图
plt.plot(np.cumsum(explained_variance_ratio))
plt.title('Scree Plot')
plt.xlabel('Principal Component (k)')
plt.ylabel('% of Variance Explained <= k')
保留特征向量转换新的数据点
# 保存两个特征向量
top_2_eigenvectors = eig_vec_cov[:,:2].T
# 转置，每行是一个主成分，两行代表两个主成分
top_2_eigenvectorsarray([[ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ],
[-0.65658877, -0.73016143, 0.17337266, 0.07548102]])
# 将数据集从150 x 4转换到150 x 2
# 将数据矩阵和特征向量相乘
np.dot(iris_X, top_2_eigenvectors.T)[:5,]array([[ 2.81823951, -5.64634982],
[ 2.78822345, -5.14995135],
[ 2.61337456, -5.18200315],
[ 2.75702228, -5.0086536 ],
[ 2.7736486 , -5.65370709]])
scikit-learn的PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
# 在数据上使用PCA
pca.fit(iris_X)PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
pca.components_array([[ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ],
[ 0.65658877, 0.73016143, -0.17337266, -0.07548102]])
pca.transform(iris_X)[:5,]array([[-2.68412563, 0.31939725],
[-2.71414169, -0.17700123],
[-2.88899057, -0.14494943],
[-2.74534286, -0.31829898],
[-2.72871654, 0.32675451]])
这里投影后的数据和之前不同，因为scikit-learn的PCA会在预测阶段自动将数据中心化，从而改变结果。
# 手动中心化数据，模仿scikit-learn的PCA
np.dot(iris_X-mean_vector, top_2_eigenvectors.T)[:5,]array([[-2.68412563, -0.31939725],
[-2.71414169, 0.17700123],
[-2.88899057, 0.14494943],
[-2.74534286, 0.31829898],
[-2.72871654, -0.32675451]])
# 绘制原始和投影后的数据
plot(iris_X, iris_y, "Original Iris Data", "sepal length (cm)", "sepal width (cm)")
plt.show()
plot(pca.transform(iris_X), iris_y, "Iris: Data projected onto first two PCA components", "PCA1", "PCA2")
# 每个主成分解释的方差百分比,和之前的一样
pca.explained_variance_ratio_array([0.92461872, 0.05306648])
PCA的主要优点之一是消除相关特征。本质上，在特征值分解时，得到的所有主成分都互相垂直,彼此线性无关。
# 原始数据集的相关矩阵
np.corrcoef(iris_X.T)array([[ 1. , -0.11756978, 0.87175378, 0.81794113],
[-0.11756978, 1. , -0.4284401 , -0.36612593],
[ 0.87175378, -0.4284401 , 1. , 0.96286543],
[ 0.81794113, -0.36612593, 0.96286543, 1. ]])
np.corrcoef(iris_X.T)[[0, 0, 0, 1, 1], [1, 2, 3, 2, 3]]array([-0.11756978, 0.87175378, 0.81794113, -0.4284401 , -0.36612593])
# 原始数据集的平均相关性
np.corrcoef(iris_X.T)[[0, 0, 0, 1, 1], [1, 2, 3, 2, 3]].mean()0.1555118162316355
# 取所有主成分
full_pca = PCA(n_components=4)
# PCA拟合数据集
full_pca.fit(iris_X)PCA(copy=True, iterated_power='auto', n_components=4, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
pca_iris = full_pca.transform(iris_X)
# PCA后的平均相关系数
np.corrcoef(pca_iris.T)[[0, 0, 0, 1, 1], [1, 2, 3, 2, 3]].mean()
# 非常接近0，因为列互相独立7.913820960116712e-16
中心化和缩放对PCA的影响
scikit-learn的PCA在预测阶段会将数据进行中心化（centering）
将数据中心化不会影响主成分
# 导入缩放模块
from sklearn.preprocessing import StandardScaler
# 中心化数据 with_std：s是训练样本的标准偏差，如果with_std = False，则为1
X_centered = StandardScaler(with_std=False).fit_transform(iris_X)
X_centered[:5,]array([[-0.74333333, 0.44266667, -2.358 , -0.99933333],
[-0.94333333, -0.05733333, -2.358 , -0.99933333],
[-1.14333333, 0.14266667, -2.458 , -0.99933333],
[-1.24333333, 0.04266667, -2.258 , -0.99933333],
[-0.84333333, 0.54266667, -2.358 , -0.99933333]])
# 绘制中心化后的数据集
plot(X_centered, iris_y, "Iris: Data Centered", "sepal length (cm)", "sepal width (cm)")
# 拟合数据集
pca.fit(X_centered)PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
# 主成分一样
pca.components_array([[ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ],
[ 0.65658877, 0.73016143, -0.17337266, -0.07548102]])
# PCA自动进行中心化，投影一样
pca.transform(X_centered)[:5,]array([[-2.68412563, 0.31939725],
[-2.71414169, -0.17700123],
[-2.88899057, -0.14494943],
[-2.74534286, -0.31829898],
[-2.72871654, 0.32675451]])
# PCA中心化后的数据图，和之前的一样
plot(pca.transform(X_centered), iris_y, "Iris: Data projected onto first two PCA components with centered data", "PCA1", "PCA2")
# 每个主成分解释方差的百分比
pca.explained_variance_ratio_array([0.92461872, 0.05306648])
原始矩阵和中心化后矩阵的协方差矩阵相同。如果两个矩阵的协方差矩阵相同，那么它们的特征值分解也相同。因此，scikit-learn的PCA不会对数据进行中心化，因为无论是否进行中心化操作，结果都一样
# z分数缩放
X_scaled = StandardScaler().fit_transform(iris_X)
# 绘图
plot(X_scaled, iris_y, "Iris: Data Scaled", "sepal length (cm)", "sepal width (cm)")
# 二维PCA拟合
pca.fit(X_scaled)
# 与中心化后的主成分不同
pca.components_array([[ 0.52106591, -0.26934744, 0.5804131 , 0.56485654],
[ 0.37741762, 0.92329566, 0.02449161, 0.06694199]])
对数据进行中心化，并除以标准差后，发现主成分发生变化
# 缩放不同 投影不同
pca.transform(X_scaled)[:5,]array([[-2.26470281, 0.4800266 ],
[-2.08096115, -0.67413356],
[-2.36422905, -0.34190802],
[-2.29938422, -0.59739451],
[-2.38984217, 0.64683538]])
# 每个主成分解释方差的百分比
pca.explained_variance_ratio_array([0.72962445, 0.22850762])
第一个主成分解释方差的比例比之前低得多,这是因为对数据进行缩放后，列与列的协方差会更加一致，而且每个主成分解释的方差会变得分散，而不是集中在一个主成分中
# 绘制缩放后数据的PCA
plot(pca.transform(X_scaled), iris_y, "Iris: Data projected onto first two PCA components", "PCA1", "PCA2")
深入解释主成分
# 解释主成分 鸢尾花数据集是一个150×4
pca.components_ # 2 x 4 矩阵array([[ 0.52106591, -0.26934744, 0.5804131 , 0.56485654],
[ 0.37741762, 0.92329566, 0.02449161, 0.06694199]])
# 原始矩阵 (150 x 4) 和转置主成分矩阵 (4 x 2) 相乘 得到投影数据 (150 x 2)
np.dot(X_scaled, pca.components_.T)[:5,]array([[-2.26470281, 0.4800266 ],
[-2.08096115, -0.67413356],
[-2.36422905, -0.34190802],
[-2.29938422, -0.59739451],
[-2.38984217, 0.64683538]])
# 提取缩放数据的第一行
first_scaled_flower = X_scaled[0]
# 提取两个主成分
first_Pc = pca.components_[0]
second_Pc = pca.components_[1]
first_scaled_flower.shape # (4,)
print(first_scaled_flower) # array([-0.90068117, 1.03205722, -1.3412724 , -1.31297673])
# 第一行和主成分的点积
np.dot(first_scaled_flower, first_Pc), np.dot(first_scaled_flower, second_Pc)[-0.90068117 1.01900435 -1.34022653 -1.3154443 ]
(-2.2647028088075887, 0.4800265965209873)
# PCA的转换方法
pca.transform(X_scaled)[:5,]array([[-2.26470281, 0.4800266 ],
[-2.08096115, -0.67413356],
[-2.36422905, -0.34190802],
[-2.29938422, -0.59739451],
[-2.38984217, 0.64683538]])
# 删掉后两个特征，使可视化更简单
iris_2_dim = iris_X[:,2:4]
# 中心化
iris_2_dim = iris_2_dim - iris_2_dim.mean(axis=0)
plot(iris_2_dim, iris_y, "Iris: Only 2 dimensions", "sepal length", "sepal width")
# 实例化保留两个主成分的PCA
twodim_pca = PCA(n_components=2)
# 拟合并转换截断的数据
iris_2_dim_transformed = twodim_pca.fit_transform(iris_2_dim)
plot(iris_2_dim_transformed, iris_y, "Iris: PCA performed on only 2 dimensions", "PCA1", "PCA2")
将主成分理解成引导向量，展示数据如何移动，以及这些向量如何变成垂直坐标系
# 下面的代码展示原始数据和用PCA投影后的数据
# 但是在图上，每个主成分都按数据的向量处理
# 长箭头是第一个主成分，短箭头是第二个
def draw_vector(v0, v1, ax):
arrowprops=dict(arrowstyle='->',linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
fig, ax = plt.subplots(2, 1, figsize=(10, 10))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
# 绘图 原始数据
ax[0].scatter(iris_2_dim[:, 0], iris_2_dim[:, 1], alpha=0.2)
for length, vector in zip(twodim_pca.explained_variance_, twodim_pca.components_):
v = vector * np.sqrt(length) # 拉长向量，和explained_variance对应
draw_vector(twodim_pca.mean_,
twodim_pca.mean_ + v, ax=ax[0])
ax[0].set(xlabel='x', ylabel='y', title='Original Iris Dataset',
xlim=(-3, 3), ylim=(-2, 2))
# 转换后的数据
ax[1].scatter(iris_2_dim_transformed[:, 0], iris_2_dim_transformed[:, 1], alpha=0.2)
# explained_variance_:降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
for length, vector in zip(twodim_pca.explained_variance_, twodim_pca.components_):
transformed_component = twodim_pca.transform([vector])[0] # 转换到新坐标系
v = transformed_component * np.sqrt(length) # 拉长向量，和explained_variance对应
draw_vector(iris_2_dim_transformed.mean(axis=0),
iris_2_dim_transformed.mean(axis=0) + v, ax=ax[1])
ax[1].set(xlabel='component 1', ylabel='component 2',
title='Projected Data',
xlim=(-3, 3), ylim=(-1, 1))
2.2线性判别分析(LDA)
LDA是特征变换算法，也是有监督分类器。和PCA一样，LDA的目标是提取一个新的坐标系，将原始数据集投影到一个低维空间中。和PCA的主要区别在于，LDA不会专注于数据的方差，而是优化低维空间，以获得最佳的类别可分性。新的坐标系在为分类模型查找决策边界时更有用，LDA非常适合用于构建分类流水线。
工作原理:
- 计算每个类别的均值向量
- 计算类内和类间的散布矩阵
- 计算
的特征值和特征向量
- 降序排列特征值，保留前k个特征向量
- 使用前几个特征向量将数据投影到新空间
计算每个类别的均值向量
# 每个类别的均值向量
# 将鸢尾花数据集分成3块
# 每块代表一种鸢尾花，计算均值
mean_vectors = []
for cl in [0, 1, 2]:
class_mean_vector = np.mean(iris_X[iris_y==cl], axis=0)
mean_vectors.append(class_mean_vector)
print(label_dict[cl], class_mean_vector)setosa [5.006 3.428 1.462 0.246] versicolor [5.936 2.77 4.26 1.326] virginica [6.588 2.974 5.552 2.026]
计算类内和类间的散布矩阵
:类内的散布矩阵
:类间的散布矩阵
m是数据集的总体均值,mi是每个类别的样本均值,Ni是每个类别的样本大小
# 类内散布矩阵
S_W = np.zeros((4,4))
# 对于每种鸢尾花
for cl,mv in zip([0, 1, 2], mean_vectors):
# 从0开始，每个类别的散布矩阵
class_sc_mat = np.zeros((4,4))
# 对于每个样本
for row in iris_X[iris_y == cl]:
# 列向量
row, mv = row.reshape(4,1), mv.reshape(4,1)
# 4 x 4的矩阵
class_sc_mat += (row-mv).dot((row-mv).T)
# 散布矩阵的和
S_W += class_sc_mat
S_Warray([[38.9562, 13.63 , 24.6246, 5.645 ],
[13.63 , 16.962 , 8.1208, 4.8084],
[24.6246, 8.1208, 27.2226, 6.2718],
[ 5.645 , 4.8084, 6.2718, 6.1566]])
# 类间散布矩阵
# 数据集的均值
overall_mean = np.mean(iris_X, axis=0).reshape(4,1)
# 会变成散布矩阵
S_B = np.zeros((4,4))
for i,mean_vec in enumerate(mean_vectors):
# 每种花的数量
n = iris_X[iris_y==i,:].shape[0]
# 每种花的列向量
mean_vec = mean_vec.reshape(4,1)
S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
S_Barray([[ 63.21213333, -19.95266667, 165.2484 , 71.27933333],
[-19.95266667, 11.34493333, -57.2396 , -22.93266667],
[165.2484 , -57.2396 , 437.1028 , 186.774 ],
[ 71.27933333, -22.93266667, 186.774 , 80.41333333]])
计算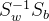
的特征值和特征向量
# 计算矩阵的特征值和特征向量
eig_vals, eig_vecs = np.linalg.eig(np.dot(np.linalg.inv(S_W), S_B))
eig_vecs = eig_vecs.real
eig_vals = eig_vals.real
for i in range(len(eig_vals)):
eigvec_sc = eig_vecs[:,i]
print('Eigenvector {}: {}'.format(i+1, eigvec_sc))
print('Eigenvalue {:}: {}'.format(i+1, eig_vals[i]))
printEigenvector 1: [ 0.20874182 0.38620369 -0.55401172 -0.7073504 ] Eigenvalue 1: 32.19192919827802 Eigenvector 2: [-0.00653196 -0.58661055 0.25256154 -0.76945309] Eigenvalue 2: 0.28539104262306414 Eigenvector 3: [ 0.85279432 -0.19031287 -0.14958685 -0.4627598 ] Eigenvalue 3: 3.776351867410287e-15 Eigenvector 4: [-0.39246717 0.43081663 0.48378685 -0.65292943] Eigenvalue 4: -4.655575776665808e-15
注意第三个和第四个特征值几乎是0，这是因为LDA的工作方式是在类间划分决策边界。考虑到鸢尾花数据中只有3个类别，我们可能只需要2个决策边界。通常来说，用LDA拟合n个类别的数据集，最多只需要n-1次切割。
降序排列特征值，保留前k个特征向量
# 保留最好的两个线性判别式
linear_discriminants = eig_vecs.T[:2]
linear_discriminantsarray([[ 0.20874182, 0.38620369, -0.55401172, -0.7073504 ],
[-0.00653196, -0.58661055, 0.25256154, -0.76945309]])
# 解释总方差的比例
eig_vals / eig_vals.sum()array([ 9.91212605e-01, 8.78739503e-03, 1.16276584e-16, -1.43348520e-16])
使用前几个特征向量投影到新空间
# LDA投影数据
lda_iris_projection = np.dot(iris_X, linear_discriminants.T)
lda_iris_projection[:5,]
plot(lda_iris_projection, iris_y, "LDA Projection", "LDA1", "LDA2")
在scikit-learn中使用LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 实例化LDA模块
lda = LinearDiscriminantAnalysis(n_components=2)
# 拟合并转换鸢尾花数据,注意和PCA不同，需要iris_y
X_lda_iris = lda.fit_transform(iris_X, iris_y)
# 绘制投影数据
plot(X_lda_iris, iris_y, "LDA Projection", "LDA1", "LDA2")
# 和pca.components_基本一样 但是转置了 (4x2，而不是2x4)
lda.scalings_array([[ 0.82937764, 0.02410215],
[ 1.53447307, 2.16452123],
[-2.20121166, -0.93192121],
[-2.81046031, 2.83918785]])
# 和手动计算一样
lda.explained_variance_ratio_array([0.9912126, 0.0087874])
# scikit-learn计算的结果和手动一样，但是有缩放
for manual_component, sklearn_component in zip(eig_vecs.T[:2], lda.scalings_.T):
print(sklearn_component / manual_component)[3.97322221 3.97322221 3.97322221 3.97322221] [-3.68987776 -3.68987776 -3.68987776 -3.68987776]
# 用LDA拟合缩放数据
X_lda_iris = lda.fit_transform(X_scaled, iris_y)
lda.scalings_ # 缩放后数据的尺度不同array([[ 0.68448644, 0.01989153],
[ 0.66659193, 0.94029176],
[-3.87282074, -1.63962597],
[-2.13508598, 2.15691008]])
# 在截断的数据集上拟合
iris_2_dim_transformed_lda = lda.fit_transform(iris_2_dim, iris_y)
# 投影数据
iris_2_dim_transformed_lda[:5,]array([[-6.0424185 , 0.05692487],
[-6.0424185 , 0.05692487],
[-6.19685555, 0.27304711],
[-5.88798144, -0.15919736],
[-6.0424185 , 0.05692487]])
# 名称不同
components = lda.scalings_.T # 转置为和PCA一样，行变成主成分
print(components)[[ 1.54437053 2.40239438] [-2.16122235 5.04259916]]
np.dot(iris_2_dim, components.T)[:5,] # 和transform一样array([[-6.0424185 , 0.05692487],
[-6.0424185 , 0.05692487],
[-6.19685555, 0.27304711],
[-5.88798144, -0.15919736],
[-6.0424185 , 0.05692487]])
# 原始特征的相关性很大
np.corrcoef(iris_2_dim.T)array([[1. , 0.96286543],
[0.96286543, 1. ]])
# LDA的相关性极小，和PCA一样
np.corrcoef(iris_2_dim_transformed_lda.T)array([[1.0000000e+00, 9.2031405e-16],
[9.2031405e-16, 1.0000000e+00]])
# 下面的代码展示原始数据和用LDA投影后的数据
# 但是在图上，每个都按数据的向量处理
# 长箭头是第一个主成分，短箭头是第二个
def draw_vector(v0, v1, ax):
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
fig, ax = plt.subplots(2, 1, figsize=(10, 10))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
# 绘图
ax[0].scatter(iris_2_dim[:, 0], iris_2_dim[:, 1], alpha=0.2)
for length, vector in zip(lda.explained_variance_ratio_, components):
v = vector * .5
draw_vector(lda.xbar_, lda.xbar_ + v, ax=ax[0]) # lda.xbar_ 等于 pca.mean_
ax[0].axis('equal')
ax[0].set(xlabel='x', ylabel='y', title='Original Iris Dataset',
xlim=(-3, 3), ylim=(-3, 3))
ax[1].scatter(iris_2_dim_transformed_lda[:, 0], iris_2_dim_transformed_lda[:, 1], alpha=0.2)
for length, vector in zip(lda.explained_variance_ratio_, components):
transformed_component = lda.transform([vector])[0]
v = transformed_component * .1
draw_vector(iris_2_dim_transformed_lda.mean(axis=0), iris_2_dim_transformed_lda.mean(axis=0) + v, ax=ax[1])
ax[1].axis('equal')
ax[1].set(xlabel='lda component 1', ylabel='lda component 2',
title='Linear Discriminant Analysis Projected Data',
xlim=(-10, 10), ylim=(-3, 3))
2.3LDA和PCA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score
import warnings
warnings.filterwarnings('ignore')
# 创建有一个主成分的PCA模块
single_pca = PCA(n_components=1)
# 创建有一个判别式的LDA模块
single_lda = LinearDiscriminantAnalysis(n_components=1)
# 实例化KNN模型
knn = KNeighborsClassifier(n_neighbors=3)
# 不用特征转换，用KNN进行交叉检验
knn_average = cross_val_score(knn, iris_X, iris_y).mean()
# 这是基线准确率。如果什么也不做，KNN的准确率是98%
knn_average
# 0.9803921568627452
lda_pipeline = Pipeline([('lda', single_lda), ('knn', knn)])
lda_average = cross_val_score(lda_pipeline, iris_X, iris_y).mean()
# 比PCA好，比原始的差
lda_average
# 0.9673202614379085
# 创建执行PCA的流水线
pca_pipeline = Pipeline([('pca', single_pca), ('knn', knn)])
pca_average = cross_val_score(pca_pipeline, iris_X, iris_y).mean()
pca_average
# 0.8941993464052288
# 试试有两个判别式的LDA
lda_pipeline = Pipeline([('lda', LinearDiscriminantAnalysis(n_components=2)),
('knn', knn)])
lda_average = cross_val_score(lda_pipeline, iris_X, iris_y).mean()
# 和原来的一样
lda_average
# 0.9803921568627452
# 用特征选择工具和特征转换工具做对比
from sklearn.feature_selection import SelectKBest
# 尝试所有的k值，但是不包括全部保留
for k in [1, 2, 3]:
# 构建流水线
select_pipeline = Pipeline([('select', SelectKBest(k=k)), ('knn', knn)])
# 交叉检验流水线
select_average = cross_val_score(select_pipeline, iris_X, iris_y).mean()
print(k, "best feature has accuracy:", select_average)
# 1 best feature has accuracy: 0.9538398692810457
# 2 best feature has accuracy: 0.9607843137254902
# 3 best feature has accuracy: 0.9738562091503268
def get_best_model_and_accuracy(model, params, X, y):
grid = GridSearchCV(model, # 网格搜索的模型
params, # 试验的参数
error_score=0.) # 如果出错，当作结果是0
grid.fit(X, y) # 拟合模型和参数
# 传统的性能指标
print("Best Accuracy: {}".format(grid.best_score_))
# 最好参数
print("Best Parameters: {}".format(grid.best_params_))
# 平均拟合时间（秒
print("Average Time to Fit (s): {}".format(round(grid.cv_results_['mean_fit_time'].mean(), 3)))
# 平均预测时间（秒）
# 显示模型在实时分析中的性能
print("Average Time to Score (s): {}".format(round(grid.cv_results_['mean_score_time'].mean(), 3)))
from sklearn.model_selection import GridSearchCV
iris_params = {
'preprocessing__scale__with_std': [True, False],
'preprocessing__scale__with_mean': [True, False],
'preprocessing__pca__n_components':[1, 2, 3, 4],
# 根据scikit-learn文档，LDA的最大n_components是类别数减1
'preprocessing__lda__n_components':[1, 2],
'clf__n_neighbors': range(1, 9)
}
# 更大的流水线
preprocessing = Pipeline([('scale', StandardScaler()),
('pca', PCA()),
('lda', LinearDiscriminantAnalysis())])
iris_pipeline = Pipeline(steps=[('preprocessing', preprocessing),
('clf', KNeighborsClassifier())])
get_best_model_and_accuracy(iris_pipeline, iris_params, iris_X, iris_y)
# Best Accuracy: 0.9866666666666667
# Best Parameters: {'clf__n_neighbors': 3, 'preprocessing__lda__n_components': 2, 'preprocessing__pca__n_components': 3, 'preprocessing__scale__with_mean': True, 'preprocessing__scale__with_std': False}
# Average Time to Fit (s): 0.001
# Average Time to Score (s): 0.0013、总结
我们深入研究了线性判别分析（LDA）和主成分分析（PCA）这两个强大的工具，它们对于降维和特征提取在某些情境下非常有效。然而，我们也意识到它们存在的局限性，主要体现在它们是线性转换方法，只能创造线性的边界。
LDA 和 PCA 总结：
线性判别分析（LDA）：LDA 是一种有监督的降维方法，旨在最大化类别间的差异，同时最小化类别内的差异。它在分类问题中经常被用于降低维度。
主成分分析（PCA）：PCA 是一种无监督的降维方法，通过找到数据中的主成分（方差最大的方向），将数据投影到较低维度的子空间中。它常用于去除冗余信息和降低噪声。
局限性：
线性转换： LDA 和 PCA 都是线性转换方法，只能捕捉数据中的线性关系，难以处理非线性结构的数据。
扫一扫
3499
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
