离散数学作业-总集

作业day-1

1、学习数学表达式的困难
（1） 下标混用，以及不够用，下标表示出现逻辑问题；
$$\underset{M}{\min }{\left(\sum _{j=1}^{n-1}{\alpha }_j{y}_j-y_i\right)}^2$$
该式中$\sum$部分想描述n个预测中除第$i$个预测外其他预测的加权和，而该式表达不清晰，可能存在着$i==j$的情况.
（2）向量数值不分；

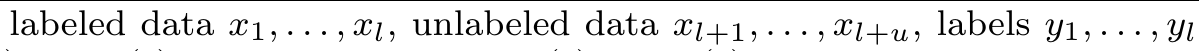
此处x应为$\mathbf{x}$

（3）表达式全篇未统一。


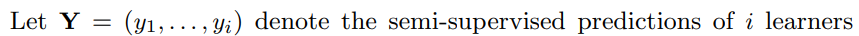
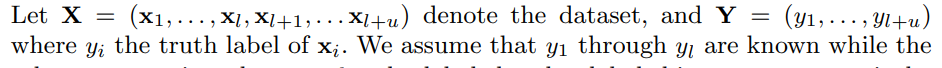
同一个符号两个不同的定义。
2、 令 A = { 3 , 5 } \mathbf{A}=\{3,5\} A={3,5}，写出$2^{\mathbf{A}}$

2 A = { ∅ , { 3 } , { 5 } , { 3 , 5 } } 2^{\mathbf{A}}=\{\emptyset, \{3\}, \{5\}, \{3,5\} \} 2A={∅,{3},{5},{3,5}}.

3、展开$2^{\varnothing }$

2 ∅ = { ∅ } 2^{\emptyset}=\{\emptyset\} 2∅={∅}.

4、令 A = { 5 , 6 , 7 , 8 , 9 } \mathbf{A}=\{5,6,7,8,9\} A={5,6,7,8,9}写出另外两种表达式
方法1-枚举法： A = { 5 , … , 9 } \mathbf{A} =\{5,\dots,9\} A={5,…,9}. code:\mathbf{A} = {5, \dots, 9}
方法2-谓词法： A = { x ∈ N ∣ 4 < x < 10 } \mathbf{A} = \{x \in \mathbb{N}| 4< x < 10 \} A={x∈N∣4<x<10}. code:\mathbf{A} = {x \in \mathbb{N}| 4< x < 10 }

7、Deep multi-view的符号错误
（1）自变量x可能是$\mathbf{x}$；
${\mathbf{X}}^{(m)}=\left[x_1^{(m)},\cdots ,x_N^{(m)}\right]$

(2) 该用数学模式时并未使用;

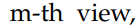
(3) m与M混用;
$$\begin{gathered} {\mathbf{X}}^{(m)}=\left[x_1^{(m)},\cdots ,x_N^{(m)}\right] \\ {F}_1\left({\mathbf{X}}^{(1)}\right),\cdots ,F_M\left({\mathbf{X}}^{(M)}\right) \end{gathered}$$
(4) $\sum$ 没有上界;
$${\mathcal{L}}^p(x,i)=-\log \frac{\exp (x[i])}{{\sum }_j\exp (x[j])}$$

(5) ${\mathbf{Y}}_{ij}$前后均未给出明确定义.
$$\mathcal{L}(\mathbf{I},\mathbf{Y})={\mathbf{Y}}_{ij}\cdot \log \left\{{\mathcal{E}}_m(\mathcal{F}(\mathbf{I})\}\cdot \left(\rho (\mathbf{I})+\alpha \Vert \phi (\mathbf{I}{)}^{\prime }-1_{K_{N\ast q}}\Vert \right)\right)$$

作业day-2

1、令 A = { 1 , 2 , 5 , 8 , 9 } \mathbf{A}=\{1,2,5,8,9\} A={1,2,5,8,9}，写出 $\mathbf{A}$ 上的 “模 2 同余” 关系及相应的划分
R = { ( 1 , 1 ) , ( 1 , 5 ) , ( 1 , 9 ) , ( 2 , 2 ) , ( 2 , 8 ) , ( 5 , 1 ) , ( 5 , 5 ) , ( 5 , 9 ) , ( 8 , 2 ) , ( 8 , 8 ) , ( 9 , 1 ) , ( 9 , 5 ) , ( 9 , 9 ) } \mathbf{R}=\{(1,1),(1,5),(1,9),(2,2),(2,8),(5,1),(5,5),(5,9),(8,2),(8,8),(9,1),(9,5),(9,9)\} R={(1,1),(1,5),(1,9),(2,2),(2,8),(5,1),(5,5),(5,9),(8,2),(8,8),(9,1),(9,5),(9,9)}
P = { { 1 , 5 , 9 } , { 2 , 8 } } \mathcal{P}=\{\{1,5,9\},\{2,8\}\} P={{1,5,9},{2,8}}
2、令 A = { 1 , 2 , 5 , 8 , 9 } \mathbf{A}=\{1,2,5,8,9\} A={1,2,5,8,9}， 自己给定两个关系 ${\mathbf{R}}_1$和 ${\mathbf{R}}_2$
并计算 ${\mathbf{R}}_1\circ {\mathbf{R}}_2$, ${\mathbf{R}}_1^{+}$与${\mathbf{R}}_1^{\ast }$
R 1 = { ( a , b ) ∈ A × A ∣ a / 2 = b / 2 } = { ( 2 , 2 ) , ( 2 , 8 ) , ( 8 , 2 ) , ( 8 , 8 ) } \mathbf{R}_1=\{(a, b) \in \mathbf{A} \times \mathbf{A} \mid a / 2=b / 2\}=\{(2,2),(2,8),(8,2),(8,8)\} R1​={(a,b)∈A×A∣a/2=b/2}={(2,2),(2,8),(8,2),(8,8)}
R 1 = { ( a , b ) ∈ A × A ∣ a m o d    3 = b m o d    3 } = { ( 2 , 2 ) , ( 2 , 5 ) , ( 2 , 8 ) , ( 5 , 2 ) , ( 5 , 5 ) , ( 5 , 8 ) , ( 8 , 2 ) , ( 8 , 5 ) , ( 8 , 8 ) } \mathbf{R}_1=\{(a, b) \in \mathbf{A} \times \mathbf{A} \mid a \mod 3 =b \mod 3\}=\{(2,2),(2,5),(2,8),(5,2),(5,5),(5,8),(8,2),(8,5),(8,8)\} R1​={(a,b)∈A×A∣amod3=bmod3}={(2,2),(2,5),(2,8),(5,2),(5,5),(5,8),(8,2),(8,5),(8,8)}
R 1 + = ⋃ i = 1 ∣ A ∣ R i = R 1 ∪ R 2 ∪ R 3 ∪ R 4 ∪ R 5 = { ( 2 , 2 ) , ( 2 , 8 ) , ( 8 , 8 ) } \mathbf{R}_1^+=\bigcup_{i=1}^{|\mathbf{A}|} \mathbf{R}^{i}=\mathbf{R}^{1} \cup \mathbf{R}^{2} \cup \mathbf{R}^{3} \cup \mathbf{R}^{4} \cup \mathbf{R}^{5}=\{(2,2),(2,8),(8,8)\} R1+​=⋃i=1∣A∣​Ri=R1∪R2∪R3∪R4∪R5={(2,2),(2,8),(8,8)}
R 1 ∗ = R 1 + ∪ R 0 = { ( 2 , 2 ) , ( 2 , 8 ) , ( 8 , 8 ) } \mathbf{R}_1^*=\mathbf{R}_1^+\cup \mathbf{R}^0=\{(2,2),(2,8),(8,8)\} R1∗​=R1+​∪R0={(2,2),(2,8),(8,8)}

4、给定一个矩阵并计算其各种范数
给定矩阵$\mathbf{X}=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$
$l_0=||\mathbf{X}|{|}_0=4$;
$l_1=||\mathbf{X}|{|}_1=1+2+3+4=10$;
$l_2=||\mathbf{X}|{|}_2=\sqrt{1^2+2^2+3^2+4^2}=\sqrt{30}$;
$l_{\infty }=||\mathbf{X}|{|}_{\infty }=4$;

4、解释优化目标式子：
$$\min \sum _{(i,j）\in \Omega }(f({\mathbf{x}}_i,{\mathbf{t}}_j)-r_{ij})\text{\hspace{1em}(1)}$$
式中：
$\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n]$表示用户信息；
$\mathbf{T}=[{\mathbf{t}}_1,\dots ,{\mathbf{t}}_n]$表示商品信息；
$r_{ij}$表示评分矩阵 $\mathbf{R}=(r_{ij}{)}_{n\times m}$中具体的某个评分；
$\Omega$ 为评分矩阵$\mathbf{R}$中非零元素对应位置的集合;
​ $f$目标函数分别通过用户和商品的属性生成一个评分结果；
该式要学习一个 $f$ 用于商品的推荐，使得预测结果$f({\mathbf{x}}_i,{\mathbf{t}}_j)$与真实值$r_{ij}$均方误差MSE最小。

作业day-3

1、将向量$(x_2,x_4,\dots )$累加写出表达式
$y={\sum }_{i=1}^{\lfloor n/2\rfloor }{x}_{2i}$； code：y=\sum_{i=1}^{n}x_{2i}

2、各出一道累加、累乘、积分表达式的习题, 并给出标准答案
累加：$y={\sum }_{i=1}^{100}i=5050$
累乘：$y={\prod }_{i=1}^{5}0.5\times x_i=3.75$
定积分：$y={\int }_2^{5}2x\mathrm{d}x=21$

3、你使用过三重累加吗? 描述一下其应用
弗洛伊德算法，寻找两点之间最短路径，其时间复杂度为$O(n^3)$

（4）给一个常用的定积分, 将手算结果与程序结果对比.
给定定积分：$y={\int }_2^{5}2x\mathrm{d}x$
手算：$y={\int }_2^{5}2x\mathrm{d}x=x^2{|}_2^5=25-4=21$
代码：

import numpy as np
delta=0.01
sumValue=0.0
for i in np.arange(2.0,5.0,delta):
    sumValue+=2*i*delta
print (sumValue)

运算结果：20.96999999999981

4、自己写一个小例子$(n=3,m=1)$来验证最小二乘法
样例：
$\mathbf{X}=\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$
$\mathbf{Y}=\left[\begin{array}{ccc}-1& 3& 4\end{array}\right]$
$\mathbf{w}=({\mathbf{X}}^{\mathrm{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}={\left(\left[\begin{array}{ccc}1& 2& 3\\ 1& 1& 1\end{array}\right]\left[\begin{array}{cc}1& 1\\ 2& 1\\ 3& 1\end{array}\right]\right)}^{-1}\left[\begin{array}{ccc}1& 2& 3\\ 1& 1& 1\end{array}\right]\left[\begin{array}{c}-1\\ 3\\ 4\end{array}\right]=\left[\begin{array}{c}2.5\\ -3\end{array}\right]$
最终答案： $y=2.5x-3$

5、岭回归推导
$$\begin{gathered} L(\mathbf{w})=\underset{\mathbf{w}}{\mathrm{argmin}}\Vert \mathbf{X}\mathbf{w}-\mathbf{Y}{\Vert }_2^2+\lambda \Vert \mathbf{w}{\Vert }_2^2==(\mathbf{X}\mathbf{w}-\mathbf{Y}{)}^{\mathrm{T}}(\mathbf{X}\mathbf{w}-\mathbf{Y})+\lambda {\mathbf{w}}^{\mathrm{T}}\mathbf{w} \\ =\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}-{\mathbf{Y}}^{\mathrm{T}}\right)(\mathbf{X}\mathbf{w}-\mathbf{Y})+\lambda {\mathbf{w}}^{\mathrm{T}}\mathbf{w} \\ ={\mathbf{w}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\mathbf{w}-{\mathbf{w}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}-{\mathbf{Y}}^{\mathrm{T}}\mathbf{X}\mathbf{w}+{\mathbf{Y}}^{\mathrm{T}}\mathbf{Y}+\lambda {\mathbf{w}}^{\mathrm{T}}\mathbf{w} \end{gathered}$$
对$\mathbf{w}$求导有：
$\frac{\partial L(w)}{\partial w}=2{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\mathbf{w}-{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}-{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}+2\lambda \mathbf{w}$
令$\frac{\partial L(w)}{\partial w}=0$可得：
${\mathbf{X}}^{\mathrm{T}}\mathbf{X}\mathbf{w}-{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}+\lambda \mathbf{w}=0$

作业3 逻辑回归推导

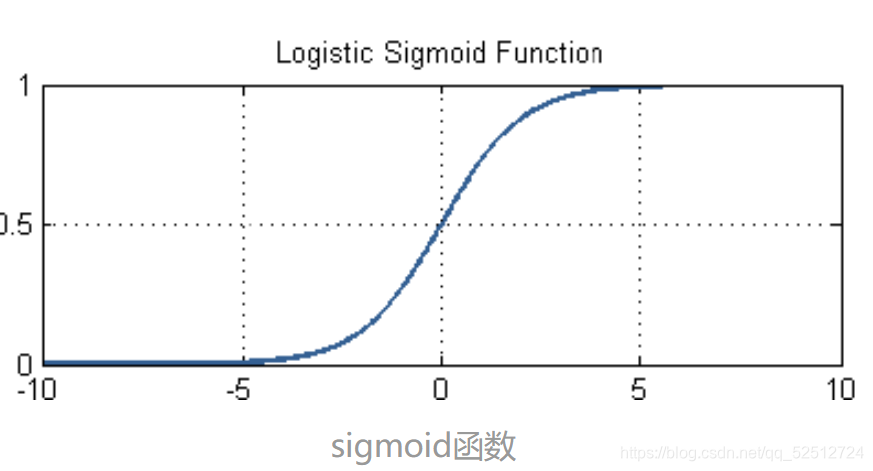
技术1:将线性回归映射到$[0,1]$——sigmoid函数$\sigma (x)=\frac{1}{1+e^{-x}}$

令$\mathbf{x}={\mathbf{w}}^{\mathrm{T}}\mathbf{x}$，则逻辑回归模型为：
$$y=\sigma (f(\mathbf{x}))=\sigma \left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}\right)=\frac{1}{1+e^{-{\mathbf{w}}^{\mathrm{T}}\mathbf{x}}}\text{\hspace{1em}(1)}$$
技术2：利用对数对数降低损失函数的计算难度
令标签为1的概率为p：
$$P_{y=1}=\frac{1}{1+e^{-{\mathbf{w}}^{\mathrm{T}}\mathbf{x}}}=p\text{\hspace{1em}(2)}$$
标签为0的概率为$P_{y=0}=1-p$，则第i个样本的概率为：
$$P\left(y_i\mid {\mathbf{x}}_i\right)=p^{y_i}(1-p{)}^{1-y_i}\text{\hspace{1em}(3)}$$
对于n个样本 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) … ( x n , y n ) } \left\{\left(\mathbf{x}_{1}, y_{1}\right),\left(\mathbf{x}_{2}, y_{2}\right),\left(\mathbf{x}_{3}, y_{3}\right) \ldots\left(\mathbf{x}_{n}, y_{n}\right)\right\} {(x1​,y1​),(x2​,y2​),(x3​,y3​)…(xn​,yn​)}其概率为：
$$\begin{array}{rl}{P}_{\text{总 }}& =P\left(y_1\mid {\mathbf{x}}_1\right)P\left(y_2\mid {\mathbf{x}}_2\right)P\left(y_3\mid {\mathbf{x}}_3\right)\dots P\left(y_n\mid {\mathbf{x}}_n\right)\\ & =\prod _{i=1}^n{p}^{y_i}(1-p{)}^{1-y_i}\end{array}\text{\hspace{1em}(4)}$$
对其求对数不改变其单调性，有损失函数：
$$\begin{array}{rl}L(\mathbf{w})=\ln \left(P_{\text{总 }}\right)& =\ln \left(\prod _{n=1}^N{p}^{y_n}(1-p{)}^{1-y_n}\right)\\ & =\sum _{n=1}^N\ln \left(p^{y_n}(1-p{)}^{1-y_n}\right)\\ & =\sum _{n=1}^N\left(y_n\ln (p)+\left(1-y_n\right)\ln (1-p)\right)\end{array}\text{\hspace{1em}(5)}$$
此刻，只需要找到一个${\mathbf{w}}^{\ast }$使概率最大，则有：
$${\mathbf{w}}^{\ast }=\arg \underset{\mathbf{w}}{\max }L(\mathbf{w})=-\arg \underset{\mathbf{w}}{\min }L(\mathbf{w})\text{\hspace{1em}(6)}$$
技术3：梯度下降求解无解析解的情况
式（2）对p求导，可得
$$\begin{array}{rl}{p}^{\prime }=f^{\prime }(\mathbf{w})& ={\left(\frac{1}{1+e^{-{\mathbf{w}}^{\mathrm{T}}\mathbf{w}}}\right)}^{\prime }\\ & =\frac{1}{1+e^{-{\mathbf{w}}^{\mathrm{T}}\mathbf{x}}}\cdot \frac{e^{-{\mathbf{w}}^{\mathrm{T}}\mathbf{x}}}{1+e^{-{\mathbf{w}}^{\mathrm{T}}\mathbf{x}}}\cdot \mathbf{x}\\ & =p(1-p)\mathbf{x}\end{array}\text{\hspace{1em}(7)}$$
对（5）关于$\mathbf{w}$ 求导有：
$$\begin{array}{rl}\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}=& =\sum _{i=1}^n\left(y_i{\ln }^{\prime }(p)+\left(1-y_i\right){\ln }^{\prime }(1-p)\right)\\ & =\sum _{i=1}^n\left(\left(y_i\frac{1}{p}{p}^{\prime }\right)+\left(1-y_i\right)\frac{1}{1-p}(1-p{)}^{\prime }\right)\\ & =\sum _{i=1}^n\left(y_i(1-p){\mathbf{x}}_i-\left(1-y_i\right)p{\mathbf{x}}_i\right)\\ & =\sum _{i=1}^n\left(y_i-p\right){\mathbf{x}}_i\end{array}\text{\hspace{1em}(8)}$$
令（8）偏导为0由于无法获得解析式，则借助梯度下降可得模型参数$\mathbf{w}$更新式子：
$${\mathbf{w}}^{t+1}={\mathbf{w}}^{\mathrm{T}}-\alpha \frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}\text{\hspace{1em}(9)}$$

逻辑回归的特点：
（1）使用sigmoid函数映射线性回归到$[0,1]$区间；
（2）使用概率将回归问题变成分类问题；
（3）使用对数函数降低计算难度；
（4）使用梯度下降在无法获得解析式的情况下求解模型参数；
（5）不能用Logistic回归去解决非线性问题，因为Logistic的决策面为线性面。

作业day-4

1、无向图定义
Definition :An undirected network is a tuple $N=(\mathbf{V},\mathbf{E},\mathbf{W})$,where $\mathbf{V}$ is the set of nodes,$\mathbf{E}\subseteq V\times V$ where $(v_i,v_j)\in \mathbf{E}\iff (v_j,v_i)\in \mathbf{E}$ is the set of nodes, $w\in \mathbf{W}$ is the weighted of $(v_i,v_j)$.

2、树的定义

（1）自己画一棵树, 将其元组各部分写出来 (特别是函数$p$).
Let $\varphi$ be the empty node, a tree is a triple $T=(\mathbf{A},{\mathrm{A}}_0,\mathrm{p})$ where
∙ A = { A 0 , A 1 , … , A 6 } ≠ ϕ \bull \mathbf{A} =\{\rm A_0, \rm A_1, \dots, \rm A_6\}\neq\phi ∙A={A0​,A1​,…,A6​}​=ϕ is the set of nodes;
$\bullet {\mathrm{A}}_0\in \mathbf{A}$ is the root node;
∙ p : A → A ∪ { ϕ } \bull p: \mathbf{A} \to\mathbf{A} \cup\{\phi\} ∙p:A→A∪{ϕ} is the parent mapping satisfying;
   $:p(A_0)=\varphi$
   $:\forall \mathrm{A}\in \mathbf{A},\exists 1\mathrm{n}\ge 0,\text{ s.t. }{\mathrm{p}}^{(\mathrm{n})}(\mathrm{A})={\mathrm{A}}_0$
(2)针对该树, 将代码中的变量值写出来
code:

public class Tree {
	/**
	 * 节点数. 表示节点 v_0 至 v_{n-1}.
	 */
	int n;
	
	/**
	 * 根节点. 0 至 n-1.
	 */
	int root;
	
	/**
	 * 父节点.
	 */
	int[] parent;

	/**
	 * 构造一棵树, 第一个节点为根节点, 其余节点均为其直接子节点, 也均为叶节点.
	 */
	public Tree(int paraN) {
		n = paraN;
		parent = new int[n];
		parent[0] = -1; // -1 即 \phi
	}// Of the constructor
}//Of class Tree

其中：
n=6；root=0；
parent[0]=-1; parent[1]=0; parent[2]=0; parent[3]=1; parent[4]=1; parent[5]=2; parent[6]=2;

3、画一棵三叉树, 并写出它的 child 数组

child： { ( 1 , 2 , 3 ) ; ( 4 , − 1 , 5 ) ; ( − 1 , − 1 , 6 ) ; ( − 1 , − 1 , − 1 ) ; ( − 1 , − 1 , − 1 ) ; ( − 1 , − 1 , − 1 ) ; ( − 1 , − 1 , − 1 ) } \{(1, 2, 3) ;(4, -1, 5) ;(-1, -1, 6) ;(-1, -1,-1) ;(-1,-1,-1) ;(-1,-1,-1) ;(-1,-1,-1)\} {(1,2,3);(4,−1,5);(−1,−1,6);(−1,−1,−1);(−1,−1,−1);(−1,−1,−1);(−1,−1,−1)}

4、重新定义树
Let $\varphi$ be the empty node, a tree is a triple $T=(\mathbf{A},{\mathrm{A}}_0,\mathrm{\Sigma },\mathrm{c})$ where
∙ A = { A 0 , A 1 , … , A 6 } ≠ ϕ \bull \mathbf{A} =\{ \rm A_0, \rm A_1, \dots,\rm A_6\}\neq\phi ∙A={A0​,A1​,…,A6​}​=ϕ is the set of nodes;
$\bullet {\mathrm{A}}_0\in \mathbf{A}$ is the root node;
∙ Σ = { 0 , … , 6 } \bull \Sigma =\{0,\dots,6\} ∙Σ={0,…,6} is the alphabet;
∙ c : ( A ∪ { ϕ } ) × Σ ∗ → A ∪ { ϕ } \bull c:(\mathbf{A} \cup\{\phi\}) \times \Sigma^{*} \rightarrow \mathbf{A} \cup\{\phi\} ∙c:(A∪{ϕ})×Σ∗→A∪{ϕ} satisfying ;
   $\bullet \forall \mathrm{A}\in \mathbf{A},\exists 1\mathrm{s}\in {\mathrm{\Sigma }}^{\ast }\text{ s.t. }\mathrm{c}(\mathrm{r},\mathrm{s})=\mathrm{A}$

作业day-5

1、定义一个标签分布系统, 即各标签的值不是 0/1，而是 $[0,1]$ 区间的实数，且同一对象的标签和为1
A label distribution learning is a tuple $S=(\mathbf{X},\mathbf{Y})$ where $\mathbf{X}=[x_{ij}{]}_{n\times m}\in {\mathbb{R}}^{n\times m}$ is the data matrix, $\mathbf{Y}=[y_{ik}{]}_{n\times l}\in [0,1{]}^{n\times l}$ is the label matrix, s.t. ${\sum }_{t=1}^k{y}_{ik}=1$, $n$ is the number of instances, $m$ is the number of features, and $l$ is the number of labels.

2、 找一篇你们小组的论文来详细分析数学表达式, 包括其涵义, 规范, 优点和缺点.
数学表达式：
$$\underset{{\mathbf{v}}^{(j)}}{\min }E\left({\mathbf{v}}^{(j)}\right)=\sum _{i=1}^{l}L\left(y_i,g^{(j)}({\mathbf{x}}_i)\right)+\sum _{i=l+1}^{l+u}{v}_i^{(j)}L\left({\overline{g}}^{(j-1)}({\mathbf{x}}_i),g^{(j)}({\mathbf{x}}_i)\right)\text{\hspace{1em}(10)}$$
涵义：在第$j$个视角上，在输入为${\mathbf{v}}^{(j)}$的情况下，使模型在标记数据与伪标记数据上的预测损失最小。
优点：简介明了，变量名未出现混用的情况。
缺点：无法一次性讲整个多个视角之间的优化情况写出。