目录
掌握关系的定义(集合中元素之间的关系)
掌握关系的表示
掌握关系的性质
4.1 二元关系及其表示
1)当元素x关于元素y具有指定的关系R时—>xRy(笛卡尔序偶(x,y))
2)当元素x关于元素y不具有指定的关系R时—>xy
※R是A×B的一个合于R={(x,y)A×B}的子集合
xRy<=>(x,y)R
定义:A×B的子集和A×B自身是A到B的两个二元关系,分别称为空关系和全关系。
※关系图法(有向图表示法)
关系矩阵表示法:(布尔矩阵/邻接矩阵)
注意:在写关系矩阵时,首先应对集合A和B中的元素进行排序!
4.2 关系的性质
1.自反性与反自反性
2.对称性与反对称性(不是绝对对立的)
3.传递性
4.3 关系的运算
4.3.1 关系的交、并、补、差集
eg.
{(x,y)|(xRy)
(xSy)}
异或
4.3.2 关系的复合运算
定义:R1 ◦ R2={(x,z)|(xA)
(z
C)
((y
B)
(xRy)
(ySz))}
R:A—>B,S:B—>C,R1 ◦ R2是从A到C的关系
4.3.3 关系的幂
1.
{
}
2.
3.
◦ R=R◦
!!
◦
=
,
=
4.3.4 关系的逆运算
定义:={(b,a)|(a,b)
R}
※和
是完全不同的两种关系
4.3.5 关系运算的性质
1)(R◦S)◦T=R◦(S◦T)
2)(R◦=
◦
定理1:eg. R◦=(R◦S)
(R◦T)
定理2:① ②
4.4 二元关系的闭包
闭包即为满足条件的最小二元关系。
1)自反闭包——>r(R)
2)对称闭包——>s(R)
3)传递闭包——>t(R)
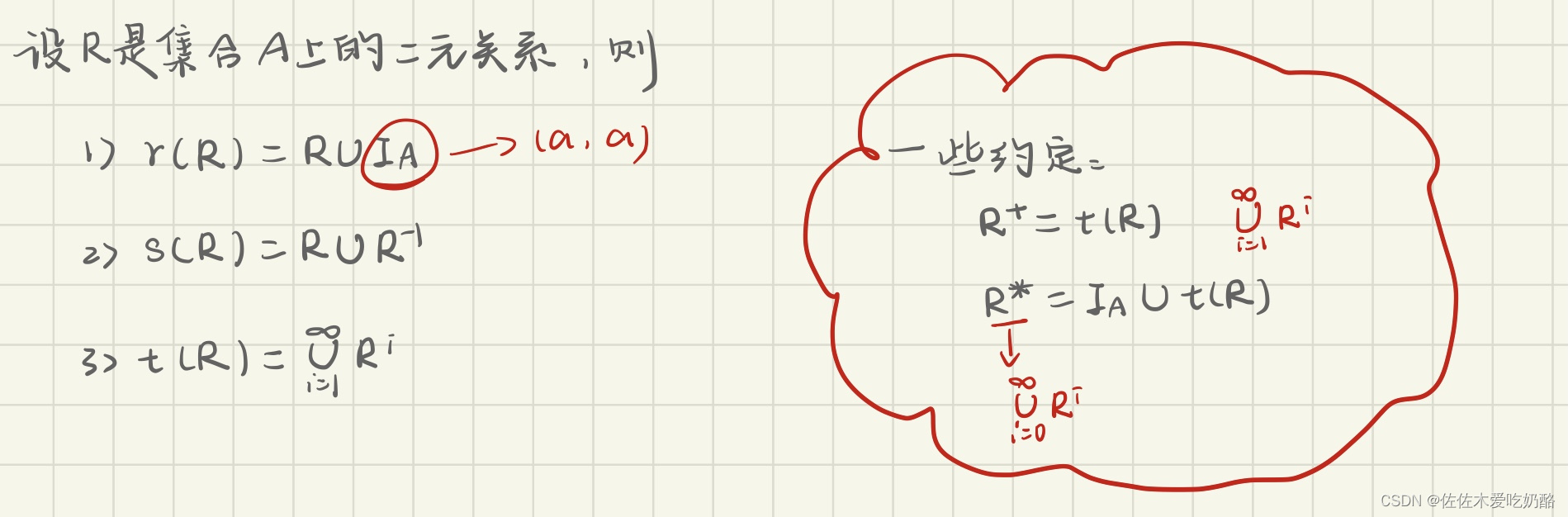
重点:Warshall算法——>求传递闭包
步骤1:每一列中元素从上到下扫描
步骤2:若当前扫描的是第i列,那么当遇到1时,将所对应的行加上第i行
4.4.1 闭包运算的性质
※若R是传递的,则r(R)也是传递的
1)rs(R)=SR(R)
2)rt(R)=tr(R)
3)st(R)≤ts(R)








 本文深入探讨了关系代数的基础概念,包括二元关系的表示方法、关系的性质(如自反性、对称性和传递性)、关系的运算(交、并、补、差集、复合、幂和逆运算)以及闭包运算。特别是重点介绍了关系的闭包运算,包括自反闭包、对称闭包和传递闭包,并提到了Warshall算法在求传递闭包中的应用。此外,还讨论了关系运算的一些基本性质和定理。
本文深入探讨了关系代数的基础概念,包括二元关系的表示方法、关系的性质(如自反性、对称性和传递性)、关系的运算(交、并、补、差集、复合、幂和逆运算)以及闭包运算。特别是重点介绍了关系的闭包运算,包括自反闭包、对称闭包和传递闭包,并提到了Warshall算法在求传递闭包中的应用。此外,还讨论了关系运算的一些基本性质和定理。




















 4613
4613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








