核函数（高斯核函数）

核函数的目的

核函数包括

①高斯核函数②多项式核函数③核函数④线性核函数

核函数的出发点

       让机器进行建模的时候传进来的数据更丰富一些，信息更多一些，让机器更好去理解；核函数相当于把低维的数据通过某种方法或形式转换成一个高维的数据。

       还是用XOR Problem来举例，XOR Problem在FNN中提起过。将非线性问题利用升维转换为一个线性问题。

高斯核函数

       不难发现，高斯就是我们平常学过的正态分布。

       x，y是函数中随便的两个样本点，代表的就是数据，是一个特征。x-y可以理解为样本点相减，其实就是在计算样本间的一个差异性，表示两个样本点的一个相似性，如果x和y很相似，则K=eº=1；反之，若很不相似，则K=e-∞=0，说明x和y的差异性巨大。σ²还是指方差。

       所以这样做有什么好处?可以给我们带来什么？

       越多的特征，得到的结果越复杂，处理问题的能力就越强，随之风险也就越大；可以给我们带来无穷维的一个特征。

       来看推导过程：

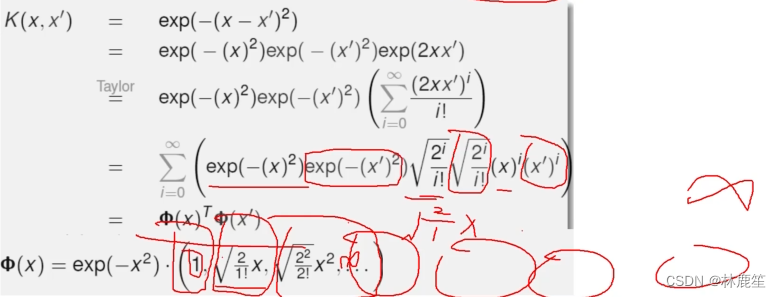
       特别的，在φ(x)中，exp(-x^2)是常数项，决定特征维数的正式后面的展开式。

参数的影响

       假设有m个数据，根据前面提到的exp||X-Y||²，我们可以计算出（x_i,x_1）,（x_i,x_2）,……,（x_i,x_m）,根据exp||X-Y||²可以得到特征feature分别为F_1,F_2,……F_m，我们将这些feature做成向量，可以得到X_i的特征向量（F_1,F_2,……F_m），无论X_i是多少维的特征都会被变为m维，这就是高斯函数。

高斯核函数对参数很敏感

       看起来不错，但是它对参数是极其敏感的，效果差异也是很大的。

       σ越小→图像越尖锐→度量变化的越快→棱次更分明→特征更鲜明

       σ越大→图像越平缓→度量变化的平缓→棱次不分明→特征变化的幅度小

参数对决策边界的影响

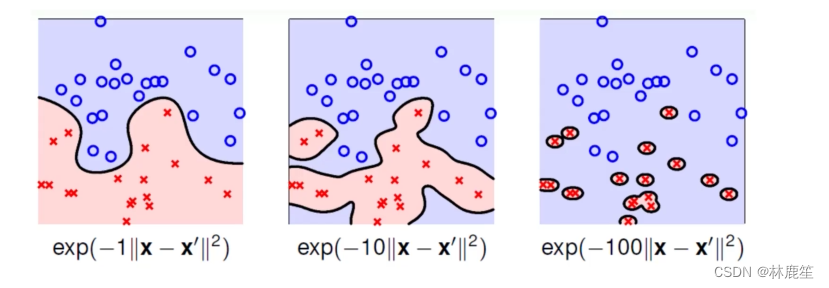
       σ越小→切分越厉害→越容易过拟合

总结

       核函数最基本的出发点：升维，升维的目的：使数据或者决策边界的信息更多一些，能做的更好一些。

线性核函数

       Linear核函数对数据不做任何变换，什么参数都不用直接拿去做就好。

       一般任务来的时候，先用线性函数做一个变换，看一下效果如何。